On this page
Three Point Molly
Introduction
The Three Point Molly is a betting system based on craps. There is no easy way to implement it on other games. The concept is simple -- The player keeps making pass or come bets until he has at least three, backing them up with full odds.
Using the Three Point Molly will give the player a house advantage under 0.5%, which is very good. It doesn't achieve this via the betting system, but because the player is making very good bets to begin with. I used to play this system, not knowing there was a name for it at the time.
Rules
The following rules understand the player knows the rules of craps. If you don't, please at least review the rules of the pass, come, and odds bets in craps before going further.
Here is the short version of how to play the Three Point Molly. Make a pass or come bet every roll, until you have three numbers covered. Back up all pass and come bets with the odds, preferably the maximum multiple allowed.
Next, here is the longer version of how to play the Three Point Molly.
The player will have to decide how much money a betting unit is. For example $10. It will have to at least be the minimum pass line bet. Every pass or come bet will be for one unit.
- If it is a come out roll and the player has less than three numbers covered, then make a pass line bet.
- If it is not a come out roll and the player has less than three numbers covered, then make a come bet.
- If three numbers are already covered, then don't make any new bets.
- If a pass or come bet was made the previous roll and a point number (4, 5, 6, 8, 9, or 10) was rolled, then back it up with the odds, preferably the maximum allowed.
- On a come out roll, turn off the odds on any outstanding come bets.
- Keep repeating the four steps above until a seven-out, which marks the end of the session.
Analysis
To analyze the Three Point Molly, I ran through over 32 billion sessions playing it via computer simulation. I assumed the player always took full 3-4-5x odds. Here are some statistics about what to expect per session, defined as playing until the shooter sevens-out.
- Average units bet: 21.318409
- Averages units won: -0.086295
- Ratio money won to money bet = -0.004048
- Average dice rolls = 8.525470
- Probability session win = 0.304783
- Average units won, given a win = 15.880052
- Probability session loss = 0.673288
- Average units lost, given a loss = 7.316730
- Probability session push = 0.021929
- Net points won (not counting come bets on a come out roll) = -0.688804
- Probability losing three points (not counting come bets on a come out roll) = 0.114039
The spoiler box below shows the raw results of the count of each net win in the simulation.
Simulation Results — Net Units Won
| Net Win | Count | Probability |
|---|---|---|
| -28 | 2 | 0.000000 |
| -27 | 7 | 0.000000 |
| -26 | 63 | 0.000000 |
| -25 | 412 | 0.000000 |
| -24 | 2,867 | 0.000000 |
| -23 | 20,077 | 0.000001 |
| -22 | 134,791 | 0.000004 |
| -21 | 869,965 | 0.000027 |
| -20 | 5,283,822 | 0.000163 |
| -19 | 29,276,571 | 0.000905 |
| -18 | 140,054,558 | 0.004330 |
| -17 | 505,734,437 | 0.015637 |
| -16 | 847,665,043 | 0.026209 |
| -15 | 1,070,934,993 | 0.033112 |
| -14 | 670,280,254 | 0.020724 |
| -13 | 352,443,711 | 0.010897 |
| -12 | 278,945,010 | 0.008625 |
| -11 | 739,681,501 | 0.022870 |
| -10 | 1,595,074,146 | 0.049318 |
| -9 | 1,923,363,355 | 0.059469 |
| -8 | 1,717,525,038 | 0.053104 |
| -7 | 1,009,831,502 | 0.031223 |
| -6 | 860,061,437 | 0.026592 |
| -5 | 2,273,628,075 | 0.070298 |
| -4 | 2,532,516,176 | 0.078303 |
| -3 | 2,453,703,762 | 0.075866 |
| -2 | 1,590,852,863 | 0.049188 |
| -1 | 1,177,924,337 | 0.036420 |
| 0 | 709,247,041 | 0.021929 |
| 1 | 418,005,746 | 0.012924 |
| 2 | 348,914,435 | 0.010788 |
| 3 | 474,520,818 | 0.014672 |
| 4 | 659,962,642 | 0.020405 |
| 5 | 746,209,688 | 0.023072 |
| 6 | 670,131,253 | 0.020720 |
| 7 | 453,417,199 | 0.014019 |
| 8 | 281,844,697 | 0.008714 |
| 9 | 217,130,866 | 0.006713 |
| 10 | 261,596,855 | 0.008088 |
| 11 | 365,365,278 | 0.011297 |
| 12 | 431,269,636 | 0.013334 |
| 13 | 402,459,901 | 0.012444 |
| 14 | 290,068,463 | 0.008969 |
| 15 | 190,356,909 | 0.005886 |
| 16 | 148,875,109 | 0.004603 |
| 17 | 168,971,362 | 0.005224 |
| 18 | 222,536,389 | 0.006881 |
| 19 | 258,730,303 | 0.008000 |
| 20 | 243,848,069 | 0.007540 |
| 21 | 183,847,545 | 0.005684 |
| 22 | 126,712,604 | 0.003918 |
| 23 | 100,938,946 | 0.003121 |
| 24 | 109,853,273 | 0.003397 |
| 25 | 137,408,404 | 0.004249 |
| 26 | 156,412,528 | 0.004836 |
| 27 | 148,145,000 | 0.004581 |
| 28 | 115,654,061 | 0.003576 |
| 29 | 83,203,562 | 0.002573 |
| 30 | 67,504,800 | 0.002087 |
| 31 | 71,149,502 | 0.002200 |
| 32 | 85,219,705 | 0.002635 |
| 33 | 94,997,541 | 0.002937 |
| 34 | 90,199,021 | 0.002789 |
| 35 | 72,437,048 | 0.002240 |
| 36 | 54,084,552 | 0.001672 |
| 37 | 44,653,965 | 0.001381 |
| 38 | 45,923,694 | 0.001420 |
| 39 | 53,009,464 | 0.001639 |
| 40 | 57,913,108 | 0.001791 |
| 41 | 55,062,481 | 0.001702 |
| 42 | 45,282,109 | 0.001400 |
| 43 | 34,900,804 | 0.001079 |
| 44 | 29,257,203 | 0.000905 |
| 45 | 29,511,169 | 0.000912 |
| 46 | 33,021,850 | 0.001021 |
| 47 | 35,422,854 | 0.001095 |
| 48 | 33,711,968 | 0.001042 |
| 49 | 28,262,050 | 0.000874 |
| 50 | 22,384,612 | 0.000692 |
| 51 | 19,029,160 | 0.000588 |
| 52 | 18,910,013 | 0.000585 |
| 53 | 20,611,313 | 0.000637 |
| 54 | 21,741,065 | 0.000672 |
| 55 | 20,686,720 | 0.000640 |
| 56 | 17,631,119 | 0.000545 |
| 57 | 14,301,005 | 0.000442 |
| 58 | 12,314,655 | 0.000381 |
| 59 | 12,080,858 | 0.000374 |
| 60 | 12,871,214 | 0.000398 |
| 61 | 13,380,196 | 0.000414 |
| 62 | 12,720,728 | 0.000393 |
| 63 | 10,996,692 | 0.000340 |
| 64 | 9,105,439 | 0.000282 |
| 65 | 7,922,403 | 0.000245 |
| 66 | 7,700,089 | 0.000238 |
| 67 | 8,043,796 | 0.000249 |
| 68 | 8,255,742 | 0.000255 |
| 69 | 7,848,058 | 0.000243 |
| 70 | 6,865,255 | 0.000212 |
| 71 | 5,783,499 | 0.000179 |
| 72 | 5,078,376 | 0.000157 |
| 73 | 4,898,927 | 0.000151 |
| 74 | 5,034,619 | 0.000156 |
| 75 | 5,103,691 | 0.000158 |
| 76 | 4,847,033 | 0.000150 |
| 77 | 4,283,029 | 0.000132 |
| 78 | 3,660,754 | 0.000113 |
| 79 | 3,238,821 | 0.000100 |
| 80 | 3,108,409 | 0.000096 |
| 81 | 3,150,362 | 0.000097 |
| 82 | 3,165,959 | 0.000098 |
| 83 | 2,999,627 | 0.000093 |
| 84 | 2,674,553 | 0.000083 |
| 85 | 2,311,446 | 0.000071 |
| 86 | 2,062,521 | 0.000064 |
| 87 | 1,970,926 | 0.000061 |
| 88 | 1,973,623 | 0.000061 |
| 89 | 1,965,000 | 0.000061 |
| 90 | 1,861,453 | 0.000058 |
| 91 | 1,670,294 | 0.000052 |
| 92 | 1,461,087 | 0.000045 |
| 93 | 1,310,897 | 0.000041 |
| 94 | 1,247,190 | 0.000039 |
| 95 | 1,234,522 | 0.000038 |
| 96 | 1,220,060 | 0.000038 |
| 97 | 1,154,054 | 0.000036 |
| 98 | 1,044,137 | 0.000032 |
| 99 | 920,394 | 0.000028 |
| 100 | 832,175 | 0.000026 |
| 101 | 787,011 | 0.000024 |
| 102 | 773,880 | 0.000024 |
| 103 | 757,517 | 0.000023 |
| 104 | 718,633 | 0.000022 |
| 105 | 653,186 | 0.000020 |
| 106 | 580,952 | 0.000018 |
| 107 | 525,360 | 0.000016 |
| 108 | 497,143 | 0.000015 |
| 109 | 484,725 | 0.000015 |
| 110 | 472,951 | 0.000015 |
| 111 | 445,616 | 0.000014 |
| 112 | 407,531 | 0.000013 |
| 113 | 365,717 | 0.000011 |
| 114 | 332,604 | 0.000010 |
| 115 | 313,971 | 0.000010 |
| 116 | 304,434 | 0.000009 |
| 117 | 295,887 | 0.000009 |
| 118 | 278,744 | 0.000009 |
| 119 | 255,852 | 0.000008 |
| 120 | 230,156 | 0.000007 |
| 121 | 210,020 | 0.000006 |
| 122 | 198,054 | 0.000006 |
| 123 | 189,933 | 0.000006 |
| 124 | 183,510 | 0.000006 |
| 125 | 173,189 | 0.000005 |
| 126 | 159,974 | 0.000005 |
| 127 | 144,554 | 0.000004 |
| 128 | 132,215 | 0.000004 |
| 129 | 124,269 | 0.000004 |
| 130 | 119,071 | 0.000004 |
| 131 | 114,510 | 0.000004 |
| 132 | 108,716 | 0.000003 |
| 133 | 100,078 | 0.000003 |
| 134 | 91,216 | 0.000003 |
| 135 | 83,570 | 0.000003 |
| 136 | 78,006 | 0.000002 |
| 137 | 74,593 | 0.000002 |
| 138 | 72,325 | 0.000002 |
| 139 | 67,766 | 0.000002 |
| 140 | 62,234 | 0.000002 |
| 141 | 57,088 | 0.000002 |
| 142 | 52,607 | 0.000002 |
| 143 | 48,854 | 0.000002 |
| 144 | 46,992 | 0.000001 |
| 145 | 44,948 | 0.000001 |
| 146 | 42,257 | 0.000001 |
| 147 | 39,063 | 0.000001 |
| 148 | 35,878 | 0.000001 |
| 149 | 32,842 | 0.000001 |
| 150 | 30,842 | 0.000001 |
| 151 | 29,896 | 0.000001 |
| 152 | 27,741 | 0.000001 |
| 153 | 26,310 | 0.000001 |
| 154 | 24,503 | 0.000001 |
| 155 | 22,429 | 0.000001 |
| 156 | 20,836 | 0.000001 |
| 157 | 19,530 | 0.000001 |
| 158 | 18,360 | 0.000001 |
| 159 | 17,527 | 0.000001 |
| 160 | 16,597 | 0.000001 |
| 161 | 15,348 | 0.000000 |
| 162 | 13,773 | 0.000000 |
| 163 | 13,047 | 0.000000 |
| 164 | 12,509 | 0.000000 |
| 165 | 11,737 | 0.000000 |
| 166 | 10,958 | 0.000000 |
| 167 | 10,199 | 0.000000 |
| 168 | 9,501 | 0.000000 |
| 169 | 8,880 | 0.000000 |
| 170 | 8,396 | 0.000000 |
| 171 | 7,634 | 0.000000 |
| 172 | 7,399 | 0.000000 |
| 173 | 6,839 | 0.000000 |
| 174 | 6,566 | 0.000000 |
| 175 | 6,050 | 0.000000 |
| 176 | 5,745 | 0.000000 |
| 177 | 5,277 | 0.000000 |
| 178 | 4,783 | 0.000000 |
| 179 | 4,447 | 0.000000 |
| 180 | 4,378 | 0.000000 |
| 181 | 4,001 | 0.000000 |
| 182 | 3,696 | 0.000000 |
| 183 | 3,570 | 0.000000 |
| 184 | 3,243 | 0.000000 |
| 185 | 3,031 | 0.000000 |
| 186 | 2,820 | 0.000000 |
| 187 | 2,688 | 0.000000 |
| 188 | 2,599 | 0.000000 |
| 189 | 2,405 | 0.000000 |
| 190 | 2,228 | 0.000000 |
| 191 | 2,161 | 0.000000 |
| 192 | 1,867 | 0.000000 |
| 193 | 1,756 | 0.000000 |
| 194 | 1,704 | 0.000000 |
| 195 | 1,568 | 0.000000 |
| 196 | 1,439 | 0.000000 |
| 197 | 1,383 | 0.000000 |
| 198 | 1,288 | 0.000000 |
| 199 | 1,210 | 0.000000 |
| 200 | 1,117 | 0.000000 |
| 201 | 1,007 | 0.000000 |
| 202 | 942 | 0.000000 |
| 203 | 917 | 0.000000 |
| 204 | 883 | 0.000000 |
| 205 | 821 | 0.000000 |
| 206 | 719 | 0.000000 |
| 207 | 688 | 0.000000 |
| 208 | 653 | 0.000000 |
| 209 | 612 | 0.000000 |
| 210 | 559 | 0.000000 |
| 211 | 525 | 0.000000 |
| 212 | 511 | 0.000000 |
| 213 | 506 | 0.000000 |
| 214 | 435 | 0.000000 |
| 215 | 395 | 0.000000 |
| 216 | 386 | 0.000000 |
| 217 | 340 | 0.000000 |
| 218 | 336 | 0.000000 |
| 219 | 301 | 0.000000 |
| 220 | 286 | 0.000000 |
| 221 | 277 | 0.000000 |
| 222 | 251 | 0.000000 |
| 223 | 243 | 0.000000 |
| 224 | 228 | 0.000000 |
| 225 | 227 | 0.000000 |
| 226 | 179 | 0.000000 |
| 227 | 180 | 0.000000 |
| 228 | 156 | 0.000000 |
| 229 | 153 | 0.000000 |
| 230 | 142 | 0.000000 |
| 231 | 136 | 0.000000 |
| 232 | 136 | 0.000000 |
| 233 | 130 | 0.000000 |
| 234 | 127 | 0.000000 |
| 235 | 117 | 0.000000 |
| 236 | 113 | 0.000000 |
| 237 | 111 | 0.000000 |
| 238 | 77 | 0.000000 |
| 239 | 99 | 0.000000 |
| 240 | 90 | 0.000000 |
| 241 | 69 | 0.000000 |
| 242 | 74 | 0.000000 |
| 243 | 68 | 0.000000 |
| 244 | 67 | 0.000000 |
| 245 | 55 | 0.000000 |
| 246 | 56 | 0.000000 |
| 247 | 49 | 0.000000 |
| 248 | 50 | 0.000000 |
| 249 | 48 | 0.000000 |
| 250 | 38 | 0.000000 |
| 251 | 37 | 0.000000 |
| 252 | 38 | 0.000000 |
| 253 | 30 | 0.000000 |
| 254 | 23 | 0.000000 |
| 255 | 42 | 0.000000 |
| 256 | 30 | 0.000000 |
| 257 | 16 | 0.000000 |
| 258 | 24 | 0.000000 |
| 259 | 22 | 0.000000 |
| 260 | 15 | 0.000000 |
| 261 | 21 | 0.000000 |
| 262 | 20 | 0.000000 |
| 263 | 16 | 0.000000 |
| 264 | 19 | 0.000000 |
| 265 | 16 | 0.000000 |
| 266 | 10 | 0.000000 |
| 267 | 21 | 0.000000 |
| 268 | 8 | 0.000000 |
| 269 | 16 | 0.000000 |
| 270 | 9 | 0.000000 |
| 271 | 13 | 0.000000 |
| 272 | 8 | 0.000000 |
| 273 | 13 | 0.000000 |
| 274 | 7 | 0.000000 |
| 275 | 4 | 0.000000 |
| 276 | 13 | 0.000000 |
| 277 | 9 | 0.000000 |
| 278 | 5 | 0.000000 |
| 279 | 13 | 0.000000 |
| 280 | 4 | 0.000000 |
| 281 | 4 | 0.000000 |
| 282 | 3 | 0.000000 |
| 283 | 12 | 0.000000 |
| 284 | 6 | 0.000000 |
| 285 | 2 | 0.000000 |
| 286 | 7 | 0.000000 |
| 287 | 2 | 0.000000 |
| 288 | 3 | 0.000000 |
| 290 | 4 | 0.000000 |
| 291 | 1 | 0.000000 |
| 292 | 5 | 0.000000 |
| 294 | 1 | 0.000000 |
| 295 | 2 | 0.000000 |
| 296 | 5 | 0.000000 |
| 297 | 1 | 0.000000 |
| 298 | 1 | 0.000000 |
| 299 | 4 | 0.000000 |
| 300 | 2 | 0.000000 |
| 302 | 4 | 0.000000 |
| 303 | 1 | 0.000000 |
| 305 | 1 | 0.000000 |
| 307 | 1 | 0.000000 |
| 309 | 1 | 0.000000 |
| 310 | 1 | 0.000000 |
| 311 | 1 | 0.000000 |
| 312 | 1 | 0.000000 |
| 313 | 1 | 0.000000 |
| 316 | 1 | 0.000000 |
| 317 | 1 | 0.000000 |
| 318 | 1 | 0.000000 |
| 322 | 1 | 0.000000 |
| 345 | 1 | 0.000000 |
| Total | 32,342,500,000 | 1.000000 |
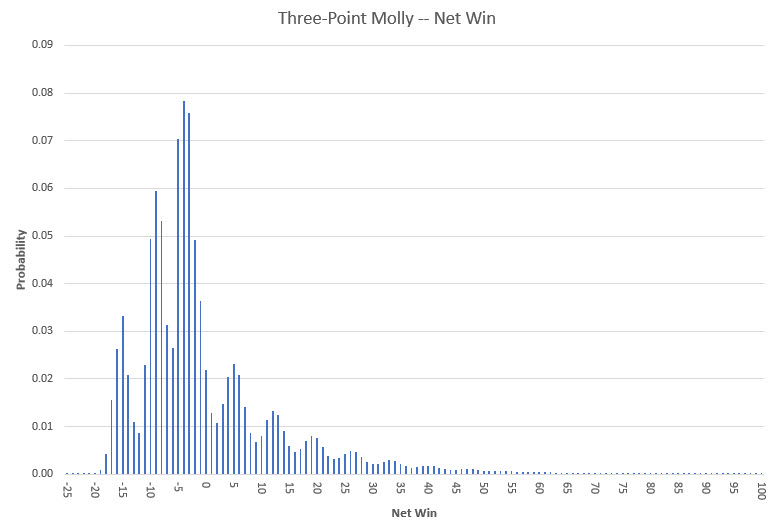
The following chart shows the probability of a net win of -25 to +100 units.
I ran a separate simulation of 7.6 billion sessions that looked at the net points won, not counting wins on a come out roll (because the odds were turned off). The spoiler button below shows the results.
Simulation Results — Net Points Won
| Net Points Won |
Count | Probability |
|---|---|---|
| -3 | 866,696,937 | 0.114039 |
| -2 | 1,799,063,609 | 0.236719 |
| -1 | 2,707,830,104 | 0.356293 |
| 0 | 859,942,908 | 0.113150 |
| 1 | 509,181,625 | 0.066998 |
| 2 | 318,786,035 | 0.041946 |
| 3 | 200,282,777 | 0.026353 |
| 4 | 125,828,052 | 0.016556 |
| 5 | 79,035,018 | 0.010399 |
| 6 | 49,629,205 | 0.006530 |
| 7 | 31,167,223 | 0.004101 |
| 8 | 19,559,543 | 0.002574 |
| 9 | 12,280,517 | 0.001616 |
| 10 | 7,710,235 | 0.001015 |
| 11 | 4,842,391 | 0.000637 |
| 12 | 3,039,626 | 0.000400 |
| 13 | 1,907,701 | 0.000251 |
| 14 | 1,197,193 | 0.000158 |
| 15 | 751,657 | 0.000099 |
| 16 | 471,330 | 0.000062 |
| 17 | 296,874 | 0.000039 |
| 18 | 186,123 | 0.000024 |
| 19 | 116,693 | 0.000015 |
| 20 | 73,449 | 0.000010 |
| 21 | 45,690 | 0.000006 |
| 22 | 28,787 | 0.000004 |
| 23 | 18,141 | 0.000002 |
| 24 | 11,410 | 0.000002 |
| 25 | 7,248 | 0.000001 |
| 26 | 4,395 | 0.000001 |
| 27 | 2,775 | 0.000000 |
| 28 | 1,759 | 0.000000 |
| 29 | 1,081 | 0.000000 |
| 30 | 714 | 0.000000 |
| 31 | 426 | 0.000000 |
| 32 | 276 | 0.000000 |
| 33 | 182 | 0.000000 |
| 34 | 98 | 0.000000 |
| 35 | 69 | 0.000000 |
| 36 | 40 | 0.000000 |
| 37 | 31 | 0.000000 |
| 38 | 20 | 0.000000 |
| 39 | 17 | 0.000000 |
| 40 | 8 | 0.000000 |
| 41 | 2 | 0.000000 |
| 42 | 4 | 0.000000 |
| 43 | 1 | 0.000000 |
| 45 | 1 | 0.000000 |
| Total | 7,600,000,000 | 1.000000 |
Video
Please enjoy my video on the Three Point Molly.
Improving on the Three Point Molly
The player can lower the overall house edge from 0.405% to 0.374% by keeping the odds on a come bet working on a come out roll.
Conclusion
What is important in gambling is the game played, bet made, and sometimes your skill in making decisions. What is not important is the reason for making a bet. For that reason, betting systems are not mathematical voodoo that put the odds in the player's favor. No, not only don't betting systems lower the house edge, they don't even dent it.
The great thing about the Three Point Molly is not the method, but that it's played on very low house edge bets. The pass and come bets carry a 1.41% house edge, while all the odds bets carry a 0.00% house edge. Taking a blended average, the overall house edge is 0.40%. It is hard to beat that in the casino.
Internal Links
Three Point Dolly — The evil twin of the Three Point Molly, based on making don't pass, don't come, and laying the odds. The odds are even better than the Three Point Molly, but you'll have to suffer the stink-eye at the tables.
External Links
Discussion about the Three Point Molly in my forum at Wizard of Vegas.




