Roulette - General Questions
If one bet on two columns in roulette the probability of winning would be 24/38, or 63%. This seems like a winning strategy to me, what is your opinion?
In roulette any bet or combination of bets carries a high house edge. The more likely you are to win the more you will have to risk relative to the reward. If you do this 10 times the probability of showing a profit is 46.42%. At 100 times the probability drops to 24.6%.
I liked your article about the cancellation betting system. What sort of a cancellation system would you follow if instead of betting on either black or red, you placed a bet (of the same amount) on two of the three blocks that cover 12 numbers (e.g: 1 to 12 & 25 to 36) on each roll?
Start the same way as I explained with even money bets. Each bet should be the sum of the left and right numbers. However, following your two column strategy you should add double the amount to the right if you lose.
The www.ccc-casino.com has no-zero roulette, which they call Super Chance Roulette. Are there any systems that would be effective since there is no zero? Without the zero could one effectively play both black and red at the same time, since there is no fear of the zero?
I played it in practice mode and it seems to be a legitimate no-zero roulette wheel. There is no system that can either beat or lose to this game in the long run. The more you play the more the ratio of the net win to the total amount bet will get closer to zero.
Update: This casino has since closed.
Two questions for you:
1) Regarding the basic blackjack strategies, you have for different online casino groups. Specifically, two different ones that both use single deck: Microgaming and Unifed Gaming. I cannot understand why you list 11 VS 10 as a hit for Microgaming, but as a double for Unified. Since they both use single deck, it seems the same strategy should be used here. I lose more often than win when I double this.
2) In Roulette, it seems to me that your odds would be better to bet equally on both red, and the 3rd column, or black and the 3rd column. The 3rd column has, I believe, 8 reds and only 4 blacks. Conversely, the first column has more blacks. Does betting like this lower the house edge?
If you double on 11 at a Microgaming casino and the dealer gets a blackjack you will lose the total amount bet. At Unified Gaming the blackjack would be turned over immediately if the up card were a ten so there is no risk of losing to a blackjack when doubling in this situation.
All combinations of bets in roulette yield the same expected return, assuming the dreaded five-number combination is avoided. You're right that the third column has eight reds and four blacks. The probability of winning 3 units is 8/38, 1 unit is 4/38, breaking even is 10/38, and losing 2 units is 16/38. The combined expected per unit bet is return is (1/2)*(3*8 + 1*4 + 0*10 + 2*16)/38 = -2/38. Betting on black and the third column the probability of winning 3 units is 4/38, 1 unit is 8/38, breaking even is 14/38, and losing 2 units is 12/38. The expected return is (1/2)*(3*4 + 1*8 + 0*14 + 2*12)/38 = -2/38. Both combinations weight the various outcomes differently, but they average to the same number.
Hey, Wiz. I am curious to know what the expected number of spins is for an American Roulette wheel before all 38 numbers have been chosen at least once. Is this proportional to the number of selections (38) or is it exponentially related to this number? I tried figuring this out for a 6-sided die but got stuck fast.
Once you have hit n numbers, the probability of getting a new number on the next spin is (38-n)/38. If the probability of an event is p, then the expected number of trials before it happens is 1/p. Thus the expected number of spins to get a new number, given that you already have n, is 38/(38-n). For example once you have hit 20 numbers the expected number of spins to get the 21st is 38/18=2.11. So the answer is the sum of the expected number of spins at each step: (38/38)+(38/37)+(38/36)+...+(38/1)=160.66.
What would be the odds of having a red number turn up 18 times in a row on Roulette.
(18/38)18 =~ 1 in 693745.
I was fascinated to read your comment regarding little steel balls not having a memory. I have a roulette wheel at home and the little balls jump up and down with glee when I come home from hospital. Clearly that’s because they remember me, and what’s more I think they would be offended by your remarks. On my planet roulette is not allowed because the little balls can be bribed so easily. I think your planet stinks and now I can’t afford to repair my spacecraft to get back home.
Oh, and the man behind me in the white coat wants to say that he loves your web site and is grateful for all the work you have put in to show the math. He says it saved him a lot of time and money. Keep up the good work.
I’m happy to have helped the main in the white coat. My roulette advice is limited to games on earth, bribery is recommended on your planet.
I played the same number 1000 spins in a row on a 0,00 wheel and hit 6 times. What are the chances of hitting 6 or fewer times in this scenario?
The probability of your number hitting exactly x times is combin(1000,x)*(1/38)x*(37/38)1000-x. The following table shows the probability of all number of hits from 0 to 6 and the total.
Wins in 1000 Roulette Bets
| Number | Probability |
| 0 | 0.00000000000262 |
| 1 | 0.00000000007078 |
| 2 | 0.00000000095556 |
| 3 | 0.00000000859146 |
| 4 | 0.00000005787627 |
| 5 | 0.00000031159330 |
| 6 | 0.00000139655555 |
| Total | 0.00000177564555 |
So the answer is 0.00000177564555, or 1 in 563175. I hope this didn’t happen at an Internet casino.
You may wonder why I didn’t use the normal approximation as I did with the coin flipping problem above. That is because it doesn’t work well with very high and very low probabilities.
Hi Mike, Just to lighten the mood a little, I remember watching you play roulette on a special Vegas Challenge show a while ago. Obviously you knew your expected value wouldn’t change regardless of strategy. I remember you playing only one number, but I forgot if you changed after a win. Not sure what I’d do in your situation, but out of curiosity, did you play the single number as opposed to an outside bet like red/black to maximize the variance? That way if you get "lucky" you’ll be ahead by the most? Anyway, I enjoyed the fact that you played a really conservative and boring strategy.
You accessed my strategy quite well. I intended to bet the minimum through most of the hour to avoid the house edge grinding me down. The producer was not happy with such a boring strategy so I tried to act more excited than I normally would be. The reason I picked a single number as opposed to an even money bet is that I wanted volatility. I knew if I ended close to my starting point of $10,000 I would probably lose. So I wanted a bigger shot at getting ahead. I stuck with 23 the entire time, although towards the end I added 5 as well. I’m Glad you liked the show.
My question is based more from observations on your part and rumors that I’ve heard on my part. If it’s true that Las Vegas dealers, when they are taught at dealer school, learn how to spin and roll the ball the same way then is it true after observing how a dealer spins, one can determine the quadrant of the wheel the ball might land on?
No. Dealers are taught only the basics and nothing nearly that skillful. In fact if a dealer had that control he could simply get an accomplice to bet wherever he planned for the ball to land and they could easily make millions.
What are the odds of playing 15 spins on European roulette, covering at eight numbers and not getting any of them?
The probability of losing any one spin is 1-(8/37) = 78.38%. So the probability of losing 15 spins is .783815 = 2.59%.
I would like to know how to test an online roulette game, to know the odds and if the odds are honest?
First let me say how not to test any game. You should not record all your play and when you are done look for any kind of anomaly, and then write to me complaining that the casino is cheating. The correct way is to state a hypothesis for how the casino is cheating FIRST, then gather data, and finally see if the data fits your hypothesis. If you don’t know what kind of hypothesis to state I would suggest simply testing for the number of wins and losses, and then bet the same thing every time. If you do the first two steps properly and need help on the third then feel free to write me.
When I enter a casino with $100 and play roulette, I don’t expect to leave it with 4% less but with 25% less. Does this phenomena has a formal name? (I was googling "real house edge") Is there any formula/model to predict this "real house edge"? Which games are better and which are worse in this parameter?
In your example the casino’s hold is 75%. That is the ratio of how the value of chips players walk away with to the amount of money the dealer drops in the box. Although there are historical averages there is no way to go from house edge to hold. The hold depends in part on how long the player will circulate through his chips, and there is no way to know that.
If I have a $200 bankroll that I don’t mind losing, and keep playing $10 on one single number on European (single-zero) roulette, what are the probabilities of winning, $200, $500 or $1000? Assuming I’ll stop after reaching the target. Thanks, great site, you wanted me to keep this short :)
Thanks for the compliment. There is a formula for questions like this, which I explain on my site www.mathproblems.info, see problem 116.
With a bankroll of b units, winning goal of g units, probability of winning p, and probability of losing q your probability of success is ((q/p)b-1)/((q/p)b+g-1). In this case b=20, p=18/37, q=19/37, and g=20, 50, and 100. So for a bankroll of $200 the probability is ((19/18)20-1)/((19/18)40-1) = 0.253252.
For a winning goal of $500 the probability is ((19/18)20-1)/((19/18)70-1) = 0.045293.
For a winning goal of $1,000 the probability is ((19/18)20-1)/((19/18)120-1) = 0.002969.
On a 38 number Roulette wheel....after hitting three reds, a green, and then another red....what are the odds, that the next consecutive three spins would come up red 23?
It doesn’t make any difference what the past spins were. The probability of red 23 three times in a row is (1/38)3 = 1 in 1 in 54,872.
I visited Bodog and tried out their roulette wheel on the free site. In a box in the upper corner it records the last ten numbers that hit. I spun the thing fewer than 20 times, I am sure. The numbers recorded there are as follows: 9-9-29-21-11-11-20-28-32-1 Interestingly, two spins before this there was another hit on 32. Meaning that the numbers 9, 11 & 32 all hit twice within 12 spins. As I said, I am not a statistician, but the frequency of these three numbers coupled with the minimal number of times I spun the wheel seem to indicate something is wrong.
The probability of three pairs and six singletons in twelve spins is combin(38,3) × combin(35,6) × combin(12,2) × combin(10,2) × combin(8,2) × fact(6)/3812 = 9.04%. The math gets rather messy asking about the probability that this could happen in any 12-spin span over 20 total spins. Suffice it to say that it is significantly more than 9%, more likely than not, I would guess. So these seem like very normal results to me.
One of the casinos in my town is paying 36 to 1, for a straight up bet, on a single-zero roulette wheel, on a specified number for that day. For example, the specified number is 8 on the 8th of the month. How does that change the house edge? Thanks for your help.
The house edge on the specified number would be exactly 0%.
The Orleans has a side bet in roulette that pays 8 to 1 on three reds (or blacks) in a row. It is on a double-zero wheel. Can you tell me the odds?
The probability of winning is (18/38)3 = 10.63%. The house edge is 8×0.1063 - 1×0.8937 = 4.34%, which is less than the 5.26% on all the other bets (except the dreaded 0,00,1,2,3 combination at 7.89%).
There are some casinos in Holland allow triple imprisonment in roulette. What is the house edge for even money bets under that rule? I’m more interested in the solution than the answer.
For the benefit of other readers, at many casinos in Europe, if you make an even money bet in roulette and the ball lands in zero, then the wager becomes imprisoned. If the next roll would cause the wager to win, then it is returned without winnings. If the ball lands the opposite way, then the bet loses.
What happens to single-imprisoned bets if the ball lands in zero? If the casino allows only single imprisonment, then it would lose. However, some casinos allow for double imprisonment, which is what would happen. If a double imprisoned bet wins, then it returns to being single imprisoned. If the casino allows only up to double imprisonment, then a double imprisoned bet would lose on another zero. By the same logic, if a casino allows triple imprisonment, then a double imprisoned bet would become triple imprisoned on another zero.
The house edge under triple imprisonment is 1.370120%. Before I explain how I arrived at that, let’s do single and double imprisonment first. Assume the first bet is on red.
Let Z = probability of a zero = 1/37.
Let R = probability of a red number = 18/37.
Single imprisonment
pr(push) = ZR = 0.0131482834.
pr(win) = R = 0.4864864865.
pr(loss) = 1-pr(push)-pr(win) = 0.5003652301.
Expected value = pr(win)-pr(loss) = -0.0138787436.
Double imprisonment
The player will push if the first spin is a zero, then the player can repeat ZR from 0 to an infinite number of times, and then get a red. In other words, the ways to push are:
ZR, Z(ZR)R, Z(ZR)(ZR)R, Z(ZR)(ZR)(ZR)R, ...
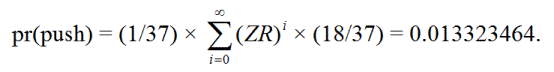
pr(push) = 0.013323464
pr(win) = 18/37 = 0.4864864865.
pr(loss) = 1-pr(push)-pr(win) = 0.5001900494.
Expected value = pr(win)-pr(loss) = -0.0137035629.
Triple imprisonment
First, let’s find the probability p1 that a single imprisoned bet becomes triple imprisoned with two more zeros, and then eventually rises back up to being single imprisoned again. This can happen as follows:
ZZRR, ZZ(RZ)RR, ZZ(RZ)(RZ)RR, ZZ(RZ)(RZ)(RZ)RR, ...
In other words, the bet can bounce between triple and double imprisonment up to an infinite number of times.
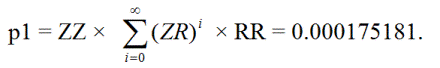
Second, let p2 = the probability that a single imprisoned bet reaches the first or second level of imprisonment and then returns to single imprisonment.
let p2 = ZR + p1 = 0.013323464.
The player can repeat returning to the first level from zero to an infinite number of times. So the probability of a push is:
ZR + Z p2R + Z p2 p2R + Z p2 p2 p2R + ... =
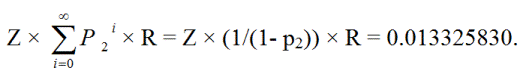
Z × (1/(1- p2)) × R = 0.013325830.
pr(push) = 0.013325830.
pr(win) = 18/37 = 0.4864864865.
pr(loss) = 1-pr(push)-pr(win) = 0.5001876839.
Expected value = pr(win)-pr(loss) = -0.0137011974.
Infinite imprisonment
Not that you asked, Maff, but in Spain I hear they allow infinite imprisonment. Let p = probability of a push. This is also the probability of starting at level x of imprisonment, falling deeper in levels, but eventually climbing back up to x.
p = ZR + ZpR + ZppR + ZpppR + ...

p2 - p + ZR = 0
By the Quadratic Formula p = (1-(1-4*RZ)1/2)/2 = 0.0133258620.
pr(push) = 0.0133258620.
pr(win) = 18/37 = 0.4864864865.
pr(loss) = 1-pr(push)-pr(win) = 0.5001876515.
Expected value = pr(win)-pr(loss) = -0.0137011650.
Zeros ignored imprisonment
Finally, at some casinos zeros are simply ignored after the first zero which imprisons the bet. There the probability of a push is simply (1/37)×(1/2) = 0.0135135135.
The following table summarizes all four kinds of rules.
Imprisonment Odds
| Imprisonment | Win | Push | Loss | Expected Value |
| Single | 0.48648649 | 0.01314828 | 0.50036523 | -0.01387874 |
| Double | 0.48648649 | 0.01332346 | 0.50019005 | -0.01370356 |
| Triple | 0.48648649 | 0.01332583 | 0.50018768 | -0.01370120 |
| Infinite | 0.48648649 | 0.01332586 | 0.50018765 | -0.01370117 |
| Zeros ignored | 0.48648649 | 0.01351351 | 0.50000000 | -0.01351351 |
I’d like to thank ChesterDog and weaselman for their mathematical help. I’d also like to give thanks and a plug to professor G. Artico and polarprof.it for the HTML of the summation formula above.
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
Is there any pattern to the order of the numbers on the roulette wheel?


The idea is that the wheel should be balanced. In other words, if you took the average of a section of consecutive numbers on the wheel, they would be close to the average number 18.5. I thought of a way to explain how the numbers are distributed on a double-zero wheel, as follows.
- Position the 00 at the 12:00 position and the 0 at the 6:00 position.
- The numbers at the top of the wheel are 13, 1, 00, 27, 10*, 25. This must simply be memorized.
- All low odd numbers (from 1 to 17) are on the left side and the high odds (19 to 35) on the right side.
- Starting with the 1 and 13, move four positions counter-clockwise to get the next odd, but do not pass the zero.
- As an exception to rule 4, do not place the 19 four positions counter-clockwise from the 17, because the 19 is a high odd and belongs on the right side. Instead, put the 11, the only low odd not otherwise covered in rule 4.
- All even numbers are directly across the wheel, 180 degrees, from the preceding odd number.
I'm at a loss to explain the order on a single-zero wheel. For now, I can say that if you put the zero in the 12:00 position, then:
- On the left side will be all red low numbers and black high numbers.
- On the right side will be all red high numbers and black low numbers.
This question is raised and discussed in my forum at Wizard of Vegas.
I tracked 3,000 spins in double-zero roulette because the first dozen numbers did not seem to come up as much the second two dozens. In the 3,000 spins, the numbers in the range of 1 to 12 came up 742 times. What are the odds of that?
You would expect the number of times the ball would land in 1 to 12 to be 3000*(12/38) = 947.37.
The difference between your results and expectations is 947.37 - 742 = 205.37.
The variance is 3000*(12/38)*(1-(12/38)) = 648.20.
The standard deviation is the square root of the variance = sqrt(648.20) = 25.46.
Your results are 205.37/25.46 = 11.75 standard deviations south of expectations.
The p value, or the probability of being off by 11.75 standard deviations or more is 1 in 28,542,806,257,940,300,000,000,000,000,000.
I would be interested to know where the wheel is.
What is your opinion of the Comp Killer roulette strategy, as covered in this video?
It's easy to see the purpose of that system is to cover most numbers so it's a fairly low risk way of playing roulette. Here is what to bet on each spin:
- $5 each on 3, 16, 24, 28, and 33.
- Make a corner bet on each of these sets of numbers: 2/3/5/6, 7/8/10/11, 14/15/17/18, 19/20/22/23, 26/27/29/30, 31/32/34/35.
Note that this does not cover the following nine numbers: 0, 00, 4, 9, 12, 13, 21, 25, and 36.
The following return table shows the probability and contribution to the return of all possible outcomes.
Comp Killer
| Event | Net Win | Combinations | Probability | Return |
|---|---|---|---|---|
| Straight up win | 5 | 5 | 0.131579 | 0.657895 |
| Corner win | 50 | 24 | 0.631579 | 31.578947 |
| All other | -175 | 9 | 0.236842 | -41.447368 |
| Total | 38 | 1.000000 | -9.210526 |
The lower right cell shows an expected loss of $9.21 per spin. The total amount bet per spin is $175. This results in a house edge of $9.21/$175 = 5.26%, the house edge in double-zero roulette.
I would like to add that you will probably lose more than you get back in comps with this strategy, or any roulette strategy. The rule of thumb is casinos will give you back about 1/3 of your expected loss in comps. There are ways of fooling the casinos that your expected loss is more than it really is, but playing this strategy isn't one of them.
What do you think of this strategy in roulette:
- Bet two units on black
- Bet one unit on the third column
The beauty of this strategy is there are 8 red numbers and 4 black numbers in the third column. Of the 16 red numbers, half are on columns 1 or 2 and half are on column 3. Let’s ignore the 0 and 00 for now. When the ball lands in red, 8 out of the 18 red numbers are in the third column. If the probability of winning is 8/18 and wins pay 2 to 1, I have a player advantage of 33.3%. Even if we average that with the bet on black with 0% house edge, again ignoring 0 and 00 for now, I still have a 16.7% player advantage. Mixing in the 0 and 00, isn’t my advantage (2/38)*-100% + (36/38)*16.7% = 10.53%! What do you think?
I agree that the conditional advantage of the third column bet is 33.3%, assuming the ball lands in red, and ignoring both zeroes. However, by the same logic, if the ball lands in black, the probability of the third column bet winning is 4/18 = 2/9. A bet with a 2/9 chance of winning that pays 2 to 1 would have a house advantage of 33.33%. So, looking at it your way, the third column bet would have a player advantage of 33.33% half the time and a house edge of 33.33% the other half. Cancelling each other out, that bet has 0% house edge. Finally, mix in the two zeros and the overall player edge is (2/38)*-100% + (36/38)*0% = -5.26%.
Looking at it another way, the following table shows the number of ways all possible outcomes can occur, the probability, units won, and the contribution to the return. The lower right cell shows an an expected loss of -0.105263 units. Divided by the two units bet, that comes to a house edge of 5.26%.
Bohemia Strategy
| Event | Pays | Numbers | Probability | Return |
|---|---|---|---|---|
| 0, 00 | -2 | 2 | 0.052632 | -0.105263 |
| Red & column 1 or 2 | -2 | 10 | 0.263158 | -0.526316 |
| Red & column 3 | 1 | 8 | 0.210526 | 0.210526 |
| Black & column 1 or 2 | 0 | 14 | 0.368421 | 0.000000 |
| Black & column 3 | 3 | 4 | 0.105263 | 0.315789 |
| Total | 38 | 1.000000 | -0.105263 |
What is the expected number of spins required to get five reds or five blacks in a row?
Here is my solution (PDF).
This question is asked and discussed in my forum at Wizard of Vegas.
I hear quadruple-zero roulette is now out there. What is the house advantage?

Yes, such a wheel is marketed by TCS John Huxley. I am not aware of any placements yet.
The formula for the house edge in standard roulette is z/(36+z), where z = number of zeroes. In this case, the house edge is 4/(36+4) = 4/40 = 1/10 = 10%.




