Ask The Wizard #410
I see you answered a question about the Plinko game on the Price is Right in Ask the Wizard column #115. However, they sometimes change the prize amounts for special shows. For example, on Big Money Week, the prizes from left to right were $500, $1000, $2500, $0, $200000, $0, $2500, $1000, $500. What would be the expected value for each position the puck is dropped from? What is the probability the puck lands in any given prize given any given starting position?
There are nine starting positions to drop the puck from. However, we need to concern ourselves with only five because the prizes and peg layout are symmetric. Let's label them, starting from the left edge, 1 to 5.
There are also nine ending positions, let's label the first five, starting from the left, 1 to 5 as well.

The following table shows the probability of landing in any given spot (left column) according to the position dropped from (top row).
| Landing Spot | Drop 1 or 9 | Drop 2 or 8 | Drop 3 or 7 | Drop 4 or 6 | Drop 5 |
|---|---|---|---|---|---|
| 1 or 9 | 0.225586 | 0.193359 | 0.121094 | 0.056641 | 0.032227 |
| 2 or 8 | 0.386719 | 0.346680 | 0.250000 | 0.153320 | 0.113281 |
| 3 or 7 | 0.242188 | 0.250000 | 0.257813 | 0.250000 | 0.242188 |
| 4 or 6 | 0.113281 | 0.153320 | 0.250000 | 0.346680 | 0.386719 |
| 5 | 0.032227 | 0.056641 | 0.121094 | 0.193359 | 0.225586 |
| Total | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
The next table shows the expected value from each dropping position for the Big Money Week you asked about. As expected, the player should drop the puck direction over the largest prize.
| Drop Location | Expected Win |
|---|---|
| 1 or 9 | $7,550.29 |
| 2 or 8 | $12,396.48 |
| 3 or 7 | $25,173.83 |
| 4 or 6 | $39,478.52 |
| 5 | $45,852.05 |
What is the Gabriel's Horn paradox?
First consider the curve from by the equation y=1/x for values of x from 1 to infinity. That graph will look as follows for values up x up to 17.
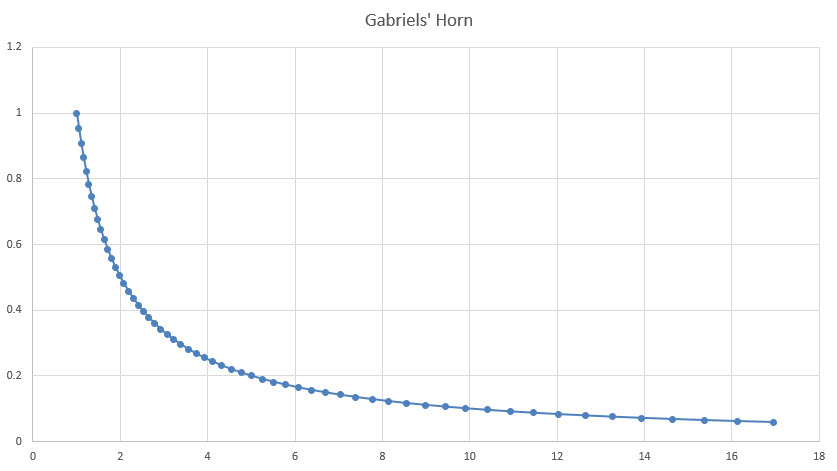
Next, imagine that curve being rotated around the x axis. It will create what looks like a horn, with an infinitely long end. That is what mathematicians call Gabriel's Horn?

Image source: Soul of Mathematics.
Next, consider the questions about Gabriel's Horn:
- What is the volume?
- What is the surface area?
Here are the answers:
- Volume = π = pi.
- Surface area = infinity
My work showing these answers can be found here (PDF).
The nature of the paradox asks how can the volume be finite yet the surface area infinite?
The perceived paradox occurs when we confuse two dimensions with three. We just shouldn't do that. Consider circle A with radius 1 and circle B with radius 1.1, where circle A is inside circle B.
Circle A has a circumference of 2*pi =~= 6.283185 and circle B has an area of of 1.1^2 * pi =~ 3.801327. Note that circle B is larger than circle A, yet it's area is less than the circumference of B. It is not that the circumference of B is part of the area of A. The area and circumference are different measurements in different dimensions and shouldn't be compared.
Another way to look at it is if we made a record out of circle A with an infinite number of grooves, the length of those grooves would be infinity.
Getting back to Gabriel's Horn, consider simplifying it to the discreet case of circles with radius 1, 1/2, 1/3, 1/4 ...
The sum of the volumes of these circles would be pi*(1/1 + 1/4 + 1/9 + 1/16 + ...). There is a well-known infinite series that say:
1/1 + 1/4 + 1/9 + 1/16 + ... = pi^2/6 =~ 1.644934.
Adding another pi term, the sum of the areas of the circles is pi^3/6 =~ 5.167713.
Meanwhile, the sum of the circumferences is 2*pi(1/1 + 1/2 + 1/3 + 1/4 + ...).
It is another well known infinite series in mathematics called the Harmonic Series that says:
1/1 + 1/2 + 1/3 + 1/4 + ... = ∞ = infinity.
2*pi*∞ still equals ∞.
If we extend this logic to infinitely small distances between circles, we get Gabriel's Horn.
Nathan buys 100 pounds of beans. The beans consist of 99% water by weight. She leaves them in the sun to let them dry out. The next day, she finds they consist of 98% water. What is their new weight?
Let:
- w = Original water weight.
- w' = Water weight after drying out the beans.
- x = Weight of everthing else in the beans.
We are given for the first day:
w + x = 100
w/(w+x) = 0.99
Substituting the first equation into the second:
w/100 = 0.99
w = 99
Thus, x=1.
The next day, we are given:
w'/(w'+x) = 0.98
w' = 0.98*(w'+x)
0.02w' = 0.98x
We know x=1 so:
0.02w' = 0.98
w' = 0.98/0.02 = 49
The total weight the next day is x+w' = 1+49 = 50.


