Ask The Wizard #392
Which Las Vegas casinos still have buffets?
Good question. Many properties got rid of them during the pandemic closure. Here is a list of those that survived. Please be advised many have limited days and hours of operation.
- Bellagio
- Caesars Palace
- Circus Circus
- Cosmopolitan
- Excalibur
- Main Street Station
- MGM Grand
- Palms
- Rampart
- South Point
- Westgate
- Wynn
This question is asked and discussed in my forum at Wizard of Vegas.
Consider an 8/5 Bonus Poker progressive with a 0.5% meter rise. Player A must have a player advantage immediately to play. Player B is patient and will play until the jackpot hits, but still requires a long-term advantage. What is the minimum jackpot for each player to play? You may assume a stand-alone machine that is not part of a linked progressive.
The return from the fixed pays in 8/5 Bonus Poker is 0.971776. Let's assume the player uses strategy for a royal that pays 800. The probability of a royal is thus 0.0000248551. Let j be the breakeven jackpot to have an immediate 100% return on the game. Then:
1 = 0.971776 + j × 0.0000248551
j = (1-0.971776)/0.0000248551 = 1135.56.
So, player A would need at jackpot of at least 1136 full 5-credit bets (rounding up) to play. Player A does not need to care about the meter rise.
Player B is in it for the long term. He will eventually get back whatever the 0.5% meter rise. His calculation is similar, except he values that meter rise. His breakeven value of j can be defined as:
1 = 0.971776 + 0.005 + j × 0.0000248551
j = (1-0.971776-0.005)/0.0000248551 = 934.39.
Rounding up, player B would need a jackpot of 935 full 5-credit bets.
This question is asked and discussed in my forum at Wizard of Vegas.
What is the formula for 13 + 23 + 33 + 43 + ... + n3?
Here is a link to my solution (PDF).
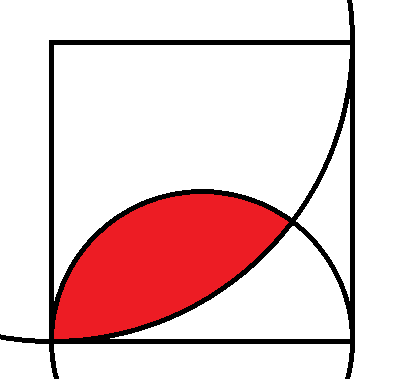
The square above has side length 2. One arc is of a circle of radius 1 and the other radius 2. What is the area of the red region? It is allowed to express your answer in trig functions.
Here is my solution (PDF).
Source of this question: Presh Talwalkar of the YouTube channel Mind Your Decisions.




