Ask The Wizard #383
It takes Alice and Bill 3 hours to paint a house.
It takes Alice and Cindy 4 hours to paint a house.
It takes Bill and Cindy 5 hours to paint a house.
How long does it take if they all paint?
A rubber band is stretched over two adjacent circles of diameters 2 and 5. What is the length of the stretched rubber band?
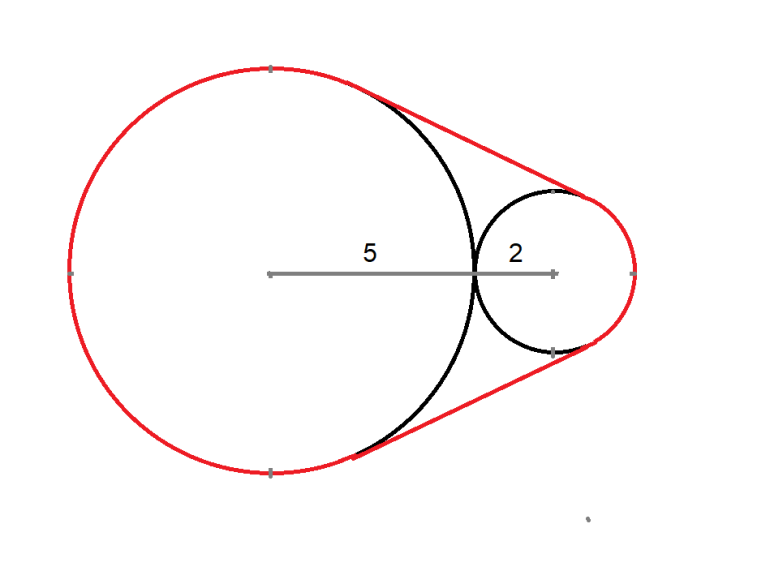
Here is my solution (PDF).
This problem is asked and discussed in my forum at Wizard of Vegas.
Consider a game of rock-paper-scissors where:
- If rock beats scissors, scissors pays rock $1
- If scissors beats paper, paper pays scissors $2
- If paper beats rock, rock pays paper $3
- No money changes hands on a tie
Assume two logicians are playing. What is the optimal strategy for each?
- Play paper with probability 1/6
- Play rock with probability 1/3
- Play scissors with probability 1/2
Let's define some probabilities for the logician seeking to maximize his winnings:
- r = Probability of playing rock
- p = Probability of playing paper
- s = Probability of playing scissors
It's clear that r+p+s = 1. Given r and p, s = 1-r-p.
If two logician's play, then both would be indifferent to what their opponent plays, assuming they randomize their choice.
The expected win of the opponent play rock is: 3p-(1-r-p) = 4p+r-1
The expected win of the opponent play paper is: 2(1-r-p) - 3r = 2-5r-2p
The expected win of the opponent play scissors is: r - 2p
These three equations should all be equal.
Setting the first and third equal to each other we get:
4p+r-1 = r - 2p
p = 1/6
Setting the first and second equal to each other we get:
2 -5r - 2p = 4p + r -1
We already know p=1/6, which easily leads us to r=1/3.
s=1-r-p = 1-(1/3)-(1/6) = 1/2.
So, both should play paper with probability 1/6, rock with 1/3, and scissors with 1/2.
The general case for this puzzle is to play each option according to the weight of how much money changes hands if the OTHER two symbols were played.
This problem is asked and discussed in my forum at Wizard of Vegas.




