Ask The Wizard #373
I am sure you're a fan of the Big Bang Theory. One of my favorite scenes is the game of Rock Paper Scissors Lizard Spock. It is like a five-symbol game of Rock Paper Scissors, with the following rules:
- Paper covers rock
- Rock crushes lizard
- Lizard poisons Spock
- Spock smashes scissors
- Scissors cuts paper
- Lizard eats paper Spock vaporizes rock
- Scissors decapitates lizard
- Paper disproves Spock
- Rock crushes scissors
My question is can more symbols be added, such that every side has the same chances against a random player?
Yes, I love that scene too! Here is a YouTube video of it.
You need an odd number of symbols. In theory, you could have an even number, but then you would have to make rules where certain pairs of different symbols resulted in a tie. No, we want a decisive game where the only ties are if both players play the same symbol.
A solution is especially elegant and easy to explain with a prime number of symbols. Allow me to explain with seven symbols, as an example. Let's label the symbols A to G and represent them on a circle, in the following diagram.
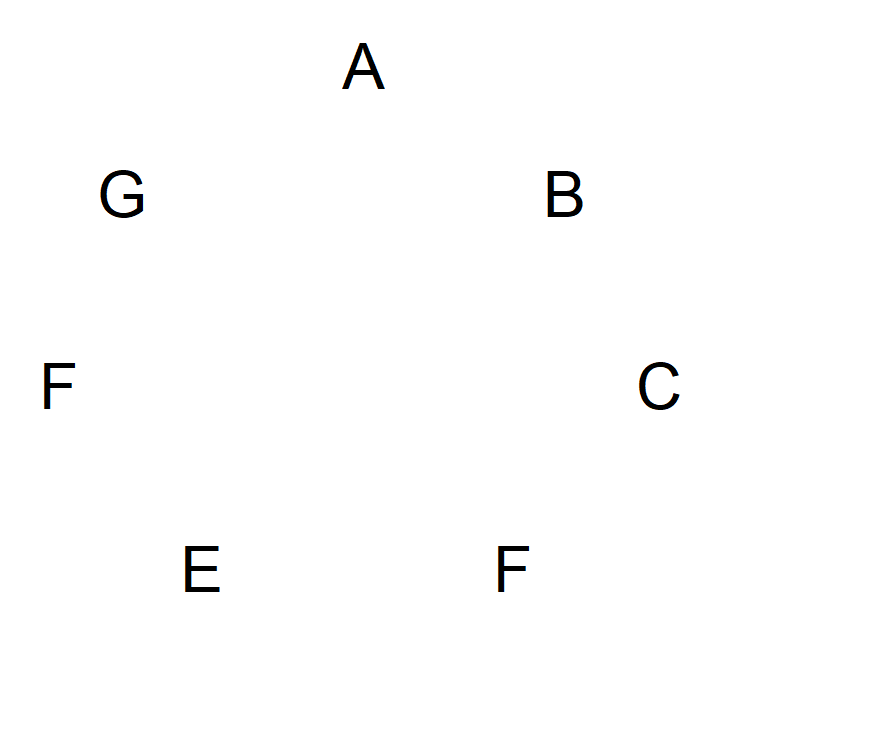
Next, start with A and then draw an arrow to the next symbol going clockwise. The arrow shall point towards that loses between these two. Think of it like that symbol being shot with an arrow. Keep going clockwise until you get back to A. The diagram will not look like this:
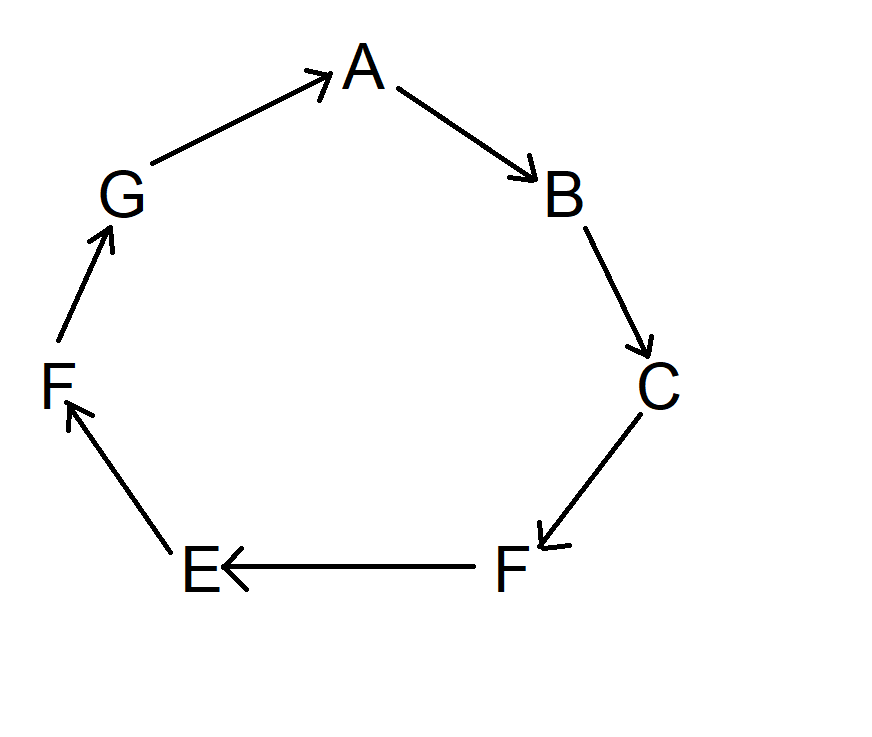
Next, do the same thing, but go two symbols clockwise, starting at A. Actually, you can start anywhere you wish. The diagram now looks like this:
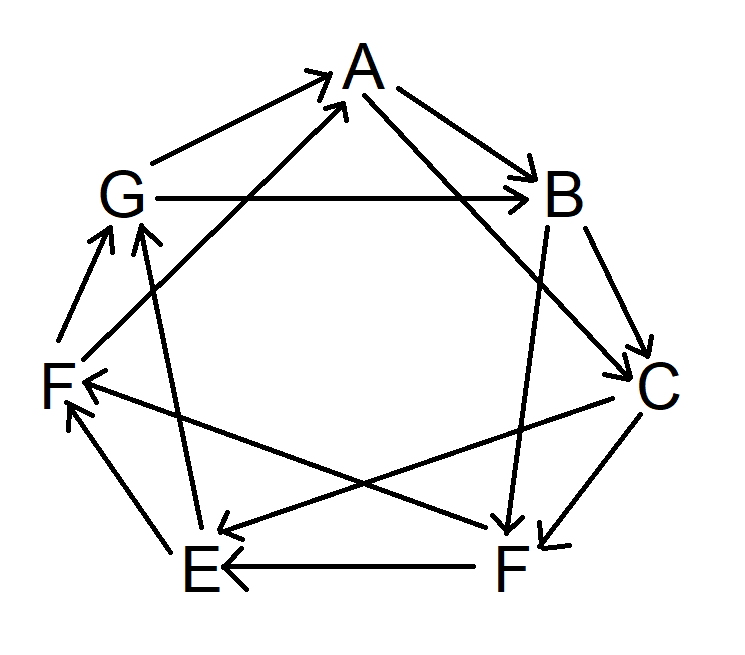
Finally, do the same thing, but skip three symbols clockwise. The diagram now looks like this:
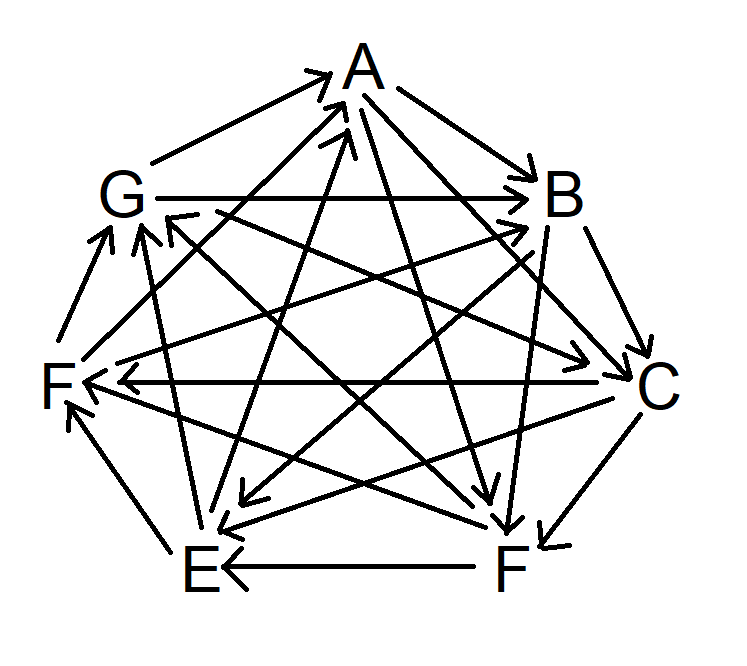
Note at this point every symbol beats three other symbols and is beaten by three other different symbols.
This method will work for any prime number of symbols because by the time you circle back to the original symbol you will have passed through every symbol. For n symbols, you'll have to go through this process (n-1)/2 times.
You can make a balanced game with any odd number of symbols, but you'll loop back to the original symbol too quickly sometimes. When that happens, you'll have to make other loops starting at the symbols you missed.
This question is asked and discussed in my forum at Wizard of Vegas.
What is the probability of a tie in Three Card Poker?
The exact answer is 450528/407170400 =~ 0.001106485 =~ 1/904.
The following table shows the number of ways to make each type of initial hand and the number of combinations that tie in the second hand. With straights and trash hands it matters whether there are two or three suits represented in the first hand.
The bottom right cell shows there are 450,528 ways to tie in Three Card Poker. The total number of combinations for two hands is combin(52,3)*combin(49,3) = 407170400. Thus, the answer is 450528/407170400.
Three Card Poker Tie
| Hand | Hand 1 | Hand 2 | Product |
|---|---|---|---|
| Three of a kind | 52 | 0 | 0 |
| Straight flush | 48 | 3 | 144 |
| Straight (three suits) | 288 | 26 | 7,488 |
| Straight (two suits) | 432 | 25 | 10,800 |
| Flush | 1,096 | 3 | 3,288 |
| Pair | 3,744 | 3 | 11,232 |
| Junk (three suits) | 6,576 | 26 | 170,976 |
| Junk (two suits) | 9,864 | 25 | 246,600 |
| Total | 22,100 | 450,528 |
What is the value of a free ace coupon in 6-5 blackjack?
In my value of a free ace page I state it's value is 50.1844% of the bet amount in 3-2 blackjack.
In six-deck blackjack, the probability of getting a winning blackjack, given an ace as the first card, is 29.3139%. When that happens, you win 0.3 less units in 6-5 blackjack than 3-2.
So the value of a free ace in 6-5 six-deck blackjack is 50.1844% × 29.3139 × 0.3 = 41.3902% of the initial bet.
Somebody challenged me to a bet that he could roll a total of 12 with two dice within 27 rolls. If he didn't, I would win even money. Since the probability of rolling a 12 is 1/36, shouldn't it take him 36 rolls on average to roll a 12? It would seem the odds were in my favor if my opponent got only 27 rolls. Am I right or where is the flaw in my math?
The average waiting time between 12's is indeed 36 rolls, including the 12 roll itself. However, that doesn't mean they come along exactly every 36 rolls. The probability of NOT rolling a 12 is (35/36). The probability of not doing so over 27 rolls is (35/36)^27. So, the probability of at least on 12 is 1-(35/36)^27 = 53.26%.
The following table shows the probability of rolling at least on 12 for 20 to 36 rolls. Note that 25 are needed to have an advantage at even money.
Probability 12
| Rolls | Probability |
|---|---|
| 20 | 43.07% |
| 21 | 44.66% |
| 22 | 46.19% |
| 23 | 47.69% |
| 24 | 49.14% |
| 25 | 50.55% |
| 26 | 51.93% |
| 27 | 53.26% |
| 28 | 54.56% |
| 29 | 55.82% |
| 30 | 57.05% |
| 31 | 58.24% |
| 32 | 59.40% |
| 33 | 60.53% |
| 34 | 61.63% |
| 35 | 62.69% |
| 36 | 63.73% |




