Ask The Wizard #371
I see that Alaska now does elections for Congress by the ranked choice. Assuming 22 candidates, which was the case in the 2022 election for the single House seat, and 200,000 votes, what is the least number of first-choice votes the ultimate winner can have?
For those unfamiliar with how ranked choice elections work:
- Voters are asked to rank their choices from first to last.
- If any candidate gets a majority of the votes, then he* wins.
- Otherwise, the candidate who came in last is eliminated. On all votes, all candidates who are behind that losing candidate in order of preference move up one notch.
- Votes are recounted.
- Go back to step 2, until somebody gets a majority.
*: Forgive for using “he.” I truly mean “he or she,” but hate to write it that way every time I must use pronouns. I also consider the use of “they” to be incorrect grammar, as “they” is supposed to be a plural pronoun.
For example, consider a place with 11 voters and four candidates. The eleven voters rank their candidates as follows:
| Choice 1 | Choice 2 | Choice 3 | Choice 4 |
| B | A | C | D |
| C | B | A | D |
| C | A | D | B |
| D | A | C | B |
| A | D | B | C |
| B | A | D | C |
| B | D | A | C |
| B | D | C | A |
| C | D | B | A |
| A | D | B | C |
| A | B | D | C |
Following is a count of the first place votes in the first round of voting:
| Candidate | Rank 1 Votes |
| A | 3 |
| B | 4 |
| C | 3 |
| D | 1 |
Nobody won a majority of the first place votes, so the losing candidate D is eliminated. He is basically wiped off the votes, with every candidate behind him in rank order shifting up one spot, as follows:
| Choice 1 | Choice 2 | Choice 3 |
| B | A | C |
| C | B | A |
| C | A | B |
| A | C | B |
| A | B | C |
| B | A | C |
| B | A | C |
| B | C | A |
| C | B | A |
| A | B | C |
| A | B | C |
Following is a count of the first place votes in the second round of voting:
| Candidate | Rank 1 Votes |
| A | 4 |
| B | 4 |
| C | 3 |
Nobody won a majority of the first place votes in the second round, so the losing candidate C is eliminated. After he is elimated, the third round votes look like this:
| Choice 1 | Choice 2 |
| B | A |
| B | A |
| A | B |
| A | B |
| A | B |
| B | A |
| B | A |
| B | A |
| B | A |
| A | B |
| A | B |
Following is a count of the first place votes in the second round of voting:
| Candidate | Rank 1 Votes |
| A | 5 |
| B | 6 |
B, thus wins the election with six votes in the third round of voting.
To answer your question with 22 candidates and 200,000 votes, a candidate can win with two votes only as first place. There are a number of ways this could happen. For example, the following first place vote totals:
| Candidate | Total First Place |
| A | 85,311 |
| B | 57,344 |
| C | 28,672 |
| D | 14,336 |
| E | 7,168 |
| F | 3,584 |
| G | 1,792 |
| H | 896 |
| I | 448 |
| J | 224 |
| K | 112 |
| L | 56 |
| M | 28 |
| N | 14 |
| O | 7 |
| P | 2 |
| Q | 1 |
| R | 1 |
| S | 1 |
| T | 1 |
| U | 1 |
| V | 1 |
| Total | 200,000 |
If everybody other than the two P first votes put candidate P as their second choice, then candidate P would win.
In fact, P wouldn't need to be in second place all the time. P could be in second place for only the six votes that put Q, R, S, T, U, and V first. After that, it wouldn't hurt P if previous eliminated candidates were ahead of him in ranked choice.
Consider a semicircle, of radius 1, with two stacked rectangles inside. What is the maximum combined area of the two rectangles?
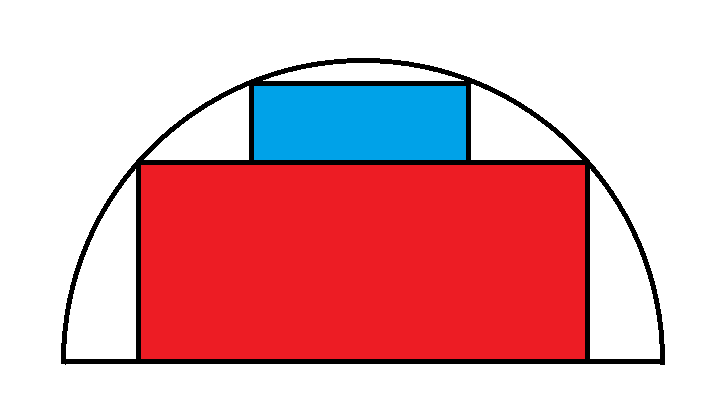
Here is my full solution (PDF).
This question is asked and discussed in my forum at Wizard of Vegas.
Do unicorns have wings?
No.
A horned horse with wings is known as a cerapter, pegacorn, alicorn, or unisus. Not that you asked, but a horse with wings put no horn (I know of only one such case) is Pegasus. Unicorns have a horn, but no wings.
Please ignore identical twins and assume every child has a 50/50 chance of being a born a boy or girl. If children are randomly polled from family sizes of a specified size of 2 to 5, what is the probability a boy or girl will have a sister?
Interestingly, the probability is the same for either gender, regardless of family size.
Let's look at family sizes of three, for example. Here are the eight possible ways to arrange boys and girls, with regard to order:
BBB
BBG
BGB
BGG
GBB
GBG
GGB
GGG
If you pick any girl at random from the list above, you'll see that of the 12 girls, 9 have sisters. It is the same for the 12 boys, 9 have sisters. So, the probability is 9/12 = 3/4.
The general formula for the probability of any child having a sister, where the number of children is n, is 1-(1/2)n-1.
Here is the probability of having a sister by total number of children in the family:
- 1: 0
- 2: 1/2
- 3: 3/4
- 4: 7/8
- 5: 15/16
- 6: 31/32
Alternatively, it makes sense the probability would be the same for boys and girls. The gender of your siblings is not correlated to your gender. Thus, only family size matters, not your own gender.
This question is asked and discussed in my forum at Wizard of Vegas.




