Ask The Wizard #370
Your advice to seek value in playing the lottery is terrible! You clearly don’t understand that lottery players don’t care about the odds or value, but just want a chance, any chance, at a big jackpot and don’t really care about the smaller prizes.
My advice for all forms of gambling is based on maximizing how much the player can expect to get back from his bet. In my 25 years of analyzing gambling, that policy has done well for me and you’re the first one to attack me for it.
However, I’m always open to considering other points of view. In this effort, let’s consider a player who cares equally about excitement and value. This player is not going to be happy with low-volatility games, but rather wants to win the whole chandelier or lose trying. To quantify any given bet for such a player, I have created a statistic I call the Excitement Quotient. This I define as the ratio of the standard deviation to element of risk. As a reminder, the element of risk is the ratio of expected player loss to the average amount bet by the end of the hand (including subsequent wagers like doubling in blackjack and raising in poker variants).
The following table shows the Excitement Quotient for a variety of casino games and bets, in order from highest to lowest. It does indeed show that for such an excitement-seeking player, the Mega Millions offers the most excitement for the money.
Excitement Quotient
| Game | Bet | Standard Deviation |
Element of Risk |
Excitement Quotient |
|---|---|---|---|---|
| Mega Millions | 40M jackpot, no Megaplier* | 1158.38 | 0.8104 | 1429.38 |
| Video poker | 25-15-9 Deuces Wild | 5.06 | 0.0109 | 465.68 |
| Video keno | Pick-8 spot keno: 2,12,98,1652,10000 pay table | 29.96 | 0.0769 | 389.56 |
| Blackjack | Liberal low-limit rules** | 1.15 | 0.0049 | 236.60 |
| Roulette | Double zero game, single number bet | 5.76 | 0.0526 | 109.49 |
| Baccarat | Banker bet | 0.93 | 0.0106 | 87.74 |
| Craps | Pass line | 1.00 | 0.0141 | 70.71 |
| Pai gow poker | Dealer banker, house way | 0.75 | 0.0272 | 27.57 |
| Roulette | Double zero game, even money bet | 1.00 | 0.0526 | 18.97 |
*: The line for the Mega Millions does not consider the annuity or taxes.
**: Blackjack assumes six decks, blackjack pays 3-2, dealer hits soft 17, double after split allowed, surrender allowed, re-splitting aces allowed.
Thank you for the comment and for the insult.
This question is asked and discussed in my forum at Wizard of Vegas.
Three points are distributed randomly and uniformly along a circle with radius 1. What is the expected minimum distance between the three points, where distances are measured along the circumference?
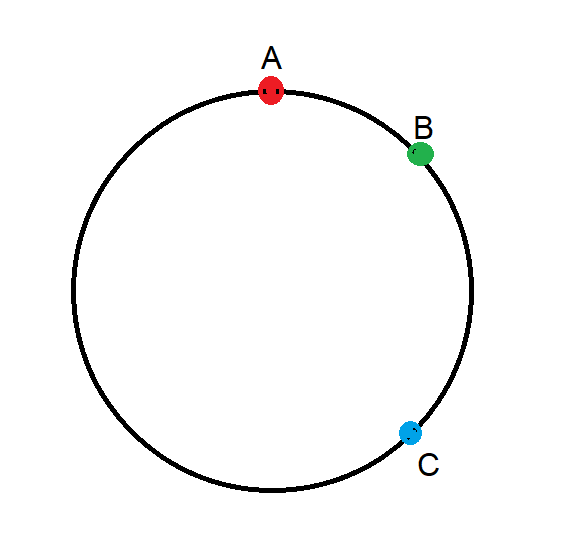
Here is my solution (PDF).
This question is asked and discussed in my forum at Wizard of Vegas.
The cross section of a shed is a 10 foot by 10 foot square. The shed is located in the center of an open, level field.
A goat is tethered to one corner of the shed by a forty foot rope. The goat cannot enter the shed.
What is the area over which the goat can graze?
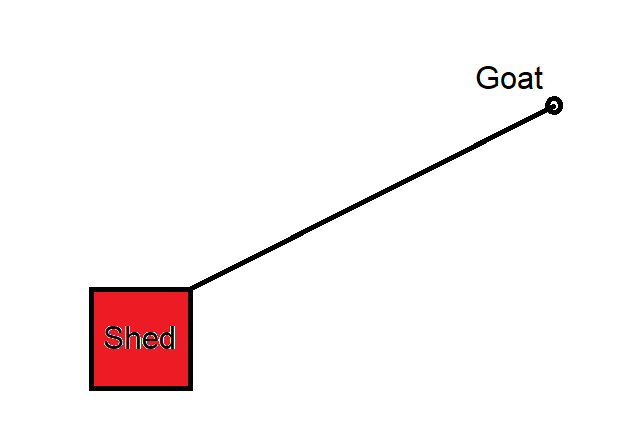
Consider the following diagram, for purposes of discussion.
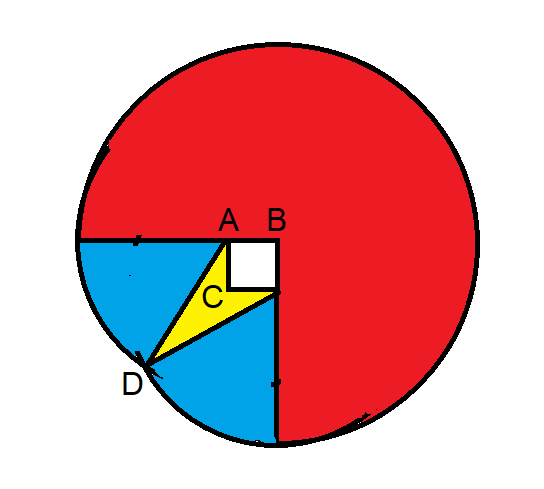
The area the goat can graze is the sum of the red, blue, and yellow regions.
It is important to solve for the angle ADC, which is atan(sqrt(2)/sqrt(34)) =~ 0.237941125 radians.
Forgive me if I don't get into the details, but here are the areas of each region, by color:
- Red = 3769.911184
- Blue = 921.005359
- Yellow = 156.155281
- Total = 4847.071825
This question is asked and discussed in my forum at Wizard of Vegas.




