Ask The Wizard #367
I like to bet all the numbers in craps. How many unique numbers can I expect to hit before a 7-out?
For the benefit of other readers, the question is asking how many of the following totals will be rolled two dice before a total of seven is rolled: 4, 5, 6, 8, 9, and 10.
The answer is 2.375758. The following table shows the probability of each individual possibility of rolling zero to six unique totals in the range specified. The lower right cell shows the average unique totals rolled before a seven.
Unique Numbers Rolled
| Total | Probability | Expected |
|---|---|---|
| 6 | 0.062168 | 0.373009 |
| 5 | 0.101016 | 0.505079 |
| 4 | 0.129245 | 0.516979 |
| 3 | 0.151531 | 0.454594 |
| 2 | 0.170057 | 0.340114 |
| 1 | 0.185983 | 0.185983 |
| 0 | 0.200000 | 0.000000 |
| Total | 1.000000 | 2.375758 |
Is it true the flip of a fair coin is more likely to land face-up on the side that started face up?
The evidence suggests this is true!
Persi Diaconis and Susan Holmes of Stanford University recorded 10,000 coin flips. The coin landed on the same side face-up as it started 50.8% of the time (source: The Fifty-one Percent Solution from the newsletter What’s Happening in the Mathematical Sciences by the American Mathematical Society). The probability of a ratio that high or more is 5.48%.
To prove this mathematically, I assumed the actual number of revolutions of a coin followed the Poisson distribution. To be more specific, if the mean number of revolutions was m, then the probability of exactly n revolutions is exp(-m)*m^n/n!. To illustrate the Poisson distribution, the following graph shows the probability of 0 to 25 revolutions, given a mean of 10.
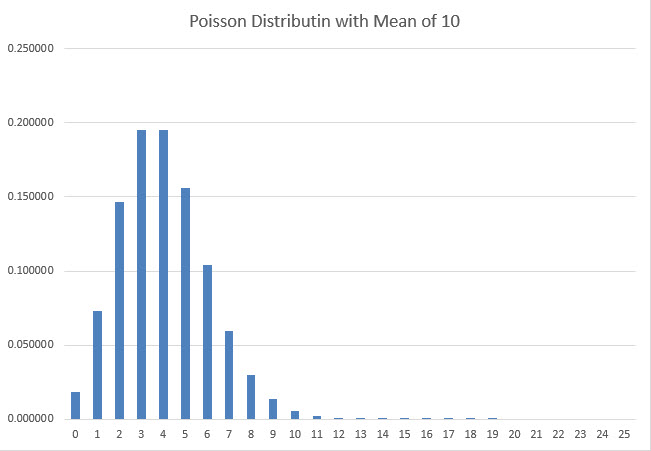
The reasons I chose the Poisson assumption is it follows a near bell curve shape for sufficiently large means and the actual result can never go below zero.
I then calculated the probability of an even number of half-revolutions (resulting in the same side landing face up as the starting position) for various means of half revolutions. The following table shows the results for 0.5 to 5.0 means.
Probability Even and Odd Number of Revolutions
| Mean Revolutions | Even Total | Odd Total |
|---|---|---|
| 0.5 | 0.567667642 | 0.432332358 |
| 1 | 0.509157819 | 0.490842181 |
| 1.5 | 0.501239376 | 0.498760624 |
| 2 | 0.500167731 | 0.499832269 |
| 2.5 | 0.500022700 | 0.499977300 |
| 3 | 0.500003072 | 0.499996928 |
| 3.5 | 0.500000416 | 0.499999584 |
| 4 | 0.500000056 | 0.499999944 |
| 4.5 | 0.500000008 | 0.499999992 |
| 5 | 0.500000001 | 0.499999999 |
I then got to wondering why the probability of an even number was always greater than 50%. It turns out the probability of an even number, given a mean of m, can be expressed as 0.5 + e^(-2m)/2. e to the power of anything must be positive, thus the probability of an even number of revolutions is also positive.
You can see my proof of this formula here.
What is your analysis of the Spelling Bee game on the Price is Right?
For the benefit of other readers, let me go over the rules first.
- There is a board with 30 cards, numbered 1 to 30.
- On the back side of each card is a letter or the word "car." The distribution of each is as follows:
- C: 11
- A: 11
- R: 6
- Car: 2
- The hosts let's the player choose two cards.
- After a pricing game, which I won't get into, the player has the opportunity to earn up to three more cards.
- The cards will be flipped over.
- The player can win a car one of two ways:
- The player gets at least one card of each letter (thus spelling the word CAR).
- The player gets at least one of the "CAR" cards.
- At any point in the game, the player may surrender and receive $1,000 for each of his cards left unturned.
Here is a clip of the game being played.
The following table shows the probability of winning, according to how many cards the player has, assuming none have been turned over yet.
Spelling Bee — Probability of Winning
| Cards | Probability Winning |
|---|---|
| 2 | 0.131034 |
| 3 | 0.371921 |
| 4 | 0.584018 |
| 5 | 0.734888 |
Before any cards are turned, the player should not surrender, assuming any reasonable value of the car. For example, even with only two cards, the player has a 13.1% chance of having at least one of the CAR cards. The player should be indifferent to a $2,000 surrender value if the car had a value of $15,263.16. Any new car is going to be worth more than that.
The following are the indifference points on the value of the car, according to how many unturned cards the player has.
Spelling Bee — Probability of Winning
| Cards | Indifference Point |
|---|---|
| 2 | $15,263.16 |
| 3 | $8,066.23 |
| 4 | $6,849.11 |
| 5 | $6,803.75 |




