Ask The Wizard #351
What do you think of this strategy in roulette:
- Bet two units on black
- Bet one unit on the third column
The beauty of this strategy is there are 8 red numbers and 4 black numbers in the third column. Of the 16 red numbers, half are on columns 1 or 2 and half are on column 3. Let’s ignore the 0 and 00 for now. When the ball lands in red, 8 out of the 18 red numbers are in the third column. If the probability of winning is 8/18 and wins pay 2 to 1, I have a player advantage of 33.3%. Even if we average that with the bet on black with 0% house edge, again ignoring 0 and 00 for now, I still have a 16.7% player advantage. Mixing in the 0 and 00, isn’t my advantage (2/38)*-100% + (36/38)*16.7% = 10.53%! What do you think?
I agree that the conditional advantage of the third column bet is 33.3%, assuming the ball lands in red, and ignoring both zeroes. However, by the same logic, if the ball lands in black, the probability of the third column bet winning is 4/18 = 2/9. A bet with a 2/9 chance of winning that pays 2 to 1 would have a house advantage of 33.33%. So, looking at it your way, the third column bet would have a player advantage of 33.33% half the time and a house edge of 33.33% the other half. Cancelling each other out, that bet has 0% house edge. Finally, mix in the two zeros and the overall player edge is (2/38)*-100% + (36/38)*0% = -5.26%.
Looking at it another way, the following table shows the number of ways all possible outcomes can occur, the probability, units won, and the contribution to the return. The lower right cell shows an an expected loss of -0.105263 units. Divided by the two units bet, that comes to a house edge of 5.26%.
Bohemia Strategy
| Event | Pays | Numbers | Probability | Return |
|---|---|---|---|---|
| 0, 00 | -2 | 2 | 0.052632 | -0.105263 |
| Red & column 1 or 2 | -2 | 10 | 0.263158 | -0.526316 |
| Red & column 3 | 1 | 8 | 0.210526 | 0.210526 |
| Black & column 1 or 2 | 0 | 14 | 0.368421 | 0.000000 |
| Black & column 3 | 3 | 4 | 0.105263 | 0.315789 |
| Total | 38 | 1.000000 | -0.105263 |
In Las Vegas casinos, the chip colors are well known for $100 and under, as follows:
- $1 = White or blue
- $5 = Red
- $25 = Green
- $100 = Black
My question is what are the colors for chips beyond $100?
Most casinos use purple for $500 and yellow for $1,000. Beyond that, things are not as standard. It is easy to say that orange and brown are popular, but not everybody follows that convention. Sometimes you see white and blue reemerge. You might say those colors were already used for $1 chips, but the chip sizes get bigger at a certain point, usually at $1,000. The following table shows what I do know.
Chip Colors
| Casino | $5,000 | $25,000 | $100,000 |
|---|---|---|---|
| Resorts World | Brown | Orange | |
| Cosmopolitan | White | Orange | |
| Treasure Island | White | ||
| Palazzo/Venetian | Brown | Orange | Grey/brown |
| Green Valley Ranch | Brown | ||
| Circa | Orange | ||
| Wynn | White/red | Brown | |
| Bellagio | White | Orange | Steel blue |
| Golden Nugget | Red, white and blue |









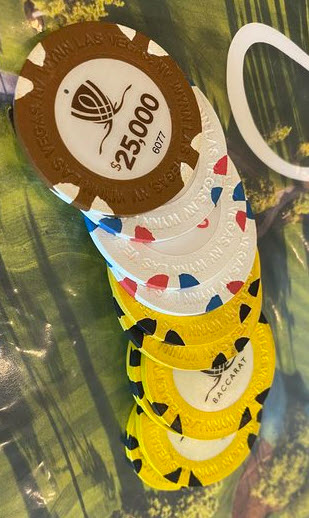
I would like to thank Mdawg for his help with this question and the pictures.
This question is asked and discussed in my forum at Wizard of Vegas.
Did you see this video of a player who correctly called the flop, turn, and river in Texas Hold 'Em? What are the odds?
On the flop, the player calls out 8-9-10. Note that he doesn't specify the suits. All he knows is he folded a jack and queen. The number of ways an 8, 9, and 10 can appear on the flop is 4*4*4 = 64. There are 50 unknown cards left in the deck. The number of ways to choose three cards out of 50 is combin(50,3) = 19,600. So, the probability of getting the flop right was 64/19,600 = 1 in 306.25.
On the turn, there are 47 unknown cards left in the deck. He correctly guesses the four of spades, which had a 1 in 47 chance of being right.
On the river, there are 46 unknown cards left in the deck. He correctly guesses the two of hearts, which had a 1 in 46 chance of being right.
The probability of getting all three predictions right was (46/19600) × (1/47) × (1/46) = 1 in 662,113.
What do I personally think? Just dumb luck. I have seen incorrect predictions at the gambling tables all the time. Do you think anyone makes a YouTube video of the millions of incorrect predictions that were quickly forgotten? In other words, I'm underwhelmed.




