Ask The Wizard #341
What is the expected number of rolls of two dice to achieve every total from 2 to 12? Please use calculus for your solution.
Recall the probability of rolling a total of 2 is 1/36. In t rolls the expected rolls with a total of 2 is t/36. Assume the time between rolls is distributed exponentially with a mean of t/36. The Poisson distribution tells us the probability of zero rolls with a total of 2 is exp(-t/36).
Recall the probability of rolling a total of 3 is 2/36 = 1/18. By the same logic, the Poisson distribution tells us the probability of zero rolls with a total of 3 is exp(-t/18).
Recall the probability of rolling a total of 4 is 3/36 = 1/12. By the same logic, the Poisson distribution tells us the probability of zero rolls with a total of 4 is exp(-t/12).
Recall the probability of rolling a total of 5 is 4/36 = 1/9. By the same logic, the Poisson distribution tells us the probability of zero rolls with a total of 5 is exp(-t/9).
Recall the probability of rolling a total of 6 is 5/36. By the same logic, the Poisson distribution tells us the probability of zero rolls with a total of 6 is exp(-5t/36).
Recall the probability of rolling a total of 7 is 6/36 = 1/6. By the same logic, the Poisson distribution tells us the probability of zero rolls with a total of 7 is exp(-t/6).
The probabilities for 8 to 12 are the same as for 2 to 6.
Thus, the probability that in t units of every total has been rolled at least once is:
(1-exp(-t/36))^2 * (1-exp(-t/18))^2 * (1-exp(-t/12))^2 * (1-exp(-t/9))^2 * (1-exp(-5t/36))^2 * (1-exp(-t/6))
The probability at least total has NOT been rolled in t units of time is 1 - (1-exp(-t/36))^2 * (1-exp(-t/18))^2 * (1-exp(-t/12))^2 * (1-exp(-t/9))^2 * (1-exp(-5t/36))^2 * (1-exp(-t/6))
To get the expected time without at least one total we integrate the function above from 0 to infinity.
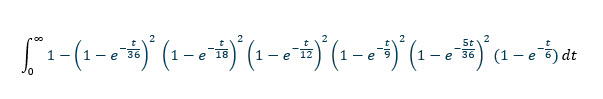
An integral calculator (I recommend this one) will easily solve this as 769767316159/12574325400 = apx. 61.2173847639572 rolls.
This question is asked and discussed in my forum at Wizard of Vegas.
Roll two dice, a red die and a blue die, over and over. Keep track of the sum of rolls for each die. What is the expected number of roles until these two cumulative totals are equal?
It is hard to explain why the answer is infinity. To make matters more confusing and paradoxical, the probability the totals ever being equal is 1.
The following table shows the probability the totals will be the same for the first time after 1 to 16 rolls.
Probability Equal Totals for First Time
| Rolls | Probability |
|---|---|
| 1 | 0.166667 |
| 2 | 0.112654 |
| 3 | 0.092850 |
| 4 | 0.080944 |
| 5 | 0.072693 |
| 6 | 0.066539 |
| 7 | 0.061722 |
| 8 | 0.057819 |
| 9 | 0.054573 |
| 10 | 0.051819 |
| 11 | 0.049443 |
| 12 | 0.047367 |
| 13 | 0.045532 |
| 14 | 0.043895 |
| 15 | 0.042423 |
| 16 | 0.041089 |
Excel shows a very close fit to this curve is y = 0.1784*x-1.011, where x = number of rolls and y = probability.
The sum of this infinite series is infinity.
This question is asked and discussed in my forum at Wizard of Vegas.
What is the breakeven jackpot for the Pennsylvania Cash 5 game? You may ignore taxes and jackpot sharing.
First, let's go over the rules. The bet cost is $2. The game is based on drawing five balls out of 43. Here is the pay table:
- Match 5 = Jackpot
- Math 4 = $200
- Match 3 = $10
- Match 2 = $2
In addition, the player gets what I presume is like a scratch-off card. This has a 1/80 chance of paying $6 and 1/5 chance of paying $2.
The following table shows my analysis of the base game. It shows the value of catching 2 to 4 numbers is $0.287784.
Cash 5 Return Table
| Catch | Pays | Combinations | Probability | Return |
|---|---|---|---|---|
| 5 | jackpot | 1 | 0.000001 | ? |
| 4 | 200 | 190 | 0.000197 | 0.039477 |
| 3 | 10 | 7030 | 0.007303 | 0.073032 |
| 2 | 2 | 84360 | 0.087638 | 0.175276 |
| 1 | 0 | 369075 | 0.383416 | 0.000000 |
| 0 | 0 | 501942 | 0.521445 | 0.000000 |
| Total | 0 | 962598 | 1.000000 | 0.287784 |
The following table shows my analysis of the Quick Cash instant win feature. The lower right cell shows a value of $0.475
Instant Cash Return Table
| Catch | Pays | Probability | Return |
|---|---|---|---|
| 6 | 1 | 0.012500 | 0.075000 |
| 2 | 16 | 0.200000 | 0.400000 |
| 0 | 63 | 0.787500 | 0.000000 |
| Total | 80 | 1.000000 | 0.475000 |
Thus, the value of the non-progressive prizes is $0.287784 + $0.475000 = $0.762784.
Let j equal the value of the breakeven jackpot. Then:
2 = 0.762784 + j × (1/962598)
1.237216 = j × (1/962598)
j = 1.237216 × 962598
j = $1,190,941.95.
The overall rate of return is 0.381392 plus 0.051943 for every $100,000 in the jackpot.
As stated in the question, all this ignores taxes and jackpot sharing.
This question is asked and discussed in my forum at Wizard of Vegas.




