Ask The Wizard #336
The Morongo casino in southern California is running a promotion where they pay a bonus of $16 if the dealer is dealt a hard 16. What is the value of this?
This is a good one for the player! Their web site doesn’t elaborate on the details so I’m going to assume it is for the initial two cards only. I see my from an old Current Blackjack Newsletter from October 2018, most tables have the following rules:
- Dealer hits soft 17
- Six decks
- Blackjack pays 3 to 2
- Double after split allowed
- Re-splitting aces allowed
My blackjack house edge calculator says these rules have a house edge of 0.55% with a continuous shuffler and 0.57% with a cut card.
Regardless of the rules, the probability of a hard 16 in the first two cards is 6.51%. Getting $16 with a 6.51% chance is worth $1.04 per hand. I’m going to assume a minimum bet of $25 because most casinos are raising their minimums in this era of the coronavirus. Not counting the bonus, the expected loss per hand is $0.14 at a $25 bet. That makes the expected win per hand $1.04 - $0.14 = $0.90. Relative to the bet amount, that is a player advantage of 3.59%!
If we assume a good case scenario of playing three hands of $25 at 80 rounds per hour, that would be an expected hourly win of $216!
This question is asked and discussed in my forum at Wizard of Vegas.
There is a 5x5 pegboard and 3 pegs. What is the probability that three randomly placed pegs form a triangle?
First, there are combin(25,3) = 2,300 possible combinations for the pegs.
How many of those combinations form a triangle? Let’s use this board to help:
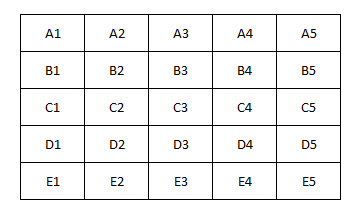
First, there are five rows, five columns, and two diagonals. For any one of them there are combin(5,3) = 10 ways to place the pegs in a line. So there are 12*10 = 120 combinations that way.
Second, there are four ways to connect the center square of a row/column to a center square of an adjacent row/column. In other words, these three placements:
- A3, B4, C5
- C5, D4, E3
- E3, D2, C1
- C1, B2, A3
So, now we’re at 120 + 4 = 124
Third, there are four different diagonal lines that are four spaces:
- A2, B3, C4, D5
- B5, C4, D3, E2
- E4, D3, C2, B1
- D1, C2, B3, A4
For each of them there are combin(4,3)=4 ways to place three pegs. So that adds 4*4 = 16 more.
We are now at 124+16 = 140
Fourth, consider the way knights move in chess, in a 2x1 L shape. For each corner there are two ways a knight can move. In all of them the knight may move again in the same line formed the first move. So that is 4*2 = 8 more:
- A1, C2, E3 A1, B3, C5
- A5, B3, C1
- A5, C4, E3
- E5, C4, A3
- E5, D3, C1
- E1, D3, C5
- E1, C2, A3
There are also four such knight lines that go through the center:
- A2, C3, E4
- A4, C3, E2
- B5, C3, D1
- D5, C3, B1
Adding the 12 knight lines, we are at 140+12= 152
If there are 2,300 total combinations and 152 form lines, then 2300-152 = 2,148 don’t form lines and thus form triangles.
Thus, our answer is 2,148/2,300 = 93.39%.
This question is asked and discussed in my forum at Wizard of Vegas.
I found a 4-deck Spanish 21 game that paid 3-2 on an ace/10 after splitting. How much is that rule worth?
For the sake of simplicity, let’s assume re-splitting aces is not allowed. Also recall that Spanish 21 uses 48-card Spanish decks with no 10’s. Finally, recall that 21 points is an automatic winner in Spanish 21.
Even without that rule, the player should always split aces. The probability of getting a pair of aces in a four Spanish-deck game is combin(16,2)/combin(192,2) = 120/18336 = 0.65%.
The probability each ace will get a 10 is (4*12)/(48*12-2) = 48/190 = 25.26%. With two aces, the expected number that will turn into blackjacks is 2*48/190 = 96/190 = 0.5053.
Each blackjack will be worth an extra half unit. Thus, the value of this rule is (120/18336)*(96/190)*(1/2) = 0.17%.
Even with this rule, the player should still not split tens, so we don’t need to worry about that. So, this rule lowers the house edge by 0.17%.
How many unique rectangles exist for which the number of tiles on the perimeter are equal to the number of tiles on the inside?
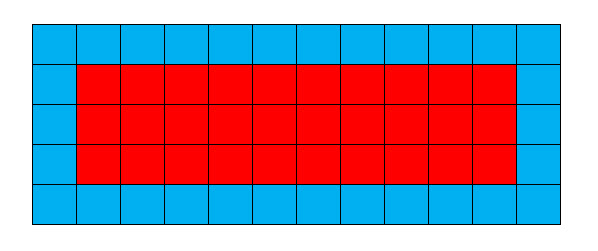
Let’s let x and y be the dimensions of the INNER rectangle.
The area of that rectangle is x*y.
The area of the perimeter is 2x + 2y + 4
It is given that xy = 2x+2y+4
xy-2x = 2y + 4
x(y-2) = 2y+4
x=(2y+4)/(y-2)
y must be greater or equal to 3. Let’s see what x is for some y values equal or greater than 3.
If y = 3, then x = 10
If y = 4, then x = 6
If y = 5, then x = 14/3
If y = 6, then x=4
So, 3x10 and 4x6 are solution. 6x4 is not, because it is not a unique solution. As y gets bigger, x will get smaller. Much like y must be equal or greater than 3, so must x. There is only one more possible value for x as it is going down as y goes up, which is x=3. However, if x=3, then y=10, and that is no unique either.
So the answer is 2: 3x10 and 4x6 for the inside rectangle. If you prefer to count solutions by the outer rectangle, they would be 5x12 and 6x8.
This question is asked and discussed in my forum at Wizard of Vegas.




