Ask The Wizard #326
What is the Iron Cross strategy in craps and what do you think of it?
The Iron Cross is a way of betting the field and place bets to win on any roll of the dice except a 7. The field already covers the 2, 3, 4, 9, 10, 11, and 12. The player will add to that place bets on the 5, 6, and 8 to cover the rest of the numbers, besides 7. The following table shows what the math looks like with a $5 field bet, $5 place bet on the 5, and $6 place bets on the 6 and 8.
Iron Cross
| Dice Total | Win | Combinations | Probability | Return |
|---|---|---|---|---|
| 2 | 10 | 1 | 0.027778 | 0.277778 |
| 3 | 5 | 2 | 0.055556 | 0.277778 |
| 4 | 5 | 3 | 0.083333 | 0.416667 |
| 5 | 2 | 4 | 0.111111 | 0.222222 |
| 6 | 2 | 5 | 0.138889 | 0.277778 |
| 7 | -22 | 6 | 0.166667 | -3.666667 |
| 8 | 2 | 5 | 0.138889 | 0.277778 |
| 9 | 5 | 4 | 0.111111 | 0.555556 |
| 10 | 5 | 3 | 0.083333 | 0.416667 |
| 11 | 5 | 2 | 0.055556 | 0.277778 |
| 12 | 15 | 1 | 0.027778 | 0.416667 |
| 36 | 1.000000 | -0.250000 |
The lower right cell of the table shows an expected loss of $0.25. The total amount bet is $22. This makes the overall house edge $0.25/$22 = 1/88 = 1.14%.
At this point you may be wondering how this house edge can be lower than the house edge of each individual bet. The answer is because the house edge of 1.52% placing the 6 and 8 and 4.00% placing the 5 is based on per bet resolved. If define the house edge on place bets on a per roll basis, then the house edge placing the 6 or 8 is 0.46% and on the 5 is 1.11%.
We can get at the 1.14% house edge by taking a weighted average of all bets made, as follows:
($5*2.78% + $5*1.11% + $12*0.46%)/22 = $0.25/$22 = 1.14%.
Be wary of casinos that pay only 2 to 1 for 12 on the field bet. Insist on getting the full 3 to 1. The short pay doubles the house edge on that bet from 2.78% to 5.56%.
As to my opinion, compared to most games, 1.14% is a pretty good bet. However, you could do much better in craps. For example, with 3-4-5x odds, making the pass and come bets, with full odds, you can get the house edge down to 0.37%. Doing the opposite, betting the don't pass and don't come, plus laying full odds, results in a house edge of 0.27%.What is the expected number of rolls of a fair die to roll every face at least twice?
While this could be solved with a long and tedious Markov chain, I prefer an integral solution. I explain how to use this method in my pages on the Fire Bet and Bonus Craps.
Imagine that instead of significant events being determined by the roll of the die, one at a time, consider them as an instant in time. Assume the time between events has a memory-less property, with an average time between events of one unit of time. In other words, the time between events follows an exponential distribution with a mean of 1. This will not matter for purposes of adjudicating the bet, because events still happen one at a time.
Per the Poisson distribution, the probability that any given side of the die has been rolled zero times in x units of time is exp(-x/6)*(x/6)0/0! = exp(-x/6). Poisson also say the probability of any given side being rolled exactly once is exp(-x/6)*(x/6)1/1! = exp(-x/6) * (x/6). Thus probability any side has been rolled two or more times in x units of time is 1 - exp(-x/6)*(1 + (x/6)). The probability that all six sides have been rolled at least twice is (1 - exp(-x/6)*(1 + (x/6)))6. The probability that at least one side has not been rolled at least twice is equal to:
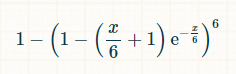
We need to integrate that over all time to find how much time will go by, on average, where the desired goal has not been achieved.
Fortunately, we can use an integral calculator at this point. For the one linked to, put 1- (1 - exp(-x/6)*(1 + x/6))^6 dx = apx. 24.1338692 in the text box following "Calculate the integral of" and under custom, set the bound of integration from 0 to ∞.
The answer is 390968681 / 16200000 = apx. 24.13386919753086
This question is asked and discussed in my forum at Wizard of Vegas.
I have a two-part question.
For part 1, given:- x + y + z = 1
- x^2 + y^2 + z^2 = 4
- x^3 + y^3 + z^3 = 9
What is x^4 + y^4 + z^4 ?
For the second part, what is the answer to the general case when:
- x + y + z = a
- x^2 + y^2 + z^2 = b
- x^3 + y^3 + z^3 = c
Question 1: 97/6 = apx. 16.166666
Question 2: a4/6 + (4/3)ac - a2b + b2/2
For see my solution (PDF)
This question is raised and discussed in my forum at Wizard of Vegas.
You start with a fair 6-sided die and roll it six times, recording the results of each roll. You then write these numbers on the six faces of another, unlabeled fair die. For example, if your six rolls were 3, 5, 3, 6, 1 and 2, then your second die wouldn’t have a 4 on it; instead, it would have two 3s.
Next, you roll this second die six times. You take those six numbers and write them on the faces of yet another fair die, and you continue this process of generating a new die from the previous one.
Eventually, you’ll have a die with the same number on all six faces. What is the average number of transitions from one die to another (or total rolls divided by 6) to reach this state?
Let's label the initial die with letters instead of numbers, to avoid confusion. Let's label each possible die state with letters. For example, AAABBC would mean three of one letter, two of another, and one of a third. The initial state would obviously be ABCDEF.
Let E(ABCDEF) be the expected number of rolls from state ABCDEF.
E(ABCDEF) = 1 + [180 × E(AAAAAB) + 450 × E(AAAABB) + 300 × E(AAABBB) + 1800 × E(AAAABC) + 7200 × E(AAABBC) + 1800 × E(AABBCC) + 7200 × E(AAABCD) + 16200 × E(AABBCD) + 10800 × E(AABCDE) + 720 × E(ABCDEF)]/46656Building on the number of combinations of going from one state to another, the following transition matrix shows how many ways there are for going from each initial state (left column) to each new state. This took a few hours to construct properly, by the way.
Transition Matrix A
| State Before |
AAAAAA | AAAAAB | AAAABB | AAABBB | AAAABC | AAABBC | AABBCC | AAABCD | AABBCD | AABCDE | ABCDEF |
|---|---|---|---|---|---|---|---|---|---|---|---|
| AAAAAB | 15,626 | 18,780 | 9,750 | 2,500 | - | - | - | - | - | - | - |
| AAAABB | 4,160 | 13,056 | 19,200 | 10,240 | - | - | - | - | - | - | - |
| AAABBB | 1,458 | 8,748 | 21,870 | 14,580 | - | - | - | - | - | - | - |
| AAAABC | 4,098 | 12,348 | 8,190 | 2,580 | 7,920 | 10,080 | 1,440 | - | - | - | - |
| AAABBC | 794 | 5,172 | 8,670 | 5,020 | 6,480 | 17,280 | 3,240 | - | - | - | - |
| AABBCC | 192 | 2,304 | 5,760 | 3,840 | 5,760 | 23,040 | 5,760 | - | - | - | - |
| AAABCD | 732 | 4,464 | 4,140 | 1,680 | 7,920 | 14,400 | 2,520 | 4,320 | 6,480 | - | - |
| AABBCD | 130 | 1,596 | 3,150 | 1,940 | 5,280 | 16,800 | 3,600 | 4,800 | 9,360 | - | - |
| AABCDE | 68 | 888 | 1,380 | 760 | 3,960 | 11,520 | 2,520 | 7,200 | 14,040 | 4,320 | - |
| ABCDEF | 6 | 180 | 450 | 300 | 1,800 | 7,200 | 1,800 | 7,200 | 16,200 | 10,800 | 720 |
I won't go into a long lecture on matrix algebra, except to say let's say matrix B is as follows:
Matrix B
| State Before |
AAAAAB | AAAABB | AAABBB | AAAABC | AAABBC | AABBCC | AAABCD | AABBCD | AABCDE | ABCDEF |
|---|---|---|---|---|---|---|---|---|---|---|
| AAAAAB | -27876 | 9750 | 2500 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| AAAABB | 13056 | -27456 | 10240 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| AAABBB | 8748 | 21870 | -32076 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| AAAABC | 12348 | 8190 | 2580 | -38736 | 10080 | 1440 | 0 | 0 | 0 | -46656 |
| AAABBC | 5172 | 8670 | 5020 | 6480 | -29376 | 3240 | 0 | 0 | 0 | -46656 |
| AABBCC | 2304 | 5760 | 3840 | 5760 | 23040 | -40896 | 0 | 0 | 0 | -46656 |
| AAABCD | 4464 | 4140 | 1680 | 7920 | 14400 | 2520 | -42336 | 6480 | 0 | -46656 |
| AABBCD | 1596 | 3150 | 1940 | 5280 | 16800 | 3600 | 4800 | -37296 | 0 | -46656 |
| AABCDE | 888 | 1380 | 760 | 3960 | 11520 | 2520 | 7200 | 14040 | -42336 | -46656 |
| ABCDEF | 180 | 450 | 300 | 1800 | 7200 | 1800 | 7200 | 16200 | 10800 | -46656 |
The answer is the determinant of matrix B to that of matrix A:
Determ(A) = 1,461,067,501,120,670,000,000,000,000,000,000,000,000,000,000
Determ(B) = 14,108,055,348,203,100,000,000,000,000,000,000,000,000,000,000
Determ(B) / Determ(A) = apx. 9.65599148388557




