Ask The Wizard #292
Is it true that the D casino took out their 101.60% Loose Deuces game? I recall you saying that was the loosest video poker machine in Vegas. If the rumors are true, which machine is number one now?
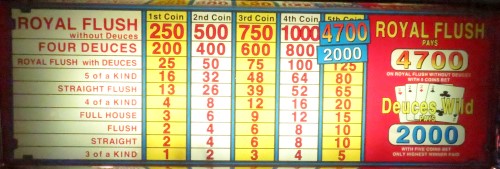
Yes, that machine is no longer. As you point out, the previous number two game now bubbles up to the number one spot. That is a 100.92% Double Deuces game at the El Cortez. The full pay table is 940-400-25-16-13-4-3-2-2-1. It can be found on the slot room on the north end of the casino full of old cathode raw machines. Here is a picture of me standing next to it.

In case you're wondering, the difference between Loose Deuces and Double Deuces is the former pays 500 for four deuces and the latter 400.
I heard there was a woman in the United Kingdom who gave birth to her first and second children on exactly the same dates as Prince George and Princess Kate. What are the odds of that?
I'll have to make some rough assumptions to answer this one.
To review, Prince George was born on July 22, 2013 and Princess Charlotte on May 2, 2015. That is a difference of 649 days. If we allow for a nine-month gestation, that is 379 days between the birth of George and the conception of Charlotte.
Just going off of personal observation, let's assume the mean time between siblings is three years. That would mean 825 days between birth and conception of the next child. Using the exponential distribution, I find the probability of a difference of exactly 379 days is 0.0442%.
Next, let's assume that any female between the ages of 20 and 39 is a potential candidate. According to Wikipedia, the population of the United Kingdom in that age range is 16,924,000. Let's divide that by two to get rid of the men for 8,462,000 women of childbearing age in the UK.
The fertility rate in the United Kingdom, which is the average number of children born to each woman of childbearing age, is 1.92. Using the Poisson distribution, I find the probability of two or more children is 69.83%. So, the number of women in the UK of childbearing age who will have two or more children is 8,462,000 × 69.83% = 5,909,015.
Since women generally have children closer to age 20 than 40, let's roughly say that the mother's age at the time of the first born will be evenly distributed between the ages of 20 and 37. So, the number of women who will have their first child in the UK on exactly the birthday of Prince George is 5,909,015/(17×365) = 952.32.
We already established that the probability of an exact age difference between the first and second child of 379 days is 0.0442%. Thus, the expected number of women who had their second child on exactly the same day Princess Charlotte was born, who already had their first born on the exact day Prince George was born, is 952.32 × 0.000442 = 0.421.
Using the exponential distribution, given a mean of 0.421, the probability of at least one woman having her first and second children on the exact same days as Prince George and Princess Charlotte were born is 34.36%.
By the way, I find the probability of the same thing in the United States is 86.32%.
Is it illegal to play on another person's player card?
I can speak only to Nevada, where I believe the answer is no. However, that doesn't mean the casinos like it. I know of a case where someone was trespassed for letting a friend use her card to collect free play. They seem to be more lenient if it is done at table games for the purpose of earning comp points.
I have heard in Pennsylvania it is illegal to use another person's player card but can't confirm this.
This question is discussed in my forum at Wizard of Vegas.
On a recent trip to Reno I noticed these two signs.
 |
 |
How does the total amount paid out or won correlate to how loose the slots are? In other words, should I prefer to play at the Circus Circus and Reno airport because their slots allegedly pay out so much?
No. To get an estimate of how loose a casino's slots are you would want to know the ratio of money returned to money bet. This ratio would typically be about 92%. Telling you only the amount paid out is not useful at all. Consider the Circus Circus claim of paying out $26 million a month. They don't disclose how much players bet to get that $26 million. What if they bet $35 million? That would be a return of 71.43%, which would be awful.
In conclusion, I don't know whether to be angry over what I consider to be deceptive advertising or depressed that people fall for it.
Congratulations on your 50-mile unicycle ride challenge for your 50th birthday! Now that you can cross that one off your list, what are some other challenges still on it?
Thank you for asking. For the benefit of other readers, I challenged myself to ride a unicycle 50 miles within eight hours by my 50th birthday. I am proud to say that I achieved it! In fact, 53 miles in 7.5 hours. I have a very long and boring video about it.
To answer your question, high on my list is to do the Fargo Street challenge on a unicycle. For those who don't know, Fargo Street is the steepest street in Los Angeles and second steepest in the United States. I already easily did it on a bicycle on July 18 as a test run and made a video of that.
Besides that, here are some other challenges on my bucket list:
- Climb Mount Rainier
- Climb Mount Adams
- Climb Pico de Orizaba
- Climb Mount Aconcagua
- Clinb Mount Kilimanjaro
- Hike the John Muir Trail
- Hike the Appalachian Trail
- Unicycle the Camino de Santiago.
- Unicycle New Zealand (from north to south)
The next to be completed should be Mount Rainier and Pico de Orizaba after that. Here are some peaks I have already climbed.
Let x be a random number uniformly distributed between 0 and 1.
Let y be a random number uniformly distributed between 0 and 2.
Let z be a random number uniformly distributed between 0 and 3.
What is the probability of each of these:
- a<b
- a<c<b
- b<a<c
- b<c<a
- c<a<b
- c<b<a
Scroll down 100 lines for the answer.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
- a<b<c: 4/9
- a<c<b: 7/36
- b<a<c: 7/36
- b<c<a: 1/36
- c<a<b: 1/9
- c<b<a: 1/36
Scroll down another 100 lines for the solution.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
The probability that each number will fall in the following ranges are all equally likely at 1/6 each.
0<x<1, 0<y<1, 0<z<1
0<x<1, 0<y<1, 1<z<2
0<x<1, 0<y<1, 2<z<3
0<x<1, 1<y<2, 0<z<1
0<x<1, 1<y<2, 1<z<2
0<x<1, 1<y<2, 2<z<3
Given each of these possible ranges, the following table shows the probability of each possible ordering:
Since each set of ranges is equally likely, we multiply the total row by 1/6 to get the following answers:
- a<b<c: 4/9
- a<c<b: 7/36
- b<a<c: 7/36
- b<c<a: 1/36
- c<a<b: 1/9
- c<b<a: 1/36
This question was asked and discussed in my forum at Wizard of Vegas.
What is your opinion of Casino Patron Charities?
Let me tell you why I think it is a great idea. Sometimes when I visit the supermarket I get asked at the checkout if I would like to make a donation to whatever charity they are promoting. Usually they say, "Would you like to donate a dollar to (insert name of charity here)?" However, I prefer it when they let me select my own donation. This is a convenient way for me to not have to fuss with any change that I will just add to my five-gallon water jug of loose change, which I have been using to hoard loose change for years. So, if I owe $25.43, for example, I'll make a donation of 57 cents. That is always initially met with an odd look and maybe a sarcastic remark. However, most of the time the cashier will realize that I just added whatever amount I needed to get to a total evenly divisible by one dollar. Of course, I look like a real cheap bastard when this amount is just a few pennies, but I am very set in my ways.
So, imagine my pleasure when I found somebody else had thought of the same idea, except based on slot vouchers. The concept is by Howard VanBooven who created Casino Patron Charities. The way it works is when you put a voucher in the redemption machine you will be prompted whether you wish to donate the loose change to charity. This is a great idea for a few reasons:
- Patrons like me who hate change can donate the coins they don't really want to fuss with anyway. Hopefully earning a few karma points in the process.
- The charities will benefit with the donations.
- Hopefully there won't be so many pesky vouchers laying about for a few cents. These vouchers also attract vagrants who prowl around the casinos collecting them.
In closing, I applaud the idea and hope to see it implemented around Las Vegas soon.