Ask The Wizard #270
I play at a casino that allows you to split pairs an unlimited number of times. What is the effect of this rule?
I show the value of infinite re-splitting, compared to splitting up to a maximum of four hands, is worth 0.05% if the rule applies to all pairs, including aces, and 0.02% if it does not include aces. This question was raised and discussed in the forum of my companion site Wizard of Vegas.
Apparently the LVH has a $10 ticket out for VCU to win the national championship at 5000:1. That would pay $50,000 should VCU win. *IF* you held the ticket, what is the minimum you would you accept in trade at this point? (final 4 beginning tomorrow)
I see that at Pinnacle the lines on VCU to win the championship are: Yes +604 No -750 Let’s figure out how much you would have to bet against VCU winning to lock in an equal win either way, and what that win would be. Let x bet the bet. Win outcome = 50,000 - x
Lose outcome = x*(100/750) = (2/15)x Set these equal to each other 50000-x = (2/15)x 50000 = (17/15)x x = 50000×(15/17) x = $44,117.65 Let see if that is right... If VCU wins the out come $50,000 minus from the Hilton minus $44,117.65 to Pinnacle = $5,882.35 If VCU doesn’t win you don’t get anything from the Hilton, but the Pinnacle bet will pay $44,117.65 × (100/750) = $5,882.35. However, the bet against VCU I doubt pays fair odds. If the owner was extremely risk averse, and was eager to sell the ticket, then I think about $6,000 would be a fair. However, I would base the probability of VCU winning on the +604 line that they will win, implying a 100/704 = 14.2% chance. That would make the value of the ticket about $7,100. This all ignores the tax implications. This question was raised and discussed in the forum of my companion site Wizard of Vegas.
What is the best hand you can get in pai gow poker when not banking?
There doesn’t seem to be any unbeatable hand when not banking. So let’s consider two hands. The first can’t be beaten or tied in the high. The second can’t be beaten or tied in the low.
(1) AAAAW/KK (W=wild)
The five aces cannot be beaten in the high, but the pair of kings could be tied in the low. The number of combinations with two kings is combin(44,5) = 1,086,008. The number of total combinations of 7 cards out of the 46 left is 53,524,680. So the probability of two kings is 1,086,008/53,524,680 = 2.03%. With many of those combinations the dealer will not play the KK in the low. According to my Pai Gow Poker Appendix 1, the dealer will have a pair of aces or less in the high 74.93% of the time. That means he will make a two pair or better, allowing him to play the kings in the low, 25.07% of the time. So the probability the player will get two kings, and be able to play them in the low, is 2.03% × 25.07% = 0.51%, or 1 in 196.
(2) AWQJT (suited)/AA
The royal can be tied in the high, but the aces cannot be beaten or tied in the low. Here I’m using the wild to substitute for a king to make a royal, but it could also have substituted for the Q, J, or T. I don’t want it to substitute for an ace, because then there would be two aces left in the deck for the dealer to tie the low. This way, the dealer can only tie the high with another royal. What are the odds of that? There are three suits left for the royal, and the other two cards could be anything. So the number of combinations that push is 3×combin(41,2) = 2,460. I get the 41 from 46 cards left in the deck after the player removed 7 from the original 43, and then subtract 5 more for the 5 cards in the dealer’s royal. We have combin(46,7) = 53,524,680 in the denominator. So the odds of a tie with wild royal/AA is 2,460/53,524,680 = 0.004596%, or 1 in 21,758.
Before some perfectionist writes to me, there may be some bizarre situations where the dealer doesn’t play the hand the way I intended. I’m not looking to get an exact probability of each situation, but to substantiate why I think wild royal/AA is the best hand you can get in pai gow poker when not banking.
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
What ratio of genes would I have in common with a full brother or sister, other than identical twin?
1/2.
If we used keno as a comparison, everybody would have 40 genes, each represented by a keno ball. However, each ball would have unique number. When two people, who are not related, mate it is like combining 80 balls between the two of them into a hopper, and randomly choosing 40 genes for the offspring of the mating.
So when you were conceived, you got half the balls in the hopper, and the other half were wasted. When your brother or sister was conceived he/she got half from the balls drawn when you were born, and half that were not drawn. So you are 50% genetically identical. Much for the same reason that if 40 numbers were drawn in keno, two consecutive draws would average 20 balls in common.
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
A factory that produces tables and chairs is equipped with 10 saws, 6 lathes, and 18 sanding machines. It takes a chair 10 minutes on a saw, 5 minutes on a lathe, and 5 minutes of sanding to be completed. It takes a table 5 minutes on a saw, 5 minutes on a lathe, and 20 minutes of sanding to be completed. A chair sells for $10 and a table sells for $20. How many tables and chairs should the factory produce per hour to yield the highest revenue, and what is that revenue?
Let’s let c stand for the number of chairs made per hour, and t the number of tables. Revenue per hour will be 10×c + 20×t.
The 10 saws result in 600 minutes of sawing per hour. We were given that it takes a chair 10 minutes of saw time, and a table 5. So that limits hour hourly production to:
(1) 10c + 5t <= 600
The 6 lathes result in 360 minutes of lathing per hour. We were given that it takes a chair 5 minutes of saw time, and a table 5. So that limits hour hourly production to:
(2) 5c + 5t <= 360
The 18 sanding machines result in 1080 minutes of sanding per hour. We were given that it takes a chair 5 minutes of saw time, and a table 20. So that limits hour hourly production to:
(3) 5c + 20t <= 1080
The following graph shows the three constraints placed by the three sets of machinery. The factory may produce any combination of chairs and tables that is under all three lines. The question is where under the three lines results in the greatest revenue.
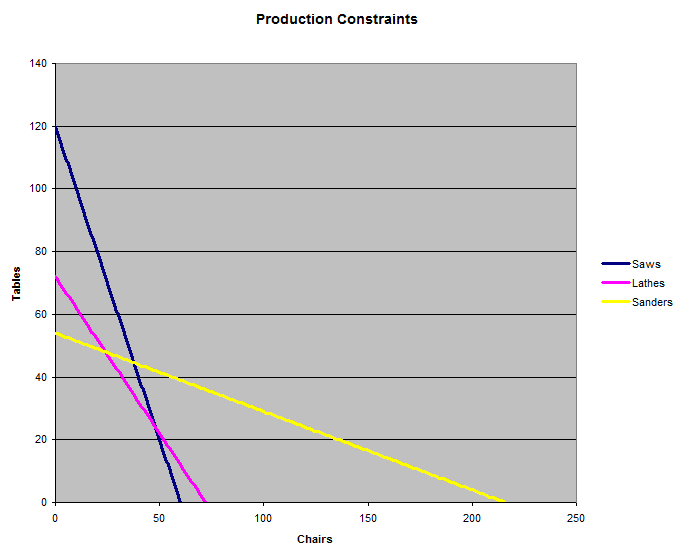
It stands to reason that the answer would be the intersection of two lines, make all chairs, or make all tables. So let’s find where the lines intersect. First, let’s find where equation (1) and (2) intersect. We can change the <= expression to just =, to use the machines to their maximum potential.
(1) 10c + 5t = 600
(2) 5c + 5t = 360
Subtract (2) from (1):
5c = 240
c = 48
Plugging 48 for c into equation (1):
10×48 + 5t = 600
5t = 120
t = 24
So, equations (1) and (2) meet at 48 chairs and 24 tables.
Next, let’s find where equations (2) and (3) meet:
(2) 5c + 5t = 360
(3) 5c + 20t = 1080
Subtracting (2) from (3):
15t = 720
t = 48
Putting that into (2) or (3) we can solve for c, which is 24.
So, equations (2) and (3) meet at 24 chairs and 48 tables.
We don’t need to bother finding where equations (1) and (3) meet, because we can see from the graph that where the saw and sanders lines meet is outside of the lathe constraint.
It is also possible that making chairs only is the right answer. The graph shows that the saws is the biggest limitation to making only chairs. From equation (1) if we put in 0 for the number of tables we get c=60.
Another possibility is making tables only. The graph shows that the sanders will be the biggest limitation. Putting in 0 chairs into equation (3) we find we can make no more than 54 tables.
The following graph shows the total revenue for each viable answer. Remember, the revenue is $10 per chair and $20 per table.
Total Hourly Revenue
| Chairs | Tables | Revenue |
| 0 | 54 | $1,080 |
| 24 | 48 | $1,200 |
| 48 | 24 | $960 |
| 60 | 0 | $600 |




