Ask The Wizard #261

To help answer this question, I graphed average points scored by the week number in the NFL, based on every season from 1983 to 2009. The following graph shows the results.

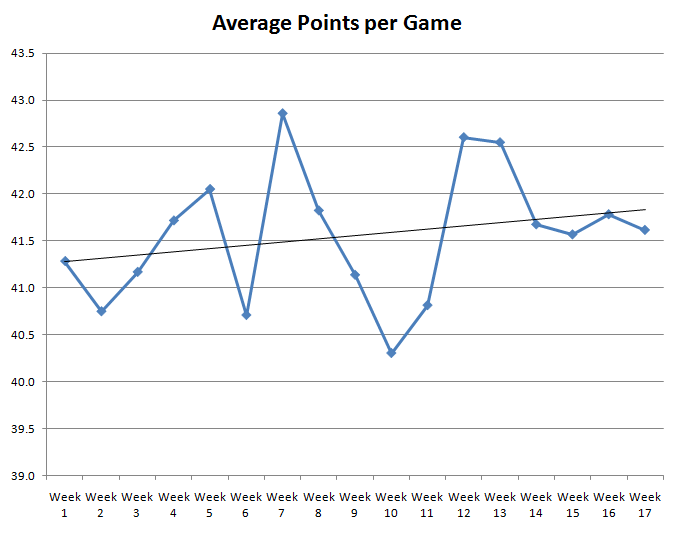
As you can see, the line goes up and down a lot. The thin black line is a least-squared best fit line, which shows a general trend upward. So as the seasons progresses, and temperatures drop, average points scored increases slightly, but that could easily be random variation.

That is about as far as I can take it. For a general opinion about how weather affects sports betting in general, I turned to my friend Jason Been, who is an expert on the topic. Here is what he said:

In most cases, wind is the predominant aspect of weather that most affects a game; but, it is not the only one. In baseball and other outdoor sports, shadows can have an equal affect, especially during early- and late-season baseball afternoon games. Rain or snow isn’t as big of a factor as most people think in football, as it generally affects both the offense and defense equally. An example would be a defensive back against a wide receiver. The rain and snow would slow them down equally, thus giving neither side an edge. Wind can simply eliminate a passing game in football along with kicking. I have seen games where a passing team has been forced to run the ball almost every play due to a strong crosswind. It doesn’t happen often, but on occasion the wind is the ultimate decider of a game.

This question was raised and discussed in the forum of my companion site Wizard of Vegas.

I asked a former table Vegas game manager about this. He said that the portion of the odds bet over the allowed multiple of the line bet would be paid at place bet odds. This question was raised and discussed in the forum of my companion site Wizard of Vegas.

Based on the 2000-2009 NFL seasons, the answer is 57%.

This puzzle is discussed on the BBC show Quite Interesting. Scroll down 100 lines for the answer and solution.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100

Here are my probabilities of A winning according to each initial target. As you can see, A’s probability of winning is maximized by deliberately firing in the air.

Truel Odds

Strategy	Prob. Win
Air	13.887%
A	0.000%
B	12.560%
C	13.094%

For the solution, let’s use the notation Pr(X) to denote the probability of group X, and only group X, remains after a round. Let’s use the terminololy Pr(X*) to denote the probability of group X eventually winning the round, after repeating until the game state changes by somebody getting hit. Let Pr(X**) be the probability that player X is the sole survivor. To find the final probabilities, let’s look at the two-player states first. It is obvious that each will shoot at the other.

A vs. B

• Pr(A) = 0.1
  
• Pr(B) = 0.9×0.6 = 0.54
  
• Pr(AB) = 0.9×0.4 = 0.36

If both survive then they will repeat until there is one survivor only. So the probabilities of being the final survivor are:

• Pr(A*) = Pr(A)/(1-Pr(AB)) = 0.1/0.64 = 0.15625
  
• Pr(B*) = Pr(B)/(1-Pr(AB)) = 0.54/0.64 = 0.84375

A vs. C

• Pr(A) = 0.1
  
• Pr(C) = 0.9×0.9 = 0.81
  
• Pr(AC) = 0.9×0.1 = 0.09

If both survive then they will repeat until there is one survivor only. So the probabilities of being the final survivor are:

• Pr(A*) = Pr(A)/(1-Pr(AC)) = 0.1/0.91 = 0.10989011
  
• Pr(C*) = Pr(B)/(1-Pr(AC)) = 0.81/0.91= 0.89010989

B vs. C

• Pr(B) = 0.6
  
• Pr(C) = 0.4×0.9 = 0.36
  
• Pr(BC) = 0.$×0.1 = 0.04

If both survive then they will repeat until there is one survivor only. So the probabilities of being the final survivor are:

• Pr(B*) = Pr(A)/(1-Pr(BC)) = 0.6/.96 = 0.625
  
• Pr(C*) = Pr(B)/(1-Pr(BC)) = 0.36/.96= 0.375

Now we’re ready to analyze the three-player case. Let’s consider the situation where A aims at B.

Three Player — A Aims at B

If A hits B then C will definitely survive, and may or may not hit A. So two possible outcomes of hitting B are AC and C. If A misses B then B will aim at the greater threat C. If B hits C then A and B will survive. If B misses C then C will aim at the greater threat B. If C misses B then all three will survive. If C hits B then A and C will survive. So the possible outcomes are C, AB, AC, and ABC.

• Pr(A) = 0.
• Pr(B) = 0.
• Pr(C) = 0.1 × 0.9 = 0.09. This is achieved by A hitting B, and then C hitting A.
• Pr(AB) = 0.9 × 0.6 = 0.54. This is achieved by A missing B, and then B hitting C.
• Pr(AC) = 0.1 × 0.1 + 0.9 × 0.4 × 0.9 = 0.334. This can be achieved two ways. The first is A hitting B, and then C missing A. The second is A missing B, B missing C, and then C hitting B.
• Pr(BC) = 0.
• Pr(ABC) = 0.9 × 0.4 × 0.1 = 0.036. This is achieved by all three missing.

By the same logic as the two-player cases, we can divide each outcome by (1-Pr(ABC))=0.964 to find the probabilities of each state, assuming that the state of the game did change after the round.

• Pr(C*) = 0.09/0.964 = 0.093361.
  
• Pr(AB*) = 0.54/0.964 = 0.560166.
  
• Pr(AC*) = 0.334/0.964 = 0.346473.

From the two-player cases, we know if it comes down to A and B then A will win with probability 0.15625, and B 0.84375. If it comes down to A and C then A will win with probability 0.109890, and C 0.890110.

• Pr(A**) = (0.560165975 × 0.15625) + (0.346473029 × 0.10989011) = 0.125600. A can be the winner two ways: (1) getting to the AB state, and then winning, or (2) getting to the AC state and then winning.
• Pr(B**) = 0.560166 × 0.84375 = 0.472640. B will be the winner if it gets to the AB state, and then B wins.
• Pr(C**) = 0.093361 + (0.346473 × 0.890110) = 0.401760. C can win by A killing B, and then C killing A in the first round, or by it getting to state AC, and then C winning.

So, if A’s strategy is to aim at B at first, then his probability of being the sole survivor is 12.56%.

Three Player — A Aims at C

If A hits C then B will definitely survive, and may or may not hit A. So two possible outcomes of hitting C are AB and B. If A misses C then B will aim at the greater threat C. If B hits C then A and B will survive. If B misses C then C will aim at the greater threat B. If C misses B then all three will survive. If C hits B then A and C will survive. So the possible outcomes are B, AB, AC, and ABC.

• Pr(A) = 0.
• Pr(B) = 0.1 × 0.6 = 0.06.
• Pr(C) = 0.
• Pr(AB) = (0.1 × 0.4) + (0.9 × 0.6) = 0.04+0.54 = 0.58. This can be achieved two ways. The first is A hitting C, and then B missing A. The second is A missing B, and then B hitting C.
• Pr(AC) = 0.9 × 0.4 × 0.9 = 0.324. This is achieved by A missing C, B missing C, and C hitting B.
• Pr(BC) = 0.
• Pr(ABC) = 0.9 × 0.4 × 0.1 = 0.036. This is achieved by all three missing.

By the same logic as the two-player cases, we can divide each outcome by (1-Pr(ABC))=0.964 to find the probabilities of each state, assuming that the state of the game did change after the round.

• Pr(B*) = 0.06/0.964 = 0.062241.
  
• Pr(AB*) = 0.58/0.964 = 0.601660.
  
• Pr(AC*) = 0.324/0.964 = 0.336100.

By the same logic as the solution for the A aims at B case:

• Pr(A**) = (0.601660 × 0.15625) + (0.336100 × 0.10989011) = 0.130943.
• Pr(B**) = 0.062241 + 0.601660 × 0.84375 = 0.569891.
• Pr(C**) = 0.336100 × 0.890110 = 0.299166.

So, if A’s strategy is to aim at C at first, then his probability of being the sole survivor is 13.09%.

Three Player — A Misses Deliberately

After A deliberately misses then B will aim at the greater threat C. If B hits C then A and B will survive. If B misses C then C will aim at the greater threat B. If C misses B then all three will survive. If C hits B then A and C will survive. So the possible outcomes are AB, AC, and ABC.

• Pr(A) = 0.
• Pr(B) = 0.
• Pr(C) = 0.
• Pr(AB) = 0.6. This is achieved by B hitting C.
• Pr(AC) = 0.4 × 0.9 = 0.36. This is achieved by B missing C, and then C hitting B.
• Pr(BC) = 0.
• Pr(ABC) = 0.4 × 0.1 = 0.04. This is achieved by all three missing.

By the same logic as the two-player cases, we can divide each outcome by (1-Pr(ABC))=0.96 to find the probabilities of each state, assuming that the state of the game did change after the round.

• Pr(AB*) = 0.6/0.96 = 0.625.
  
• Pr(AC*) = 0.36/0.96 = 0.375.

By the same logic as the solution for the A aims at B case:

• Pr(A**) = (0.625 × 0.15625) + (0.375 × 0.109890) = 0.138865.
• Pr(B**) = 0.625 × 0.84375 = 0.527344.
• Pr(C**) = 0.375 × 0.890110 = 0.333791.

So, if A’s strategy is to aim at C at first, then his probability of being the sole survivor is 13.89%.

This question was raised and discussed in the forum of my companion site Wizard of Vegas.