Ask The Wizard #171
Je ne pas compre your NIM game! I always thought the key to winning is to leave your opponent (in this case, the computer) with dots that add up to the next lowest number that equals its summary in binary numbers, that is, if I have 17 dots, I take 2 and leave 15, the summary of binary numbers 1,2,4,8. But this doesn’t seem to work. Am I right or wrong?
You are on the right track with the binary numbers but that is not quite the winning strategy. First, if you can leave your opponent with an odd number of rows of one each then do so. Otherwise break down each row into its binary components. For example, 99 would be 64+32+2+1. Then add up the number of each component over all the rows. Then look for a play that will leave your opponent with an even number of all binary components over all the rows.
Let’s look at an example. Suppose it is your turn with the following scenario.
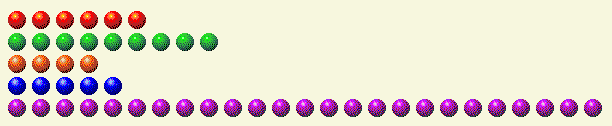
The following table breaks down each row into its binary components.
Player’s Turn 1
| Row | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 25 | 1 | 0 | 0 | 1 | 1 |
| Total | 3 | 1 | 3 | 2 | 1 |
You can see that there is an odd number of ones, twos, fours, and sixteens. Clearly we need to get the row of 25 under 16 to eliminate the 16 unit. To keep the total of the binary components even we need to remove the 1, add a 2, add a 4, keep the 8, and remove the 16. That means the best play is 2+4+8=14 in the last row. Leaving 14 in the bottom row we have the following.
Computer’s Turn 1
| Row | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| Total | 2 | 2 | 4 | 2 | 0 |
The computer takes its turn, leaving us with this.
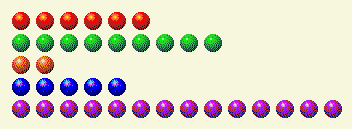
Here is the binary breakdown of that.
Player’s Turn 2
| Row | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 14 | 0 | 1 | 1 | 1 | 0 |
| Total | 2 | 3 | 3 | 2 | 0 |
Here we need to remove a 2 and a 4, to get those totals even. There is only one row, the 14, which has both components. So remove 6 from that, leaving 8.
Computer’s Turn 2
| Row | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| Total | 2 | 2 | 2 | 2 | 0 |
The computer takes its turn, leaving us with this.
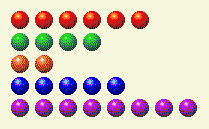
Now we need to change the 1, 4, and 8 columns.
Player’s Turn 3
| Row | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 0 |
| Total | 1 | 2 | 3 | 1 | 0 |
That can be done by changing the row of 8 to 5 as follows.
Computer’s Turn 3
| Row | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| Total | 2 | 2 | 4 | 0 | 0 |
The computer takes its turn, leaving us with this.
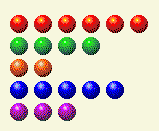
Now we need to change the 2 and 4 totals.
Player’s Turn 4
| Row | 1 | 2 | 4 | 8 | 16 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| Total | 2 | 3 | 3 | 0 | 0 |
This can be done by changing the 6 to a 0.
Computer’s Turn 4
| Row | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| Total | 2 | 2 | 2 | 0 | 0 |
The computer takes its turn, leaving us with this.
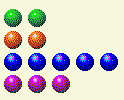
Now we need to change the 2s and 4s.
Player’s Turn 5
| Row | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| Total | 2 | 3 | 1 | 0 | 0 |
This can be accomplished by changing the row of 5 to 3. If you can ever get your opponent to an x,x,y,y situation you can’t help but win, if you can maintain the same situation until the end.
Computer’s Turn 5
| Row | 1 | 2 | 4 | 8 | 16 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 |
| Total | 2 | 4 | 0 | 0 | 0 |
The next few moves I keep the computer on x,x,y,y patterns. Here the computer leaves me with 2,2,3,2; so I leave it with 2,2,2,2.

The computer then gives me 2,2,1,2. I leave it with 2,2,1,1.
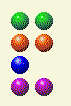
The computer then leaves me with 2,2,1. I leave it with 2,2. If you can ever get your opponent to two equal rows you can’t help but win, just keep the rows equal.

The computer then leaves me with a single pile of 2, and I remove 1.

Here is the end of the game.
I understand the put bet is a good bet when the odds are 10x or more. So, if the point is a 6 or 8, bet $5 plus $50 free odds for example. My question is, why wait for the point? Why not bet on the passline, and then if the point is a 6 or 8, bet the full 10x odds? This way you get the advantage of the odds, plus the advantage of the come out 7 / 11 roll. Am I missing something?
I agree. I don’t recommend making put or place bets, because as you said, the odds are better making a line bet and then maximum odds. However, some people absolutely must bet on the points directly. If that is a given, I advocate making the best bet between the place, buy, and put, which I explain in greater depth in my craps section.
My friend I were playing in LV. We had a big argument on what has statistically better odds, double down with player totaling 10 versus dealer showing 7, or double down with player totaling 11 versus dealer showing 10, in a two deck game. I thought it was the prior.
My blackjack appendix 9 was created for just these kinds of questions. Assuming 6 decks, my table shows the expected value of doubling 8+2 vs. 7 is 0.396342. The expected value of doubling 8+3 vs. 10 is 0.176919. So you are right, 10 vs. 7 is the much better hand to have.
Your site is awesome, I’ve learned so much from it. On the flop in holdem poker and you have 20 cards that give you the winning hand. Why is the percentage of you making your hand by the river 67.5% and not 86% (20/47 + 20/46)? I’ve looked everywhere and can’t seem to figure this out, even though I know it’s probably very elementary. I’d appreciate the help, Thanks!!
Thanks! Your way is double counting getting two of the 20 cards you need. The probability you get one of your 20 needed cards on the turn is 20/47 = 0.4255. The probability you don’t get it on the turn and then do get it on the river is (27/47)*(20/46) = 0.2498. So the total probability is 0.4255 + 0.2498 = 0.6753.
I recently witnessed a situation at the local tribal casino involving protocol at the craps table that puzzled me, and I'm wondering if you clarify it for me. On his come out roll, Player ’A’ threw a number and established a point. For the next roll, the player next to ’A’ (Player ’B’) picked up the dice and shot. It’s not clear why he did this, or if he even knew ’A’. One of the other players objected, pointing out that ’B’ was not the original shooter. After much discussion and head scratching by the dealers and the boxman, the dice were passed to the next player (Player ’C’) who finished the hand (he eventually sevened out).
Was this the correct protocol for this situation, and if so, what is the logic behind it? If Player ’A’ for some reason simply didn't want to shoot any more, why shouldn’t he be allowed to relinquish the dice? If Player ’B’ picked up the dice because he didn't understand the game, or if the stickman mistakenly put them in front of him, shouldn't the dice go back to ’A’ to finish the hand?
I asked the Bone Man at nextshooter.com this one. Here is what he said.
If a player other than the correct shooter picks up the dice and rolls them, it should be a no-call, no-roll and the dice should be returned to the correct shooter. Though this is indeed the proper ruling, the boxman in some instances may allow for the roll if the result is to the favor of all or most of the players. In some instances, the result of the roll may not effect any of the player(s) wagers. Also... Any player can request that the dice be sent to the next shooter to finish a hand. In such cases the same dice may be sent out or the new shooter can request new dice. Upon the completion of the roll, the SAME shooter can then shoot HIS/HER OWN HAND, thereby having more than one hand.
What is the chance of getting a sum over 100, when rolling 20 dice? Kind regards
I started to use the Normal approximation to solve this, but the probability of over 100 points is too low for that method to be accurate. So I did a random simulation of 8.25 million trials and the number of trails that were 101 points or more was 127. So the probability is about 1 in 65,000.
Time for another Deal or No Deal question. Let’s say after all the deals from the banker and guest appearances by Celine Dion, you’re left with two suitcases, the $500,000 and the $1,000,000. The banker’s offer will be slightly less than $750,000 I assume. Which would you choose? What if the two briefcase left were the $.01 and $1,000,000 one? I guess it’s all a matter if you’re a gambler or not, and nothing really to do with odds. The reason why I’m asking is I wonder if ANYBODY will ever win $1,000,000 (even if they’ve picked the magic briefcase).
When the prizes become life-changing amounts, the wise player should play conservatively at the expense of maximizing expected value. A good strategy should be to maximize expected happiness. A good function to measure happiness I think is the log of your total wealth. Let’s take a person with existing wealth of $100,000 who is presented with two cases of $0.01 and $1,000,000. By taking “no deal” the expected happiness is 0.5*log($100,000.01) + 0.5*log($1,100,000) = 5.520696. Let b be the bank offer where the player is indifferent to taking it.
log(b) = 5.520696
b = 105.520696
b = $331,662.50.
So this hypothetical player should be indifferent at a bank offer of $331,662.50. The lesser your wealth going into the game the more conservatively you should play. Usually in the late stages of the game the bank offers are close to expected value, sometimes a little more bit more. The only rational case where a player could win the million is if he had a lot of wealth going into the game and/or the bank offers were unusually stingy. The producers seem to like hard-working middle class people, so we’re unlikely to see somebody who can afford to be cavalier when large amounts are involved. I have also never seen the bank make offers under 90% of expected value late in the game. The time when we will see somebody win the million is when a degenerate gambler gets on the show who can’t stop. When that happens I will be rooting for the banker.
Love your site! I just ran across your detailed list of Las Vegas Blackjack tables and their edges, so I was wondering: Suppose that there two BJ tables, one with an edge of 0.2% with a table minimum of $10 and 0.4% with a table minimum of $5. Both tables have the same $0.02 loss per hand. Is there any advantage to choose one table over the other?
Thanks. To answer this question you first have to ask yourself why you are gambling in the first place. If you are trying to lose as little as possible then you shouldn’t play at all. However, if you are playing for the fun of gambling then I would choose the $10 game with the 0.2% edge. The expected loss will be the same but you’ll get more of a fix with the larger wagers.
There’s this Pai Gow Poker sidebet in Casino Niagara which pays out of a jackpot rather than at fixed odds. I’m wondering what amount the jackpot has to be at for that bet to break even (assuming one set the hand to maximize return of jackpot bet).
The break even point is $102,680.24. I just added an analysis of this bet to my section on Pai Gow Poker side bets.
I don't know a lot about poker, but I do find it fun, so maybe you can clear something up for me. On a recent trip to Vegas with my wife, we stayed at Arizona Charlie's Decatur. Our reason for staying here was because they had advertised $2-$4 Hold 'em on their website. On our first morning, we walk down to the poker room and put our names in for $2-$4. I notice the poker guy writing our names under the columns for $4-$8. So I told him we wanted $2-$4 (there was a column labeled “$2-$4” on the same sheet). He said it was $2-$4: $2 before the flop, $4 after the flop, and $8 after the turn and river. I described to him what I meant by $2-$4: $2 before and after the flop and $4 after the turn and river. He laughed at us like we didn’t know what we were talking about and said that’s not how the game is played. We ended up playing poker at the Gold Coast the remainder of our trip. Is this type of betting normal for poker rooms? (I ended up telling the poker room supervisor if we could afford $4-$8 Hold ‘em, we wouldn’t be staying at Arizona Charlie’s.)
I agree that a "2/4" game means the bets are in $2 units before the turn and $4 after the turn. However, the small blind is likely be $1. It sounds like when Arizona Charlie's is calling a game "2/4" they are referring to the blinds, which would mean a small blind of $2, and a big blind of $4, which would imply $8 bets after the turn. I've never heard this usage before so I don’t blame you for being surprised.
p.s. I later received the following from Anthony, a poker room supervisor.
I am a poker room supervisor. I was just writing to let you know about the correct wording for the poker limits in Texas Hold 'em. If as game is referred to as $2/4. It is referring to the bets. (A game is only referred to by the blinds if it is No-Limit.) $2 pre flop and post flop,$4 on the turn and the river.A game that is listed as $2/$4/$8 (which is exactly what I suspect the previous letter writer was actually referring to, is $2 pre-flop,$4 post-flop,$8 turn and river .It is also possible to have a game listed as $2/$4/$6/$8. Just passing the information on, good poker supervisors want people to have as much information as possible.




