Per the casino's own rules, the jackpot is not triggered by the cards but an internal mechanism. Here is a screenshot of how they explain it:
Strategy
Unfortunately, there is no easy way to quantify strategy for this game that I'm aware of. The good news is that most of the time the right play is pretty obvious. For those cases that aren't, you can find the best play by adding the expected value of all options for each hand. The following three tables show the expected value of each player hand by dealer up card for standing, hitting and doubling respectively.
Expected Values for Standing Expand
| Hard |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Ace |
| 4 |
-0.2930 |
-0.2516 |
-0.2084 |
-0.1632 |
-0.1543 |
-0.4761 |
-0.5126 |
-0.5415 |
-0.5751 |
-0.7691 |
| 5 |
-0.2930 |
-0.2516 |
-0.2084 |
-0.1632 |
-0.1543 |
-0.4761 |
-0.5126 |
-0.5415 |
-0.5751 |
-0.7691 |
| 6 |
-0.2930 |
-0.2516 |
-0.2084 |
-0.1632 |
-0.1543 |
-0.4761 |
-0.5126 |
-0.5415 |
-0.5751 |
-0.7691 |
| 7 |
-0.2930 |
-0.2516 |
-0.2084 |
-0.1632 |
-0.1543 |
-0.4761 |
-0.5126 |
-0.5415 |
-0.5751 |
-0.7691 |
| 8 |
-0.2930 |
-0.2516 |
-0.2084 |
-0.1632 |
-0.1543 |
-0.4761 |
-0.5126 |
-0.5415 |
-0.5751 |
-0.7691 |
| 9 |
-0.2930 |
-0.2516 |
-0.2084 |
-0.1632 |
-0.1543 |
-0.4761 |
-0.5126 |
-0.5415 |
-0.5751 |
-0.7691 |
| 10 |
-0.2930 |
-0.2516 |
-0.2084 |
-0.1632 |
-0.1543 |
-0.4761 |
-0.5126 |
-0.5415 |
-0.5751 |
-0.7691 |
| 11 |
-0.2930 |
-0.2516 |
-0.2084 |
-0.1632 |
-0.1543 |
-0.4761 |
-0.5126 |
-0.5415 |
-0.5751 |
-0.7691 |
| 12 |
-0.2930 |
-0.2516 |
-0.2084 |
-0.1632 |
-0.1543 |
-0.4761 |
-0.5126 |
-0.5415 |
-0.5751 |
-0.7691 |
| 13 |
-0.2930 |
-0.2516 |
-0.2084 |
-0.1632 |
-0.1543 |
-0.4761 |
-0.5126 |
-0.5415 |
-0.5751 |
-0.7691 |
| 14 |
-0.2930 |
-0.2516 |
-0.2084 |
-0.1632 |
-0.1543 |
-0.4761 |
-0.5126 |
-0.5415 |
-0.5751 |
-0.7691 |
| 15 |
-0.2930 |
-0.2516 |
-0.2084 |
-0.1632 |
-0.1543 |
-0.4761 |
-0.5126 |
-0.5415 |
-0.5751 |
-0.7691 |
| 16 |
-0.2930 |
-0.2516 |
-0.2084 |
-0.1632 |
-0.1543 |
-0.4761 |
-0.5126 |
-0.5415 |
-0.5751 |
-0.7691 |
| 17 |
-0.1533 |
-0.1173 |
-0.0778 |
-0.0413 |
0.0114 |
-0.1069 |
-0.3837 |
-0.4212 |
-0.4631 |
-0.6390 |
| 18 |
0.1207 |
0.1475 |
0.1768 |
0.2029 |
0.2833 |
0.4002 |
0.1052 |
-0.1835 |
-0.2396 |
-0.3782 |
| 19 |
0.3851 |
0.4033 |
0.4221 |
0.4429 |
0.4959 |
0.6166 |
0.5939 |
0.2857 |
-0.0159 |
-0.1168 |
| 20 |
0.6392 |
0.6493 |
0.6598 |
0.6723 |
0.7039 |
0.7737 |
0.7918 |
0.7579 |
0.4360 |
0.1447 |
| 21 |
0.8816 |
0.8851 |
0.8881 |
0.8921 |
0.9027 |
0.9262 |
0.9305 |
0.9391 |
0.8108 |
0.3291 |
| BJ |
2.0000 |
2.0000 |
2.0000 |
2.0000 |
2.0000 |
2.0000 |
2.0000 |
2.0000 |
2.0000 |
2.0000 |
| 12 |
-0.2930 |
-0.2516 |
-0.2084 |
-0.1632 |
-0.1543 |
-0.4761 |
-0.5126 |
-0.5415 |
-0.5751 |
-0.7691 |
| 13 |
-0.2930 |
-0.2516 |
-0.2084 |
-0.1632 |
-0.1543 |
-0.4761 |
-0.5126 |
-0.5415 |
-0.5751 |
-0.7691 |
| 14 |
-0.2930 |
-0.2516 |
-0.2084 |
-0.1632 |
-0.1543 |
-0.4761 |
-0.5126 |
-0.5415 |
-0.5751 |
-0.7691 |
| 15 |
-0.2930 |
-0.2516 |
-0.2084 |
-0.1632 |
-0.1543 |
-0.4761 |
-0.5126 |
-0.5415 |
-0.5751 |
-0.7691 |
| 16 |
-0.2930 |
-0.2516 |
-0.2084 |
-0.1632 |
-0.1543 |
-0.4761 |
-0.5126 |
-0.5415 |
-0.5751 |
-0.7691 |
| 17 |
-0.1533 |
-0.1173 |
-0.0778 |
-0.0413 |
0.0114 |
-0.1069 |
-0.3837 |
-0.4212 |
-0.4631 |
-0.6390 |
| 18 |
0.1207 |
0.1475 |
0.1768 |
0.2029 |
0.2833 |
0.4002 |
0.1052 |
-0.1835 |
-0.2396 |
-0.3782 |
| 19 |
0.3851 |
0.4033 |
0.4221 |
0.4429 |
0.4959 |
0.6166 |
0.5939 |
0.2857 |
-0.0159 |
-0.1168 |
| 20 |
0.6392 |
0.6493 |
0.6598 |
0.6723 |
0.7039 |
0.7737 |
0.7918 |
0.7579 |
0.4360 |
0.1447 |
| 21 |
0.8816 |
0.8851 |
0.8881 |
0.8921 |
0.9027 |
0.9262 |
0.9305 |
0.9391 |
0.8108 |
0.3291 |
Expected Values for Hitting Expand
| Hard |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Ace |
| 4 |
-0.1153 |
-0.0824 |
-0.0474 |
-0.0087 |
0.0106 |
-0.0881 |
-0.1596 |
-0.2408 |
-0.3431 |
-0.4362 |
| 5 |
-0.1286 |
-0.0951 |
-0.0594 |
-0.0203 |
-0.0017 |
-0.1192 |
-0.1884 |
-0.2667 |
-0.3655 |
-0.4362 |
| 6 |
-0.1411 |
-0.1070 |
-0.0708 |
-0.0312 |
-0.0135 |
-0.1517 |
-0.2175 |
-0.2927 |
-0.3880 |
-0.4362 |
| 7 |
-0.1096 |
-0.0765 |
-0.0409 |
-0.0037 |
0.0288 |
-0.0687 |
-0.2113 |
-0.2849 |
-0.3705 |
-0.4362 |
| 8 |
-0.0224 |
0.0078 |
0.0404 |
0.0744 |
0.1146 |
0.0826 |
-0.0604 |
-0.2104 |
-0.3059 |
-0.4362 |
| 9 |
0.0738 |
0.1010 |
0.1299 |
0.1615 |
0.1957 |
0.1722 |
0.0981 |
-0.0527 |
-0.2167 |
-0.4362 |
| 10 |
0.1819 |
0.2058 |
0.2313 |
0.2592 |
0.2875 |
0.2572 |
0.1977 |
0.1163 |
-0.0526 |
-0.4362 |
| 11 |
0.2379 |
0.2602 |
0.2840 |
0.3099 |
0.3334 |
0.2924 |
0.2297 |
0.1581 |
0.0339 |
-0.2097 |
| 12 |
-0.2537 |
-0.2337 |
-0.2127 |
-0.1911 |
-0.1708 |
-0.2127 |
-0.2718 |
-0.3401 |
-0.4280 |
-0.5510 |
| 13 |
-0.3081 |
-0.2913 |
-0.2735 |
-0.2554 |
-0.2358 |
-0.2689 |
-0.3238 |
-0.3872 |
-0.4689 |
-0.5831 |
| 14 |
-0.3625 |
-0.3489 |
-0.3344 |
-0.3198 |
-0.3009 |
-0.3211 |
-0.3721 |
-0.4310 |
-0.5068 |
-0.6128 |
| 15 |
-0.4169 |
-0.4064 |
-0.3953 |
-0.3842 |
-0.3659 |
-0.3696 |
-0.4170 |
-0.4717 |
-0.5420 |
-0.6405 |
| 16 |
-0.4713 |
-0.4640 |
-0.4562 |
-0.4485 |
-0.4310 |
-0.4146 |
-0.4586 |
-0.5094 |
-0.5748 |
-0.6662 |
| 17 |
-0.5364 |
-0.5319 |
-0.5272 |
-0.5223 |
-0.5088 |
-0.4833 |
-0.5060 |
-0.5539 |
-0.6161 |
-0.6939 |
| 18 |
-0.6226 |
-0.6202 |
-0.6177 |
-0.6148 |
-0.6075 |
-0.5910 |
-0.5911 |
-0.6167 |
-0.6745 |
-0.7418 |
| 19 |
-0.7292 |
-0.7281 |
-0.7271 |
-0.7258 |
-0.7226 |
-0.7154 |
-0.7137 |
-0.7156 |
-0.7502 |
-0.8097 |
| 20 |
-0.8553 |
-0.8550 |
-0.8548 |
-0.8545 |
-0.8536 |
-0.8518 |
-0.8515 |
-0.8508 |
-0.8607 |
-0.8978 |
| 21 |
-1.0000 |
-1.0000 |
-1.0000 |
-1.0000 |
-1.0000 |
-1.0000 |
-1.0000 |
-1.0000 |
-1.0000 |
-1.0000 |
| Soft |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Ace |
| 12 |
0.0813 |
0.1033 |
0.1279 |
0.1597 |
0.1856 |
0.1658 |
0.0949 |
-0.0002 |
-0.1407 |
-0.3228 |
| 13 |
0.0461 |
0.0741 |
0.1038 |
0.1366 |
0.1613 |
0.1227 |
0.0538 |
-0.0380 |
-0.1729 |
-0.3482 |
| 14 |
0.0219 |
0.0508 |
0.0815 |
0.1152 |
0.1388 |
0.0798 |
0.0130 |
-0.0754 |
-0.2049 |
-0.3735 |
| 15 |
-0.0006 |
0.0292 |
0.0608 |
0.0953 |
0.1178 |
0.0373 |
-0.0273 |
-0.1124 |
-0.2365 |
-0.3985 |
| 16 |
-0.0215 |
0.0092 |
0.0416 |
0.0769 |
0.0984 |
-0.0046 |
-0.0670 |
-0.1489 |
-0.2677 |
-0.4231 |
| 17 |
-0.0010 |
0.0289 |
0.0610 |
0.0945 |
0.1277 |
0.0540 |
-0.0736 |
-0.1494 |
-0.2577 |
-0.4327 |
| 18 |
0.0623 |
0.0900 |
0.1198 |
0.1509 |
0.1904 |
0.1710 |
0.0392 |
-0.1009 |
-0.2085 |
-0.3729 |
| 19 |
0.1233 |
0.1490 |
0.1764 |
0.2063 |
0.2395 |
0.2210 |
0.1520 |
0.0073 |
-0.1569 |
-0.3126 |
| 20 |
0.1819 |
0.2058 |
0.2313 |
0.2592 |
0.2875 |
0.2572 |
0.1977 |
0.1163 |
-0.0526 |
-0.2523 |
| 21 |
0.2379 |
0.2602 |
0.2840 |
0.3099 |
0.3334 |
0.2924 |
0.2297 |
0.1581 |
0.0339 |
-0.2097 |
Expected Values for DoublingExpand
| Hard |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Ace |
| 4 |
-0.5860 |
-0.5032 |
-0.4168 |
-0.3264 |
-0.3086 |
-0.9523 |
-1.0252 |
-1.0830 |
-1.1501 |
-1.5381 |
| 5 |
-0.5860 |
-0.5032 |
-0.4168 |
-0.3264 |
-0.3086 |
-0.9523 |
-1.0252 |
-1.0830 |
-1.1501 |
-1.5381 |
| 6 |
-0.5645 |
-0.4826 |
-0.3967 |
-0.3076 |
-0.2831 |
-0.8955 |
-1.0054 |
-1.0645 |
-1.1329 |
-1.5181 |
| 7 |
-0.4364 |
-0.3592 |
-0.2772 |
-0.1951 |
-0.1393 |
-0.5902 |
-0.8508 |
-0.9539 |
-1.0296 |
-1.3980 |
| 8 |
-0.2056 |
-0.1362 |
-0.0627 |
0.0109 |
0.0862 |
-0.1881 |
-0.4550 |
-0.7170 |
-0.8404 |
-1.1772 |
| 9 |
0.0599 |
0.1205 |
0.1841 |
0.2502 |
0.3164 |
0.1041 |
-0.0287 |
-0.3005 |
-0.5817 |
-0.9160 |
| 10 |
0.3578 |
0.4089 |
0.4625 |
0.5184 |
0.5750 |
0.3923 |
0.2847 |
0.1452 |
-0.1599 |
-0.6264 |
| 11 |
0.4697 |
0.5177 |
0.5679 |
0.6199 |
0.6667 |
0.4627 |
0.3487 |
0.2289 |
0.0131 |
-0.5412 |
| 12 |
-0.5075 |
-0.4675 |
-0.4253 |
-0.3821 |
-0.3415 |
-0.5069 |
-0.6173 |
-0.7366 |
-0.8880 |
-1.1902 |
| 13 |
-0.6163 |
-0.5826 |
-0.5471 |
-0.5109 |
-0.4717 |
-0.5875 |
-0.6923 |
-0.8072 |
-0.9534 |
-1.2257 |
| 14 |
-0.7250 |
-0.6977 |
-0.6689 |
-0.6396 |
-0.6018 |
-0.6681 |
-0.7673 |
-0.8777 |
-1.0188 |
-1.2613 |
| 15 |
-0.8338 |
-0.8129 |
-0.7907 |
-0.7684 |
-0.7319 |
-0.7487 |
-0.8423 |
-0.9482 |
-1.0841 |
-1.2968 |
| 16 |
-0.9426 |
-0.9280 |
-0.9125 |
-0.8971 |
-0.8620 |
-0.8293 |
-0.9173 |
-1.0188 |
-1.1495 |
-1.3323 |
| 17 |
-1.0728 |
-1.0638 |
-1.0543 |
-1.0446 |
-1.0176 |
-0.9667 |
-1.0121 |
-1.1078 |
-1.2321 |
-1.3879 |
| 18 |
-1.2453 |
-1.2404 |
-1.2354 |
-1.2296 |
-1.2150 |
-1.1821 |
-1.1821 |
-1.2334 |
-1.3491 |
-1.4835 |
| 19 |
-1.4583 |
-1.4562 |
-1.4542 |
-1.4516 |
-1.4451 |
-1.4308 |
-1.4273 |
-1.4312 |
-1.5005 |
-1.6194 |
| 20 |
-1.7105 |
-1.7100 |
-1.7095 |
-1.7089 |
-1.7073 |
-1.7037 |
-1.7030 |
-1.7017 |
-1.7214 |
-1.7955 |
| 21 |
-2.0000 |
-2.0000 |
-2.0000 |
-2.0000 |
-2.0000 |
-2.0000 |
-2.0000 |
-2.0000 |
-2.0000 |
-2.0000 |
| Soft |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Ace |
| 12 |
-0.0724 |
-0.0069 |
0.0618 |
0.1328 |
0.1789 |
-0.1845 |
-0.3174 |
-0.4545 |
-0.6265 |
-1.0481 |
| 13 |
-0.0724 |
-0.0069 |
0.0618 |
0.1328 |
0.1789 |
-0.1845 |
-0.3174 |
-0.4545 |
-0.6265 |
-1.0481 |
| 14 |
-0.0724 |
-0.0069 |
0.0618 |
0.1328 |
0.1789 |
-0.1845 |
-0.3174 |
-0.4545 |
-0.6265 |
-1.0481 |
| 15 |
-0.0724 |
-0.0069 |
0.0618 |
0.1328 |
0.1789 |
-0.1845 |
-0.3174 |
-0.4545 |
-0.6265 |
-1.0481 |
| 16 |
-0.0724 |
-0.0069 |
0.0618 |
0.1328 |
0.1789 |
-0.1845 |
-0.3174 |
-0.4545 |
-0.6265 |
-1.0481 |
| 17 |
-0.0080 |
0.0551 |
0.1221 |
0.1891 |
0.2554 |
-0.0141 |
-0.2579 |
-0.3990 |
-0.5749 |
-0.9881 |
| 18 |
0.1185 |
0.1773 |
0.2396 |
0.3018 |
0.3808 |
0.2200 |
-0.0322 |
-0.2893 |
-0.4717 |
-0.8677 |
| 19 |
0.2406 |
0.2953 |
0.3528 |
0.4126 |
0.4790 |
0.3198 |
0.1933 |
-0.0727 |
-0.3685 |
-0.7470 |
| 20 |
0.3578 |
0.4089 |
0.4625 |
0.5184 |
0.5750 |
0.3923 |
0.2847 |
0.1452 |
-0.1599 |
-0.6264 |
| 21 |
0.4697 |
0.5177 |
0.5679 |
0.6199 |
0.6667 |
0.4627 |
0.3487 |
0.2289 |
0.0131 |
-0.5412 |

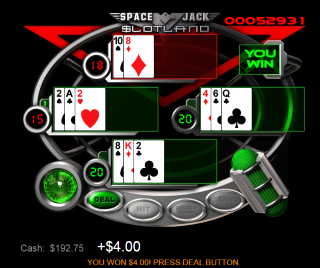
Example
Let's look at the hand pictured on the right as an example. Doubling is clearly an awful decision, so we can narrow down the viable options to hitting and standing. Basic strategy says to hit 12 against 2 and stand 19 against 2. While hitting is right on two out of three hands, it is only marginally right on the two 12s. Meanwhile, standing is by far the right play for the 19. However, enough talk, let's do the math and calculate the expected value (EV) for hitting and standing:
EV of standing = 2×-0.2930 + 0.3851 = -0.2003
EV of hitting = 2×-0.2537 - 0.7292 = -1.2366
So, you can expect to lose -0.2003 hands by standing and -1.2366 by hitting. It isn't even close; standing is the better play.
Action Frequencies
Here is how often each action is taken on the initial two card hands:
- Stand: 64.15%
- Hit: 34.11%
- Double: 1.73%
- Jackpot (assuming fair game): 0.0089%.
Analysis
Before considering the jackpot, the house advantage in Space Jack is 6.61% of all initial wagers. For example, if the player makes three bets of $10, then he can expected to lose $10 × 3 × 6.61% = $1.98.
If the cards were dealt fairly for jackpot purposes, then the probability of winning the jackpot with three blackjacks would be 1 in 11,206. Based on a $15 total bet, the value for each $10,000 in the jackpot would be 5.95%. The meter would need to be only $11,117 to reach breakeven. At the minimum jackpot of $50,000 and $15 bet, the player advantage would be 23.13%. At a $100,000 jackpot, it would be 52.88%.
However, all that is moot because they admit the jackpot is not determined by the random draw of the cards but rather generated randomly, behind the scenes. Nowhere is it disclosed what this probability is.
Given that the odds of the jackpot are not quantifiable, I would ignore that element to the game and assume a house edge of 6.61%, which is quite high for a table game. Keep in mind the house edge in conventional blackjack is about 0.5%, depending on the specific rules. Draw your own conclusion.
Blacklist
I am big on open and honest gambling. Part of that means electronic representations of physical gambling equipment like cards, dice and balls conform to natural probabilities, as if played in real life. By their own admission, Slotland does not trigger the jackpot in card games by the cards themselves. For this reason, Slotland was on my online casino blacklist for years.
However, in late 2022 we did a fresh review of Slotland and saw they removed the game. In the interests of fairness and redemption, we removed them from the blacklist.