Probability - Cards
I was playing baccarat online and out of 75 hands the banker won 52 and the player 23. This is a difference of 29, what is the probability of that happening?
First, I'm going to assume that you are not counting ties. In other words, you mean 75 bets resolved. It would be very unlikely to go 75 hands without a tie. The expected number of banker wins out of 75 bets resolved is 38.00913745. The standard deviation is the square root of the product of 75, the probability of a banker win, and the probability of a player win. The probability of a banker win, given that there wasn't a tie, is 0.506788499 and the probability of a player win is 0.493211501 . The standard deviation is thus 4.329727904 . Then you'll have to make a half point correction for a binomial distribution and look up the Z statistic in a standard normal table (this step is left to the reader). The final answer is that the probability of the banker getting 52 or more wins is .0009. Your question also allowed for the possibility of the banker winning 23 or fewer times (also a difference of 29 more more) which has a probability of .0004 . So the final answer is that the probability of a difference of 29 or more is .0013, or 1 in 769.
When I calculate the combos of player and dealer hands for Caribbean Stud Poker, I get only 3,986,646,103,440 vs your 19, etc. I'm off by exactly a factor of 5. I used combin(52,5)*combin(47,5). Where did I go wrong? Thanks and I think your site is just great.
Thanks for the compliment. You are off by a factor of five because the dealer can have any one of 5 cards face up. In other words order does matter with the dealer's hand, since the first card is dealt face up. The correct derivation of the total combinations is combin(52,5)*47*combin(46,4) = 19,933,230,517,200.
What are the odds in drawing three cards to a pair and getting a full house at five-card draw poker?
There are two ways to get a full house in this situation: (1) draw a three of a kind or (2) draw one more to the pair and another pair. I'm going to assume you discard three singletons.
First, lets work out the number of combinations under (1). There are 3 ranks with only 3 suits left (remember you discarded 3 singletons) and 9 ranks with 4 suits left. The number of combinations is thus 3*combin(3,3)+9*combin(4,3) = 3*1 + 9*4 = 39.
Next, let's work out the number of combinations under (2). There are 2 suits left to add to the existing pair. There are combin(3,2) ways to form a pair from the 3 ranks with 3 cards left and combin(4,2) ways to form a pair to from the ranks with 4 cards left. So the total combinations under 2 is 2*(3*combin(3,2)+9*combin(4,2)) = 2*(3*3 + 9*6) = 126. The total number of ways to arrange a full house is the sum under (1) and (2), or 39+126=165. There are combin(47,3)=16,215 ways to arrange the 3 cards on the second draw. The probability of drawing a full house is the number of ways to draw a full house divided by the total combinations, or 165/16,215 = 0.0101758, or about 1 in 98.
For more information on the combin() function, please see my section on probabilities in poker page.
I started playing poker with my friends once a week (five-card draw, stud, seven-card stud). We have seven players at the table. It seems to me the probability of getting the hands would be reduced dramatically due to the numbers of players being allocated cards from a 52 card deck. Do you have a mathematical formula that could direct me in the proper direction?
No, the probability of getting any given hand is the same regardless of how many other players are at the table. An unseen card is an unseen card, it doesn't matter if another player has it or it is still in the deck.
I was recently told a story that I could not believe!! A friend of mine told me that at a friendly poker game at his house, he and his friend both pulled a natural straight flush in the same hand without drawing any cards!! (in five card draw) I find this hard to believe and from your site I computed the odds of one straight flush to be approx 65,000 to one, what would the odds of 2 in one hand be with 6 players in the game (without drawing any cards??)
I'm going to give an approximate answer by assuming that each player was dealt a hand from a separate deck. This should not change the odds much. The probability of any one player drawing a straight flush as found in my section on probabilities in poker is 36/2,598,960. Lets call this probability p. The probability of two players drawing a straight flush is combin(6,2)*p2*(1-p)4 = .0000000028779. In other words, the odds against this happening are 347,477,740 to 1.
How do you go about working out the separate probabilities for getting: (1) queen high, (2) king high, and (3) ace high in three card poker?
I'll just work out the king high first and briefly show the formula for the other two. The probability will be the number of king high hands divided by the total number of hands. The number of ranks less than king is 11. The king high hand must have two different of these ranks. The number of ways to arrange 2 out of 11 is combin(11,2) = 55. However, one of these combinations is king-queen-jack, resulting in a straight, so subtracting that combination there are 54 left that do not form a straight. Next, there are four suits for each rank, or 43=64 possible combinations of suits. However, four of these 64 result in a flush so there are 64-4=60 combinations of suits left. So, the total number of king high combinations is 54*60=3240. There are a total of combin(52,3)=22,100 to arrange 3 cards out of 52. So, the probability of forming a king high is 3,240/22,100 = 0.1466063 . The probability for ace high is: (combin(12,2)-2)*(43-4)/combin(52,3)=0.1737557. Note the -2 instead of -1 because of both the a-2-3 and q-k-a straights.
The probability for queen high is: (combin(10,2)-1)*(43-4)/combin(52,3)=0.119457.
What are the odds of being dealt a Royal Flush? Of being dealt a SEQUENTIAL Royal Flush (forwards or backwards)?
The probability of any royal flush is the number of possible royals, which is four (one for each suit), divided by the number of ways to choose 5 cards out of 52, which is combin(52,5)=2,598,960. So, the answer is 4/2,598,960 = 0.00000153908, or 1 in 649,740.
The probability of a sequential royal flush equals (number of suits) * (number of directions) / (total permutations of 5 cards out of 52) = 4 * 2 / permut(52,5) = 8 / 311,875,200 = 8 /
number of possible royals, which is four (one for each suit), times the number of directions it can be in divided by the number of ways to pick 5 cards out of 52, which is permut(52,5)=311,875,200. So, the answer is 4/311,875,200 = 0.00000002565, or 1 in 38,984,400 .
I like to play the game liars poker with dollar bills. what is the probability of getting any 1,2,3,4, or 5 of the same number on a bill. thank you. If I am playing with 3 people, what is the probability of any 1 number showing up.
First let me answer the unasked question on the probability that a specific number will show up n times on a random bill. There are 8 digits on a bill so the probability of n of a specific number is combin(8,n)*0.1n*0.98-n/108. Here is a table showing the probability for 0 to 8 of a specific number.
Specific Number Oddsin Liar's Poker
| Number | Probability |
|---|---|
| 8 | 0.00000001 |
| 7 | 0.00000072 |
| 6 | 0.00002268 |
| 5 | 0.00040824 |
| 4 | 0.00459270 |
| 3 | 0.03306744 |
| 2 | 0.14880348 |
| 1 | 0.38263752 |
| 0 | 0.43046721 |
| Total | 1.00000000 |
The next table shows the probability of every possible type of bill, categorized by the number of each n-of-a-kind. For example, the serial number 66847680 would have one three of a kind, one pair, and three singletons, for a probability of 0.1693440.
General Probabilities in Liar's Poker
| 8 o.a.k. | 7 o.a.k. | 6 o.a.k. | 5 o.a.k. | 4 o.a.k. | 3 o.a.k. | 2 o.a.k. | 1 o.a.k. | Probability |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.0000001 | |||||||
| 1 | 1 | 0.0000072 | ||||||
| 1 | 1 | 0.0000252 | ||||||
| 1 | 2 | 0.0002016 | ||||||
| 1 | 1 | 0.0000504 | ||||||
| 1 | 1 | 1 | 0.0012096 | |||||
| 1 | 3 | 0.0028224 | ||||||
| 2 | 0.0000315 | |||||||
| 1 | 1 | 1 | 0.0020160 | |||||
| 1 | 2 | 0.0015120 | ||||||
| 1 | 1 | 2 | 0.0211680 | |||||
| 1 | 4 | 0.0211680 | ||||||
| 2 | 1 | 0.0020160 | ||||||
| 2 | 2 | 0.0141120 | ||||||
| 1 | 2 | 1 | 0.0423360 | |||||
| 1 | 1 | 3 | 0.1693440 | |||||
| 1 | 5 | 0.0846720 | ||||||
| 4 | 0.0052920 | |||||||
| 3 | 2 | 0.1270080 | ||||||
| 2 | 4 | 0.3175200 | ||||||
| 1 | 6 | 0.1693440 | ||||||
| 8 | 0.0181440 | |||||||
| Total | 1.0000000 | |||||||
o.a.k. = "of a kind"
For more information, see my page on liars poker.
With a 52-card deck, what are the odds of drawing a pair of Jacks?
Assuming you draw five cards, and count all hands with exactly two jacks, then the probability would be combin(4,2)*combin(48,3)/combin(52,5) = 6*17296/2598960 = 3.99%.
What is the probability of getting a three pair in Pai Gow Poker? Are the chances lesser or greater than three of a kind?
Not counting a three of a kind and two pairs, the following are the ways to get a three pair and number of combinations.
No wild card: combin(13,3)*10*63*4 =2471040
Wild card used to compete pair of aces: combin(12,2)*10*62*42 = 380,160
Wild card used as singleton ace: combin(12,3)*63 = 47,520
The total number of combinations is 2,898,720. This is less than half of the 747,0676 combinations for a three of a kind.
The odds according to your formula for a royal flush is 4/2,598,960 = 1/649,740. So, if I was playing Caribbean Stud one-on-one with the dealer, then my hand and the dealers would equal 649,740*2=1,299,480. Therefore, according to the math, after 1,299,480 hands there should be two royal flushes. Please tell me if I understand the odds correctly.
You, are right that on average a royal flush will occur once in every 649,740 hands, and that in 1,299,480 hands the expected number of royal flushes is 2. However, this is only the average. With every hand that goes by you are no closer to getting a royal. Every game of independent trials has this memory-less property so a royal flush is never overdue.
The probability of zero royals in 1,299,480 hands is 13.53%.
Hi, I am regular player of Pai Gow Poker, and I noticed your site has a lot of great information on the game. The other day when I was playing with a friend of mine he was dealt a 9-high hand, which I believe is the lowest hand possible. In all the time I had spent playing the game I had only seem it happen once before. Then five hands later he got the exact same hand(2-3-4-5-7-8-9). We couldn't believe it and were wondering what the odds of that happening were so we thought we would ask you. Thanks for your time and your great site.
There are two ways to arrange the ranks for form a 9 high hand, the one you mentioned and 2-3-4-6-7-8-9. The number of suit combinations without forming a flush is 47-4*(combin(7,5)*3^2+6*3+1) = 15,552. So the probability of a 9 high hand is 2*15,552/combin(53,7) = 31,104/154,143,080, or 1 in 9,911. If you were to play just five times the probability of getting 2 9-high hands would be 1 in 9,826,685. That this happened is a coincidence I believe as opposed to a fault in the random number generator or the coding of the program.
My question has to do with the House edge and element of risk calculations for Casino War for the Casino Niagara Rules (i.e., 3-1 pay out on raise and lose the original wager). How did you come up with these numbers I am currently trying to calculate them? I am having trouble. Thanks for you help.
Let's let d be the number of decks. The probability of a tie on the first round is (4*d-1)/(52*d-1)= 0.073955. The probability of a tie in the second round is 12*4*d/(52*d-2)*(4*d-1)/(52*d-3)+(4*d-2)/(52*d-2)*(4*d-3)/(52*d-3) = 0.073974. Lets call p1 the probability of a tie in the first round and p2 the probability of a tie in the second round. Then the player return is p1*(2*p2 +(1-p2)/2*(1-2))= -0.023301. Multiply by -1 and you have the house edge of 2.33%. I hope I didn't go over this too quickly.
Could you tell me how the total number of combinations in Caribbean, 19,933,230,517,200 are arrived at? I followed your 5-card poker combinations to get the 2,598,960. From there how do I continue? Thank you in advance.
You correctly calculated the number of player combinations as combin(52,5)=2,598,960. From there, the dealer can have combin(47,5)=1,533,939 possible hands. Then any one of five dealer cards can be face up. So 2,598,960*1,533,959*5=19,933,230,517,200.
First let me say, I think your web site is really great. I have told a few people about it, and hope they will try it too. I wish you continued success with it. I also liked the link to WinPoker. I liked WinPoker enough to order it. This is a great program. I have a question that I am hoping you can help me with. I have been trying to figure out the number of times each hand in seven-card stud occurs. I have a copy of your seven-card table, but I am interested in the mathematics to arrive at those numbers. I can figure out the five-card numbers, but the seven-card just baffles me. I would like to send an Excel 2000 file with my numbers. I would also like to know how to figure the number of straights in a 53-card deck with a joker. H E L P ! ! !
Thanks for your kind words. I agree that calculating the numbers for seven-card stud is hard. That is why I do it my computer. My program goes through all possible combinations and scores each one. The number of wild straights in pai gow poker is 11*(44-4)+10*3*(44-4)=10332. Combined with the 10200 natural straights the total is 20532.
I understand what the odds of being dealt a royal, straight flush are for any individual on a Caribbean Stud Poker or Let it Ride table are and how they are derived. But my question is this: as a 3rd party watching the game what are the odds of seeing any one of these hands being dealt to a player at the table on any given deal. I must believe it is dependant on the number of hands in play...is it merely the individual’s odds times the number of hands in play. ie. seeing a royal dealt on any particular hand with 4 players on a table means 4*odds of getting a royal? I’m slightly perplexed!
Your method is a good approximation. However by that logic, when flipping a coin, the probability of at least one person in 3 flipping a heads would be 3*50%=150%. Assuming independent events the probability of at least one success out of n trials, where the probability of each success is p, is 1-(1-p)n. In the case of the coin flipping example this would be 1-.53=0.875. In the case of four players of Caribbean Stud Poker the probability of at least one royal flush would be 1-(1-4/2598960)4 = 0.00000615629. However since all the cards are dealt out of the same deck the events are not independent. The math gets very complicated to determine the exact right answer and the approximation should be very close to the right answer.
What is the probability of being dealt a natural seven card straight flush in pai gow poker? I work in a casino and just saw this for the first time in 15 years. The lucky patron won $40,000.
There are 32 possible natural straight flushes (4 ranks times 8 possible spans of 7 cards). There are combin(53,7) = 154143080 possible ways 7 cards can be drawn out of 53. So the answer is 32/154143080, or 1 in 4816971.
What is the probability of getting two identical straight flushes (in both ranks and suit) two hands in a row in Three Card Poker?
The probability of getting a straight flush on the first hand is 4*12/combin(52,3) = 48/22100 =~ 0.0022. The probability that the next hand will be exactly the same is 1/22100. So the answer is (48/22100)*(1/22100) = 48/488410000, on 1 in 10,175,208. This is a 1.37 more likely than hitting a 6/49 lottery, which has a probability of 1 in 13983816.
In an 8 deck baccarat, what is the probability of getting an Ace and an 8 of Diamonds for both the player and the banker in a same deal?
(82/combin(416,2))* (72/combin(414,2)) = 0.00000043, or 1 in 2308093
I recently witnessed a strange event. I was watching five card draw poker, where you could only draw a maximum of 2 cards. One player drew 1 card and completed a heart flush. The dealer drew one card, and drew a spade flush. Naturally, the dealer’s flush was higher. There were 3 other players in the game. What are the odds of having two flushes in the same hand?
Let’s define the probability of a flush of either getting one on the deal, or drawing to a 4-card flush. For the sake of simplicity we’ll assume a player will draw to a pat pair or straight with 4 to a flush. The probability of getting a flush on the deal (not including a straight/royal flush) is 4*(combin(13,5)-10)/combin(52,5) = 5108/2598960 = 0.0019654. The probability of being dealt a 4-card flush is 4*3*combin(13,4)*13/combin(52,5) = 111540/2598960 = 0.0429172. The probability of completing the flush on the draw is 9/47. So the overall probability of getting a 4-card flush and then completing it is 0.0429172*(9/47) = 0.0082182. So the total probability for a flush is 0.0019654 + 0.0082182 = 0.0101836. The probability that exactly 2 out 5 players receiving a flush is combin(5,2)* 0.01018362*(1-00.0101836)3 = 0.001006, or about 1 in 994.
I need to know the odds of someone getting 4 of a kind during a hand of 7 card stud with five players and one deck of cards? I hope you can help me, and Thank You for your time.
There are combin(52,7)=133,784,560 ways to arrange 7 cards out of 52. The number of 7-card sets including a four of a kind is 13*combin(48,3) = 224,848. The 13 is the number of ranks for the 4 of a kind and the combin(48,3) is the number of ways you can choose 3 cards out of the 48 left. So the probability is 224,848/133,784,560 = 0.0017, or 1 in 595.
When you open a new deck of cards they Ace to King of each suit. What are the odds of taking a shuffled deck of cards and reshuffeling it to the Ace to King state it was originally in?
1 in 52 factorial, or 1 in 80,658,175,170,943,900,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000.
If ten people are each dealt two cards from a single deck what is the probability that two players will get a pair of aces?
First, there are 10*9/2=45 ways you can choose 2 players out of 10. The probability of two specific players getting four aces is 1/combin(52,4)=1/270725. So the probability of any two players getting a pair of aces is 45/270725=0.0001662.
If seven players each get seven cards, what is the probability at least one person will get a 7-card flush?
The probability of a single player getting a 7-card flush is 4*combin(13,7)/combin(52,7) = 1 in 19491. The probability of at least one player out of 7 getting a 7-card flush is about 1 in 2785.
I know that mathematically anything is possible, but the other night at the casino I think that I witnessed something that would be a billion to 1 shot, not that those don?t ever happen. Here is what happened: In the course of 40 hands (40 single 3 card deals about 8 rounds with 5 players) at a let it ride table 3 four of a kinds were dealt. With a four of a kind being about 4100 to 1 what would be the odds of three of them being dealt within 40 deals? Please answer as this is killing me. Long time fan
For the sake of simplicity let’s assume each hand is dealt from a fresh deck. The probability of a four of a kind is 13*48/combin(52,5) = 624/2598960. The probability of exactly 3 out of 40 four of a kinds is combin(40,3)*p3*(1-p)37 = 1 in 7378135, where p = 624/2598960. So that is more like a 1 in 7 million shot.
First I wanted to tell you how much I look at and love your web site, and admire your math skills. I use 6 decks to deal blackjack, and added 3 jokers for reasons I won’t waste your time with but, what are the odds of dealing all 3 jokers to a player right in a row. Thank you very much.
You’re welcome, thanks for you compliments. The probability of being dealt 3 jokers in a row from a six deck shoe (plus the 3 jokers) is 1/combin(315,3) = 1 in 5,159,805. Another solution is (3/315)*(2/314)*(1/313).
What are the odds of passing out 13 cards each to four players using a 52 card deck and all four player have a straight from Ace to two? The cards don’t have to be in the same suit.
The answer is (413/COMBIN(52,13))* (313/COMBIN(39,13))* (213/COMBIN(26,13)) = 1 in 61,204,166,001.
What is the probability of being dealt four to a royal?
There are four possible suits for the royal. There are five possible missing cards. The fifth card can be one of 47 other cards. So there are 4*5*47=940 ways to get four to a royal. There are combin(52,5) = 2,598,960 total combinations. So the probability is 940/2,598,960 = 1 in 2,765.
Dear wiz, say a deck of 52 cards is shuffled, and we draw 18 of the 52 cards at random, placing the 18 cards into 6 piles of 3 cards each. What is the probability that one of the piles contains exactly 3 (of the 4) aces?
The easy way to solve the problem is that the probability the first pile has three aces is (4/52)*(3/51)*(2/50) = 1/5525. However each pile has an equal probability of having three aces so we multiply by 6, yielding 6/5525 = 0.001086
What is the probability of getting all face cards in five card stud?
(12/52)*(11/51)*(10/50)*(9/49)*(8/48) = 0.00030474, or about 1 in 3282.
What is the probability of getting two four of a kinds in a two hour period playing Let it Ride?
The probability of a four of a kind in any given hand is 13*48/combin(52,5) = 0.0002401. Let’s assume in two hours you can play 120 hands. The probability of exactly two four of a kinds would be combin(120,2) × 0.00024012 × (1-0.0002401)118 = 0.000400095 = 1 in 2499.41.
In four-card poker, which is more likely a straight or a flush?
Not counting straight flushes and royal flushes the probability of a straight is 1.02% and of a flush is 1.04%. So a flush is slightly more likely.
What is the probability, over the course of 1 million hands, that there is a royal flush drought extending for 200,000 hands? I'm more interested in the solution than the answer itself.
It isn't often I say this but I tried for hours but the math on this one was simply over my head. So I turned to my friend and math professor Gabor Megyesi. Here is his formula for any "drought" problem.
- Let p be the probability of winning any given hand.
- Let d be the length of the drought.
- Let n be the number of hands played.
- Set k=dp and x=np.
- If k=1 then let a=-1, otherwise find a such that k=-ln(-a)/(1+a). (a is a negative number, if k>1 then -1 < a < 0, if k < 1 then a < -1, and a needs to be calculated to high accuracy.) [Wizard’s note: This kind of solution can be easily found in Excel using the Goal Seek feature under the tools menu.]
- if k=1 then let A=2, otherwise let A=(1+a)/(1+ak).
- The probability of no drought of length d in n hands is approximately Aeax.
In this particular problem p=1/40391, d=200000, n=1000000, k=4.9516, x=24.758, a=-0.0073337, A=1.03007. So the probability of no drought is 1.03007*e-0.0073337*24.758 = 0.859042. Thus the probability of at least one drought is 1-0.859042 = 0.140958.
Here is Gabor Megyesi's full 5-page solution (PDF). Thanks Gábor for your help.
I did a random simulation of 32,095 sets of one million hands. The number with at least one drought was 4558, for a probability of 14.20%.
Suppose you have two five-card poker hands dealt from separate decks. You are told hand A contains at least one ace. You are told hand B contains the ace of spades. Which hand is more likely to contain at least one more ace?
The following table shows the probability of 0 to 4 aces in a totally random hand.
Ace Probabilities — Random Hand
| Aces | Formula | Combinations | Probability |
|---|---|---|---|
| 0 | combin(48,5) | 1712304 | 0.658842 |
| 1 | combin(4,1)×combin(48,4) | 778320 | 0.299474 |
| 2 | combin(4,2)×combin(48,3) | 103776 | 0.03993 |
| 3 | combin(4,3)×combin(48,2) | 4512 | 0.001736 |
| 4 | combin(4,4)×combin(48,1) | 48 | 0.000018 |
| Total | 2598960 | 1 |
Take the sum for 1 to 4 aces we see the probability of at least one ace is 0.341158. The probability of two or more aces is 0.041684.
The probability of there being at least one more ace, given there is at least one, can be restated per Bayes' theorem as probability(two more aces given at least one ace) = probability (two or more aces)/probability(at least one ace) = 0.041684/ 0.341158 = 0.122185.
For those rusty on Bayes' Theorem, it states that the probability of A given B equals the probability of A and B divided by the probability of B, or Pr(A given B) = Pr(A and B)/Pr(B).
The next table shows the combinations and probability for each number of other aces given that the ace of spades was removed from the deck.
Ace Probabilities — Ace Removed Hand
| Aces | Formula | Combinations | Probability |
|---|---|---|---|
| 0 | combin(3,0)×combin(48,4) | 194580 | 0.778631 |
| 1 | combin(3,1)×combin(48,3) | 51888 | 0.207635 |
| 2 | combin(3,2)×combin(48,2) | 3384 | 0.013541 |
| 3 | combin(3,3)×combin(48,1) | 48 | 0.000192 |
| Total | 249900 | 1 |
This shows the probability of at least one more ace is 0.221369.
For fun, let's solve it the same question using Bayes' Theorem. Assume that random hands are dealt until one is found containing the ace of spades. The probability of at least one additional ace, given the hand contains the ace of spades, could be rewritten as probability(at least two aces given ace of spades is in hand). According to Bayes' theorem, this equals Probability(hand contains ace of spades and at least one more ace) / Pr(hand contains ace of spades). We can break up the numerator as Probability(2 aces including ace of spades) + Probability(3 aces including ace of spades) + Probability(4 aces). Using the first table this equals 0.039930×(2/4) + 0.001736×(3/4) + 0.000018 = 0.021285. The probability of the ace of spades is 5/52 = 0.096154. So the probability of at least two aces given the aces of spades is 0.021285/0.096154 = 0.221369.
So the probability of two or more aces given at least one ace is 12.22% and given the ace of spades is 22.14%.
Okay, I believe your numbers but it still doesn’t make sense to me. I should think the probabilities would be equal. What difference does the suit make of the one ace you are given?
Let’s look at another simpler situation. Suppose woman A says "I have two kids and at least one is a boy." Woman B says "I have two kids and the older one is named John." We can assume nobody named John is a girl and no woman gives the same name to more than one kid. Using conditional probability the probability of both kids being a boy of woman A is pr(both boys)/pr(at least one boy) = pr(both boys)/(1-pr(both girls)) = (1/4)/(1-(1/4)) = (1/4)/(3/4) = 1/3. However the probability woman B’s younger kid is a boy, or both kids are boys, is ?, because saying the older child is named John tells us nothing about the younger child.
To make another example suppose you go to Jiffy Lube and they offer two deals for the same price. Deal A is they will check four parts and replace only the first defective one found. Deal B is they will check only one problem and fix it if found. Wouldn’t you rather take deal A? Your car came in with the same number of expected bad parts but the probability of finding a problem is greater under deal A, and thus you will leave with a small number of expected defective parts under that plan. Likewise a test for any ace will probably turn up the only ace, while a test for the ace of spades does not check for the other three suits, leaving them more likely to be aces.
How did you arrive at 2072 for the number of straight flushes utilizing 4 cards out of 5 in Four Card Poker?
First I separated the straight flushes into two types, those with four consecutive suited cards and those with five. The number of five cards straight flushes is the number of suits * number of spans (ace to 10 as lowest card) = 4*10 = 40. Four the four card straight flushes there are 11 different spans (ace to jack as the low card). In the case of the A234 and JQKA straight flushes the fifth card can be one of 47 (52 less the 4 cards already removed and the fifth card which would form a 5 card straight flush, which were already accounted for). So there are 4*2*47=376 straight flushes of span A234 or JQKA. Of the other nine there are 46 possible cards for the fifth card (52 less the 4 cards already removed and two for cards that would form a five-card straight flush). So the number of straight flushes of span 2345 to TJQK are 4*9*46=1656. So the total number of 4-card straight flushes are 40+376+1656=2072.
A flush is 100% possible on the 17th card dealt no matter what. When is a straight 100% possible on what # card dealt?
A straight is guaranteed only with 45 cards. For example your could deal every A, 2, 3, 4, 6, 7, 8, 9, J Q, and K for a total of 44 cards and still not have a straight.
Dear awesome Mr. Wizard of Odds, I am in complete and utter awe of your statistical acumen. Would you by chance be able to calculate for me the probability of a seven card straight - i.e. A,2,3,4,5,6,7 or 2,3,4,5,6,7,8 or 7,8,9,10,jack,queen,king in a seven card stud. We recognize this is not a real poker hand; however it came up when we were playing and we were wondering if it had a lower probability than a normal full house in seven card stud. Cheers, oh knowledgeable one.
How can I refuse after you buttered me up so nicely? First there are combin(52,7) = 133,784,560 ways to choose 7 cards out of 52, without regard to order. There are 8 possible spans for a 7-card straight (the lowest card could be A to 8). If we had 7 different ranks there are 47 = 16384 ways to arrange the suits. Note that this includes all the same suit, which would form a straight flush. So the probability is 8*16,384/133,784,560 = 1 in 1020.6952.
From a single deck if I deal 4 cards what are the odds that at least 1 card is a spade?
The probability of zero spades is (39/52)*(38/51)*(37/50)*(36/49) = 0.303818. So the probability of at least one spade is 1-0.303818 = 0.696182.
In a single-deck game, what is the probability of getting at least one ace and deuce in four cards? This is useful to know for the game of Omaha.
From probability 101 we know Pr(A or B) = Pr(A) + Pr(B) - Pr(A and B). So Pr(A and B) = Pr(A) + Pr(B) - Pr(A or B). Let's let A be getting an ace and B be getting a deuce. Pr(A) = Pr(at least one ace) = 1-Pr(no aces) = 1-combin(48,4)/combin(52,4) = 1-0.7187 = 0.2813. The probability of no deuces would obviously be the same. By the same logic pr(A or B) = Pr(at least one ace or deuce) = 1-Pr(no aces nor deuces) = 1-combin(44,4)/combin(52,4) = 1 - 0.501435 = 0.498565. So the probability of getting at least one ace and deuce is 0.2813 + 0.2813 - 0.498565 = 0.063962.
What are the odds of being dealt the jack of diamonds 27 hands in a row in a six-card game?
The probability of getting it any one hand is 6/52. The probability of getting it 27 hands in a row is (6/52)27 = 1 in 20,989,713,842,161,800,000,000,000.
What is the probability of getting the "dead man’s hand", a two pair of aces and eights?
There are six ways to arrange two suits out of four for each pair. Then there are 44 cards for the singleton. So the number of successful combinations is 6*6*44 = 1584. There are 2,598,960 combinations in total, so the probability is 0.0609%.
I understand you have already answered the probability of getting the "dead man’s hand", a two pair of aces and eights, is 0.0609% on April 3, 2005, but I believe the dead man’s hand is "two black Aces, two black eights and the Queen of clubs" what is the probability of drawing that exact hand from a single standard deck?
There is only one way to get that exact hand. So the probability would be 1 in combin(52,5) or 1 in 2,598,960.
What are the odds/probability of each possible five-card hand that could be dealt for from a standard 52-card deck where the suit of a single, unduplicated card in a hand is considered generic? For example, consider the hand A♠ A♣ A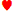 A
A 2. In this hand the suit of the 2 is disregarded and would represent any of the four 2’s in the deck. Another example is A-J-8-6-5. In this hand the suit of all 5 cards is disregarded so that only one such combination can occur. Another example: 3♠ 3
2. In this hand the suit of the 2 is disregarded and would represent any of the four 2’s in the deck. Another example is A-J-8-6-5. In this hand the suit of all 5 cards is disregarded so that only one such combination can occur. Another example: 3♠ 3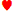 7♣ 7♠ Q. In this hand the suit of the two 3’s and two 4’s is not disregarded because there is more than one in the hand but the suit of the Q is generic. In other words the suit of any card that is not duplicated in a hand is disregarded and that hand is considered to be one of the possible hands even though there would be many possibilities of the hand re-occuring if the suit of each card was not disregarded. Thus a straight or flush made up of five specific cards; say Q
7♣ 7♠ Q. In this hand the suit of the two 3’s and two 4’s is not disregarded because there is more than one in the hand but the suit of the Q is generic. In other words the suit of any card that is not duplicated in a hand is disregarded and that hand is considered to be one of the possible hands even though there would be many possibilities of the hand re-occuring if the suit of each card was not disregarded. Thus a straight or flush made up of five specific cards; say Q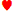 J♣ 10
J♣ 10 9
9 8♠ or A♠ J♠ 8♠ 7♠ 3♠ could only occur once since any other combination of those same cards even though in a different suit would be a duplication. Therefore, using this criteria, what is the O/P of any single hand being dealt? In other words how many such five-card hands exist in a std 52 card deck? Thanks for your input.
8♠ or A♠ J♠ 8♠ 7♠ 3♠ could only occur once since any other combination of those same cards even though in a different suit would be a duplication. Therefore, using this criteria, what is the O/P of any single hand being dealt? In other words how many such five-card hands exist in a std 52 card deck? Thanks for your input.
I’m very familiar with this concept. There are 134,459 unique five-card hands. The reason I know this is my first video poker program analyzed all 2,598,960 possible hands and took days to run through a pay table. However by running just one of each of the 134,459 classes of hands, weighting by the number of all hands in its class, you can cut down the run time by 95%. Sometimes when a game is suit specific like my recent analysis of Black Jack Bonus Poker, I have to dust off my old program and do it the slow way.
What are the probabilities in five card stud using a deck with 5 suits instead of 4?
Combinations in Five Suit Poker
| Hand | Combinations | Probability | Formula |
| Five of a kind | 13 | 0.000002 | 13 |
| Straight flush | 50 | 0.000006 | 5*10 |
| Four of a kind | 3900 | 0.000472 | 13*12*COMBIN(5,4)*5 |
| Flush | 6385 | 0.000773 | 5*(COMBIN(13,5)-10) |
| Full house | 15600 | 0.001889 | 13*12*COMBIN(5,3)*COMBIN(5,2) |
| Straight | 31200 | 0.003777 | 10*(5^5-5) |
| Three of a kind | 214500 | 0.025969 | 13*COMBIN(12,2)*COMBIN(5,3)*5^2 |
| Two pair | 429000 | 0.051938 | COMBIN(13,2)*11*COMBIN(5,2)^2*5 |
| Pair | 3575000 | 0.432815 | 13*COMBIN(12,3)*COMBIN(5,3)*5^3 |
| Nothing | 3984240 | 0.48236 | (COMBIN(13,5)-10)*(5^5-5) |
| Total | 8259888 | 1 |
Note that I reversed the order of the full house and flush.
How many five-card combinations of a standard playing card deck have cards from exactly two suits?
The two suits can be divided either 4 and 1 or 3 and 2. Let’s look at the 4/1 split first. There are 4 suits to choose from for the one with 4 cards, and 3 left for the one with 1 card. There are combin(13,4)=715 ways to choose 4 ranks out of 13. There are 13 ways to choose a single rank. So there are 4×3×715×13=111,540 ways to have a 4/1 split between the two suits. By similar logic there are 4×3×combin(13,3)×combin(13,2)=267,696 ways to have a 3/2 split. So the overall probability is (111540+267696)/combin(52,5) = 14.59%.
What are the odds of being the dealt 2-3-4-5-7 unsuited? Thanks a lot, the site’s great!
Thanks. (45-4)/combin(52,5) = 1020/2598960 = 1 in 2,548.
I was at Foxwoods the other day, watching the final two tables of the Foxwoods Poker Classic. When Vince Van Patten (one of the World Poker Tour hosts) came in to watch, he started making all kinds of prop bets with some of the poker pros who were hanging around. He was offering anyone 20 to 1 if they could flip through an entire deck of cards cycling through the ranks and saying aloud while peeling each card Ace, 2, 3, 4, and so on up to King and starting again at Ace without ever having the card they’re announcing come up. Nobody made it all the way through and Vince won a few hundred dollars in about 10 minutes before everybody gave up. I know this has to be possible, but I have a suspicion Vince has quite the hustle going offering only 20 to 1 on this. What are the odds of actually getting through the whole deck?
A simple way to estimate the probabiity of winning is to assume that every card has a 12/13 probability of not matching the stated rank. To win this bet, the victim would have to do this successfully 52 times. The probability of 52 wins is (12/13)52 = 1.56%. A fair price to pay would be 63.2 to 1. At 20 to 1 Vince had a 67.3% advantage (ouch!).
Accoring to G.M., who is a better mathematician than I am, the actual probabiliy is 1.6232727%. The reason for the difference is the outcome of each pick is positively correlated to previous picks.
Playing last night, one of the players, an old crafty scruffy aggressive player, was challenging the table to make even money side bets on the flop. This old curmudgeon was betting that one of the three cards on the flop would be either an ace, deuce, or jack (sometimes he would change the 3 identifiable cards). What are the odds of this bet? Your sage wisdom would be greatly appreciated.
Before any cards are seen, the probability of any three ranks not appearing on the flop are combin(40,3)/combin(52,3) = 9880/22100 = 44.71%. So this guy had a 10.59% advantage.
Suppose that five cards are dealt from a 52-card deck and the first one is a king. What is the probability of at least one more king? I saw an Ace problem you were doing like this one but I couldn't really follow it. Thank you for any help.
The way I prefer to answer probability questions is to use the combinatorial function. Doing it that way, there are combin(48,4) = 194,580 ways to choose four cards that are not kings out of the 48 non-kings in the deck. There are combin(51,4)=249,900 ways to choose any four cards out of the remaining 51 cards in the deck. So, the probability of getting no kings in the next four cards are 194,580/249,900 = 77.86%. Thus, the probability of getting at least one kind is 100% - 77.86% = 22.14%.
Several people have said that the combinatorial function is probably over the heads of the type of people asking these kinds of simple probability questions. I don’t disagree with that, but a major reason for this site is to try to teach my readers something about math. The combinatorial function is extremely useful in probability, and saves a lot of time. However, the question at hand can be easily answered without it.
The probability the second card is not a king is 48/51. That is because there are 48 non-kings left in the deck, and 51 total cards left. If the second card is not a king, then the probability the third card is also not a king is 47/50 (47 non-kings divided by 50 cards left). Following this to the end, the probability that none of the other four cards are kings is (48/51)×(47/50)×(46/49)×(45/48) = 77.86%. The probability that this is not the case, in other words at least one king, is 100% - 77.86% = 22.14%.
First, choose 5 cards from a single 52-card deck. Second, add their blackjack values (T,J,Q,K = 10, A = 1). What are the odds the sum is even/odd? I would think that with the over-abundance of even cards, the sum would be much more likely to be even.
Surprise, an odd total is more likely at 50.03%, despite 30 of the 52 cards being even. The following table shows the probability of each even/odd split.
Odd/Even Question
| Evens | Odds | Combinations | Probability | Sum |
| 0 | 5 | 15504 | 0.005965 | Odd |
| 1 | 4 | 155040 | 0.059655 | Even |
| 2 | 3 | 565440 | 0.217564 | Odd |
| 3 | 2 | 942400 | 0.362607 | Even |
| 4 | 1 | 719200 | 0.276726 | Odd |
| 5 | 0 | 201376 | 0.077483 | Even |
| Total | 2598960 | 1 |
What are the odds if you draw three cards out of a deck that exactly one of them will be a spade?
The probability the first card is a spade, and the second two are not, is (13/52)×(39/51)×(38/50) = 14.53%. You should then multiply that by 3, because the spade could be any one of the three cards. So the answer is 3×14.53% = 43.59%. For those who prefer the combinatorial function, the answer is 13×combin(39,2)/combin(52,3) = 9,633/22,100 = 43.59%.
Select two random numbers between 0 and 1 (evenly distributed). Now select the smaller of the two. What is the average of the selection? What about the general case of n numbers?
For two numbers, the answer is 1/3, and for n numbers it is 1/(n+1). I posted the solutions to my page of math problems, questions 194 and 195.
You are playing a game that involves three people: (a) yourself, (b) your opponent, and (c) a referee. Each of you picks a real number between 0 and 1 in secret. Once all the numbers have been selected, they are revealed. The player who guessed closest to the referee’s number, without going over, wins. If you are closer, you win $1. If your opponent is closer, you lose $1. If both players go over, or there is a tie, the game is a tie.
Is there a number you can pick that will maximize your expected return, if the other player picks randomly? What if the other player has a strategy too?
I hope you’re happy, I spent all day on the second part, and my answer was still wrong. Lest I deprive my readers of the same joy, I won’t just blurt out the answers here. I broke this into two problems, and posted answers and solutions at mathproblems.info, problems 196 and 197.
If you pick five cards at random from a standard 52-card deck, what is the probability that all four suits will be represented?
There would have to be one suit with two cards, and three with one card each. There are four possible suits for the one that is represented twice. For the suit represented twice, there are combin(13,2)=78 ways to choose 2 ranks out of the 13. For each of the other three suits, there are 13 possible ranks each. So, the total number of combinations is 4 × 78 × 13 × 13 × 13 = 685,464. There are combin(52,5)=2,598,960 ways to choose 5 cards out of 52. So the probability is 685,464/2,598,960 = 26.37%.
What is the probability that any two chosen ranks, for example queen and king, will appear consecutively in a random deck? Somebody challenged me to an even-money bet that it would happen.
According to a random simulation, the probability is 48.64%. So, I would have taken that bet.
Can you recommend a function to map any five cards from a 52-card deck to an integer from 0 to 2,598,959?
Yes. First assign each card a value from 0 to 51. Call the cards c1 to c5, ordering them with c1 as the lowest to c5 as the highest. Then call the following function:
int GetIndex(int c1, int c2, int c3, int c4, int c5)
{
return combin(c5,5) + combin(c4,4)+ combin(c3,3) + combin(c2,2) + combin(c1,1);
}
Where combin returns the traditional value, except if the first value is less than the second value, return 0, as follows:
int combin(int x, int y)
{
if (y>x)
return 0;
else
{
int i,n;
n=1;
for (i=x-y+1; i<=x; i++)
n*=i;
for (i=2; i<=y; i++)
n/=i;
return n;
}
}
If you are doing this to access an array element, load the array as follows.
count=0;
for (c5 = 4; c5 < 52; c5++)
{
for (c4 = 3; c4 < c5; c4++)
{
for (c3 = 2; c3 < c4; c3++)
{
for (c2 = 1; c2 < c3; c2++)
{
for (c1 = 0; c1 < c2; c1++)
{
index_array[count]=WhateverYouWish;
count++;
}
}
}
}
}
What is the probability of drawing 3 out of 10 straight flushes, holding three to a straight flush with one gap?

This is a binomial distribution kind of problem. The general formula is that if the probability of an event is p, and each outcome is independent, then the probability of it happening exactly w out of t trials is combin(t,w)×pw×(1-p)t-w.
In this case, there are 2 ways to make the straight flush. You need the 8 of diamonds and another card of either the 6 or J of diamonds. There are combin(47,2)=1,081 ways to draw 2 cards out of the 47 left in the deck. So, the probability of getting a straight flush in any one hand is 2/1,081 = 0.0018501. The probability of making 3 out of 10 is combin(10,3)×0.00185013×(1-0.0018501)7 = 0.000000750178, or 1 in 1,333,017.
Two 54-card decks (including two jokers) are shuffled together. A player is given half of them. What is the probability that the player got all four red threes?
There are 4 red threes and 104 other cards. There is just one way to get all four red threes. There are combin(104,50)= 1.46691 × 1028 ways the player could get 50 of the other 104 cards. The total number of combinations is combin(108,54)= 2.48578 × 1030. combin(104,50)/combin(108,54) = 0.059012.
If you don't like dealing with such large numbers, here is an alternative solution. Number the four red threes 1 to 4. The probability that the first red three is in the player's stack is 54/108. Now remove the first three. The probability that the player has the second red three is 53/107, because the player has 53 cards left, and there are 107 remaining cards. Likewise, the probability that the player has the third red three is 52/106, and the fourth red three is 51/105. (54/108) × (53/107) × (52/106) × (51/105) = 0.059012.
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
In your December 14, 2010 column you wrote that the AAAAAKK hand, which is specifically mentioned in the house way, may have never occurred in the history of the game. According to another dealer, a player got this hand at the Main Street Station in November 2010.
Interesting. As I wrote, I estimate that hand will occur about once every 23.7 years anywhere in Nevada. I’d say that was one of those times.
Suppose you choose two ranks, for example kings and queens. What is the probability that at least once in a randomly-shuffled 52-card deck a king and queen will be next to each other?
I get 48.6279%. If you're looking to make a bet on it, fair odds on the "yes" would be 1.0564 to 1.
I heard there was a "perfect" game of bridge recently, where each player got 13 cards of one of the four suits. What are the odds of that?
There are also rumors of that happening in a game of whist in Warwickshire in 2011. For the benefit of other readers, this is asking what is the probability of dividing a 52-card deck into four groups of 13 cards each, where each set is composed entirely of the 13 cards of one of the suits.
There are combin(52,13)*combin(39,13)*combin(26,13) = 53,644,737,765,488,800,000,000,000,000 possible ways to arrange 52 cards into four 13 card sets. 4! = 24 would be the number of winning combinations, since you could distribute the four suits to the four players any way you wish. So the odds are equal to 1 in 2,235,197,406,895,370,000,000,000,000. To give that number some perspective, if all 7.5 billion people on earth dealt bridge hands at a rate of one per second, the probability of someone dealing a so-called perfect hand before the sun explodes in 5 billion years is 1 in 16,558.
However, some define a "perfect" hand as just one player getting all 13 cards of any suit. I show the probability of this is 1 in 39,688,347,497 games. This probably does happen once in a while somewhere on earth.
What is the probability in Texas Hold-em of two players having a flush on the same hand with both of them using both of their hole cards?
First, let's determine the number of combinations of player and board cards where this could happen. There are obviously four suits. Then there are combin(13,4)=715 ways you can choose four out of 13 cards of the given suit.
Second, one way this could happen is with three cards of that same suit the players have on the board and the other two among the other 39 cards. There are combin(9,3)=84 ways the board can have three out of the 9 cards left of the chosen suit. Then there are combin(39,2)=741 ways to pick two more cards out of the other 39 in the other three suits. So, there are 84*741=62,244 ways with three of the suit in question on the board.
Third, another way this could happen is with four cards of that same suit the players have on the board and the other one among the other 39 cards. There are combin(9,4)=126 ways the board can have four out of the 9 cards left of the chosen suit. Then there are 39 ways to pick one more card out of the other 39 in the other three suits. However, not all of these will result in both player's using both hole cards. For that condition to be met, the lowest card in the suit in question must be on the board. The probability of that, out of the 8 cards of that suit in play, is 4/8 = 1/2. So, there are 126*39*(1/2)=2,457 ways with four of the suit in question on the board.
Fourth, the last way this could happen is with five cards of that same suit the players have on the board. There are combin(9,5)=126 ways the board can have five out of the 9 cards left of the chosen suit. However, not all of these will result in both player's using both hole cards. For that condition to be met, the lowest two cards in the suit in question must be on the board. The probability of that, out of the 9 cards of that suit in play, is combin(5,2)/combin(9,2) = 10/36 = 5/18. So, there are 126*(5/18)=35 ways with four of the suit in question on the board.
So, the number of combinations where this will happen is 715*(62,244 + 2,457 + 35) = 46,286,240.
The total number of combinations of ways to pick four cards for the player hole cards out of 52 and then 5 more out of the 48 left on the board is combin(52,4)*combin(48,5) = 463,563,500,400.
Thus, the probability is 46,286,240 / 463,563,500,400 = 0.000399395 = 1 in 2,504.
This question was asked and discussed in my forum at Wizard of Vegas.
A casino dealer is working on a new Three Card Poker variant. She takes all the face cards from a standard deck and thoroughly shuffles them. She then deals 3 cards to Player #1, three cards to Player #2, three cards to Player #3, and the final three cards to Player #4. What is the probability that all four hands will contain a straight (J-Q-K of any suit)?
Deal to one player at a time. The proability the first player gets one of each rank is 4^3/combin(12,3) = 64/220.
Assuming the first player got a straight, there is a depleted deck of three of each rank left. The proability the second player gets one of each rank is 3^3/combin(9,3) = 27/84.
Assuming the first two players got a straight, there is a depleted deck of two of each rank left. The proability the third player gets one of each rank is 2^3/combin(6,3) = 8/20.
Assuming the first three players got a straight, there is a depleted deck of one of each rank left. Those three cards obviously form a straight.
Thus, the probability all four players get a straight is (64/220)*(27/84)*(8/20)*1 = 216/5775 = 72/1925 = 3.74%.
This question is asked and discussed in my forum at Wizard of Vegas, beginning with this post.
Supposed I had a 48 card deck, four suits, twelve cards each suit. If I drew 15 cards, what is the probability that I will draw at least one card in each suit?
Let's start with 100% and subtract out the probabilities that result in less than four suits.
What is the probability the 48 cards have no hearts, for example? There are 36 cards that are not a heart. The number of ways to choose 15 cards out of 36 is combin(36,15) = 5,567,902,560. The number of ways to choose 15 cards out of all 48 is 1,093,260,079,344. So the probability of the 15 cards without a heart is 5,567,902,560 / 1,093,260,079,344 = 0.005093.
Next, let's multiply that by four, to get the probability of missing any suit, not just hearts: 4 × combin(36,15)/combin(48,15) = 0.02037174.
However, this double-counts some situations. Consider getting 15 black cards. That would omit both hearts and diamonds. We would have double counted that situation. So, we need to correct for that. There are combin(4,2) = 6 ways to choose two suits out of four. The probability of all 15 cards being any two specific suits is combin(24,15)/combin(48,15) = 1307504/1,093,260,079,344 = 0.00000120. As mentioned, there are six ways to choose two suits out of four, so the number of ways all the cards will be of two suits is 6 × combin(24,15)/combin(48,15) = 0.00000718.
Subracting out what we double counted, we get a probability of two or three suits being represented of 0.02037174 - 0.00000718 = 0.02036456.
Note that we don't need to worry about one suit being represented, because it's impossible to choose 15 cards out of 12.
As a final step, subtract the probability of 2 or 3 suits from 100% to get the probability of all four suits being represented: 1.00000000 - 0.02037174 = 0.97963544.
This question is asked and discussed in my forum at Wizard of Vegas.
If I were to deal 13 cards from a shuffled (presumed random) deck of cards, how many different ranks should I expect to see?
This is a Markov Chain kind of problem if there ever was one.
The following table shows the expected number of ranks with 0 to 4 cards for all number of cards dealt from 1 to 52.
Expected Ranks by Cards Dealt
| Cards | 0 Ranks | 1 Rank | 2 Ranks | 3 Ranks | 4 Ranks | Expected Ranks |
|---|---|---|---|---|---|---|
| 1 | 12.000000 | 1.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 |
| 2 | 11.058824 | 1.882353 | 0.058824 | 0.000000 | 0.000000 | 1.941176 |
| 3 | 10.174118 | 2.654118 | 0.169412 | 0.002353 | 0.000000 | 2.825882 |
| 4 | 9.343577 | 3.322161 | 0.324994 | 0.009220 | 0.000048 | 3.656423 |
| 5 | 8.564946 | 3.893157 | 0.519088 | 0.022569 | 0.000240 | 4.435054 |
| 6 | 7.836014 | 4.373589 | 0.745498 | 0.044178 | 0.000720 | 5.163986 |
| 7 | 7.154622 | 4.769748 | 0.998319 | 0.075630 | 0.001681 | 5.845378 |
| 8 | 6.518655 | 5.087731 | 1.271933 | 0.118319 | 0.003361 | 6.481345 |
| 9 | 5.926050 | 5.333445 | 1.561008 | 0.173445 | 0.006050 | 7.073950 |
| 10 | 5.374790 | 5.512605 | 1.860504 | 0.242017 | 0.010084 | 7.625210 |
| 11 | 4.862905 | 5.630732 | 2.165666 | 0.324850 | 0.015846 | 8.137095 |
| 12 | 4.388475 | 5.693157 | 2.472029 | 0.422569 | 0.023770 | 8.611525 |
| 13 | 3.949628 | 5.705018 | 2.775414 | 0.535606 | 0.034334 | 9.050372 |
| 14 | 3.544538 | 5.671261 | 3.071933 | 0.664202 | 0.048067 | 9.455462 |
| 15 | 3.171429 | 5.596639 | 3.357983 | 0.808403 | 0.065546 | 9.828571 |
| 16 | 2.828571 | 5.485714 | 3.630252 | 0.968067 | 0.087395 | 10.171429 |
| 17 | 2.514286 | 5.342857 | 3.885714 | 1.142857 | 0.114286 | 10.485714 |
| 18 | 2.226939 | 5.172245 | 4.121633 | 1.332245 | 0.146939 | 10.773061 |
| 19 | 1.964946 | 4.977863 | 4.335558 | 1.535510 | 0.186122 | 11.035054 |
| 20 | 1.726771 | 4.763505 | 4.525330 | 1.751741 | 0.232653 | 11.273229 |
| 21 | 1.510924 | 4.532773 | 4.689076 | 1.979832 | 0.287395 | 11.489076 |
| 22 | 1.315966 | 4.289076 | 4.825210 | 2.218487 | 0.351261 | 11.684034 |
| 23 | 1.140504 | 4.035630 | 4.932437 | 2.466218 | 0.425210 | 11.859496 |
| 24 | 0.983193 | 3.775462 | 5.009748 | 2.721345 | 0.510252 | 12.016807 |
| 25 | 0.842737 | 3.511405 | 5.056423 | 2.981993 | 0.607443 | 12.157263 |
| 26 | 0.717887 | 3.246098 | 5.072029 | 3.246098 | 0.717887 | 12.282113 |
| 27 | 0.607443 | 2.981993 | 5.056423 | 3.511405 | 0.842737 | 12.392557 |
| 28 | 0.510252 | 2.721345 | 5.009748 | 3.775462 | 0.983193 | 12.489748 |
| 29 | 0.425210 | 2.466218 | 4.932437 | 4.035630 | 1.140504 | 12.574790 |
| 30 | 0.351261 | 2.218487 | 4.825210 | 4.289076 | 1.315966 | 12.648739 |
| 31 | 0.287395 | 1.979832 | 4.689076 | 4.532773 | 1.510924 | 12.712605 |
| 32 | 0.232653 | 1.751741 | 4.525330 | 4.763505 | 1.726771 | 12.767347 |
| 33 | 0.186122 | 1.535510 | 4.335558 | 4.977863 | 1.964946 | 12.813878 |
| 34 | 0.146939 | 1.332245 | 4.121633 | 5.172245 | 2.226939 | 12.853061 |
| 35 | 0.114286 | 1.142857 | 3.885714 | 5.342857 | 2.514286 | 12.885714 |
| 36 | 0.087395 | 0.968067 | 3.630252 | 5.485714 | 2.828571 | 12.912605 |
| 37 | 0.065546 | 0.808403 | 3.357983 | 5.596639 | 3.171429 | 12.934454 |
| 38 | 0.048067 | 0.664202 | 3.071933 | 5.671261 | 3.544538 | 12.951933 |
| 39 | 0.034334 | 0.535606 | 2.775414 | 5.705018 | 3.949628 | 12.965666 |
| 40 | 0.023770 | 0.422569 | 2.472029 | 5.693157 | 4.388475 | 12.976230 |
| 41 | 0.015846 | 0.324850 | 2.165666 | 5.630732 | 4.862905 | 12.984154 |
| 42 | 0.010084 | 0.242017 | 1.860504 | 5.512605 | 5.374790 | 12.989916 |
| 43 | 0.006050 | 0.173445 | 1.561008 | 5.333445 | 5.926050 | 12.993950 |
| 44 | 0.003361 | 0.118319 | 1.271933 | 5.087731 | 6.518655 | 12.996639 |
| 45 | 0.001681 | 0.075630 | 0.998319 | 4.769748 | 7.154622 | 12.998319 |
| 46 | 0.000720 | 0.044178 | 0.745498 | 4.373589 | 7.836014 | 12.999280 |
| 47 | 0.000240 | 0.022569 | 0.519088 | 3.893157 | 8.564946 | 12.999760 |
| 48 | 0.000048 | 0.009220 | 0.324994 | 3.322161 | 9.343577 | 12.999952 |
| 49 | 0.000000 | 0.002353 | 0.169412 | 2.654118 | 10.174118 | 13.000000 |
| 50 | 0.000000 | 0.000000 | 0.058824 | 1.882353 | 11.058824 | 13.000000 |
| 51 | 0.000000 | 0.000000 | 0.000000 | 1.000000 | 12.000000 | 13.000000 |
| 52 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 13.000000 | 13.000000 |
This question is asked and discussed in my forum at Wizard of Vegas.
Somebody challenged me to the following bet. I get to choose any three ranks from a standard poker deck, writing down my prediction, but keeping it hidden until the end. For example, 7-ace-2. He then offered to bet me even money that he could name at least one of my ranks if he got three guesses. What were my odds of winning?
To win, you opponent has to be incorrect with all three predictions. The first prediction has a 10/13 chance of being incorrect. The second guess has a 9/12 chance of being incorrect, because we can remove the first rank guessed as a possibility. The third guess has an 8/11 chance of being incorrect, because we can remove the first two ranks guessed as a possibility.
All three of these things would have to happen for you to win. Thus, the chances of you winning are (10/13) * (9/12) * (8/11) = 720/1716 = 41.96%.
At even money, the house edge on this bet, from your side, is 16.08% (ouch!).
This question was culled from The Book of Proposition Bets by Owen E'Shea (number 7).
Somebody challenged me to a bet that he could roll a total of 12 with two dice within 27 rolls. If he didn't, I would win even money. Since the probability of rolling a 12 is 1/36, shouldn't it take him 36 rolls on average to roll a 12? It would seem the odds were in my favor if my opponent got only 27 rolls. Am I right or where is the flaw in my math?
The average waiting time between 12's is indeed 36 rolls, including the 12 roll itself. However, that doesn't mean they come along exactly every 36 rolls. The probability of NOT rolling a 12 is (35/36). The probability of not doing so over 27 rolls is (35/36)^27. So, the probability of at least on 12 is 1-(35/36)^27 = 53.26%.
The following table shows the probability of rolling at least on 12 for 20 to 36 rolls. Note that 25 are needed to have an advantage at even money.
Probability 12
| Rolls | Probability |
|---|---|
| 20 | 43.07% |
| 21 | 44.66% |
| 22 | 46.19% |
| 23 | 47.69% |
| 24 | 49.14% |
| 25 | 50.55% |
| 26 | 51.93% |
| 27 | 53.26% |
| 28 | 54.56% |
| 29 | 55.82% |
| 30 | 57.05% |
| 31 | 58.24% |
| 32 | 59.40% |
| 33 | 60.53% |
| 34 | 61.63% |
| 35 | 62.69% |
| 36 | 63.73% |
We know there are combin(52,5)=2,598,960 possible combinations of five cards out of 52. My question is how many possible five-card hands are possible from a five-deck shoe?
Let's take this one type of hand at a time.
- Five of the same card: There are 52 different cards in a deck, for 52 combinations.
- Four of the same card: There are 52 possible cards for the four that are the same and 51 for the singleton. So, there are 52*51 = 2,652 possible combinations for a four of a kind.
- Three of the same card and two of another card: There are 52 possible cards for the three that are the same and 51 for the pair. So, there are 52*51 = 2,652 possible combinations for a full house.
- Three of the same card and two different singletons : There are 52 possible cards for the three that are the same and combin(51,2)=1,275 for the two singletons. So, there are 52*1,275 = 66,300 possible combinations for a three of a kind.
- Two pairs of the same card and one singleton : There are combin(52,2)=1,326 combinations for the two different cards that form pairs. Then there are 50 left for the singleton. So, there are 1,326*50=66,300 possible combinations for a two pair.
- One pair of the same card and three singletons: There are 52 possible cards for the pair. Then there are combin(51,3)=20,825 ways to choose 3 cards out of the 51 left for the singletons. So, the number of combinations for a pair is 52*20,825 = 1,082,900.
- Five singletons: There are combin(52,5)=2,598,960 ways to choose five cards out of 52.
The sum of all these combinations is 3,819,816.
This question is asked and discussed in my forum at Wizard of Vegas.




