Wizard Recommends Cards

Ask The Wizard #413

Is there any way to do a Secret Santa gift exchange that meets the following requirements:

  • Nobody gives a gift to themselves.
  • There are no do-overs.
  • Nobody knows anything except who they are supposed to buy for.
  • Every match is equally likely.

anonymous

Yes! I call the following the Hannah Fry method.

  • Create a set of cards as shown below. Each card should have a unique number on the top and bottom. In the example below, the number is 23.
  • Shuffle the cards and restack them.
  • Keeping the stack in tact, cut each card along the ride line in the middle, creating two stacks.
  • Cut and complete the cut of ONE of the stacks.
  • Distribute the top card of each pile, one at a time, to each participant.
  • Create a numbered list and ask everyone to write their number on it.

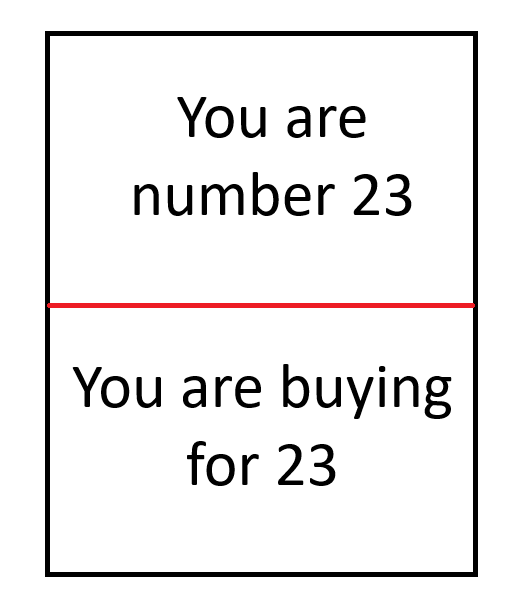
After this procedure has been followed, everyone will have two cards that say, for example, "You are number 13" and "You are buying for number 7." Once the list has been filled out, everyone will know who to buy for, but have no idea who is buying for them.

Source: The Problems with Secret Santa - Numberphile.

A swimming pool is full of salt water.  The pool holds 1000 cubic meters of water.  A garden hose lets fresh water into the pool at a rate of one cubic meter per hour.  As fresh water pours in, water flows out at the other end at the same rate.  How long does it take for the pool to contain only 1% salt water?  

anonymous

The answer is 2000 ln(10) =~ 4605.170186 hours =~ 191.8821 days.

 

Here is my solution (PDF).

On average, how many rolls does it take on each of the platonic solids to roll any side that was previously rolled?

 


Image source: Wikipedia

anonymous

Here is the answer by number of sides.

 

Sides Avg. Rolls
4 3.218750
6 3.774691
8 3.846558
12 5.036074
20 6.293585

 

Let's work out just the case for a six-sided cube.

  • The probability the experiment ends in two rolls is 1/6.
  • The probability the experiment ends in three rolls is (5/6)*(2/6).
  • The probability the experiment ends in four rolls is (5/6)*(4/6)*(3/6).
  • The probability the experiment ends in five rolls is (5/6)*(4/6)*(3/6)*(4/6).
  • The probability the experiment ends in six rolls is (5/6)*(4/6)*(3/6)*(2/6)*(5/6).
  • The probability the experiment ends in seven rolls is (5/6)*(4/6)*(3/6)*(2/6)*(1/6)*(6/6).

Let pr(n) = probability experiment ends in n rolls.

The expected rolls is: 2*pr(2) + 3*pr(3) + 4*pr(4) + 5*pr(5) + 6*pr(6) + 7*pr(7) =

2*(1/6) + 3*(5/6)*(2/6) + 4*(5/6)*(4/6)*(3/6) + 5*(5/6)*(4/6)*(3/6)*(4/6) + 6*(5/6)*(4/6)*(3/6)*(2/6)*(5/6) + 7*(5/6)*(4/6)*(3/6)*(2/6)*(1/6)*(6/6) =~ 3.774691358.