Ask The Wizard #396
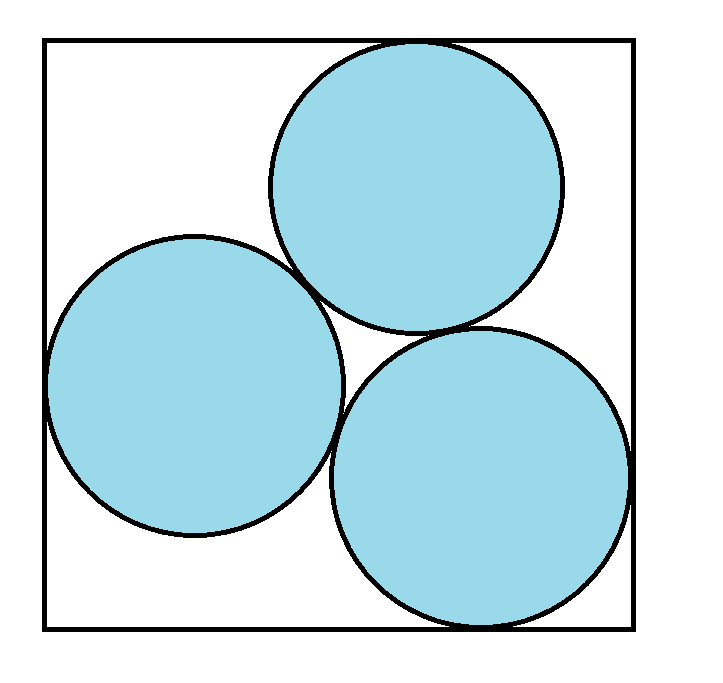
Three circles of radius 1 are inscribed in a square of minimum size. What is the length of a side of the square?
What was the KGB's tell in the movie Rounders?
When there was a significant hand he would pick up an Oreo from a rack he kept of them. Either way, he twisted off one of the cookies. If he had a good hand, he ate it. If he didn't, he put it back in the tray.
In this scene, KGB has the highest possible full house and eats an Oreo.
In this scene, KGB apparently has a straight, a very strong hand in the situation, and eats an Oreo. To be honest, I don't understand why Mike exposed his cards, making a statement he knew the tell.
In this scene, KGB evidently bluffs. Mike goes all in and KGB folds. Then picks up a cookie, but doesn't eat it, implying it was indeed a bluff.
According to my annual win/loss statement, my "coin in" was $1,920,197.60 in video poker in 2023. It was all on $0.25 9-5 Double Double Bonus 5-play. My "coin out" plus jackpots was $1,835,483.75. In other words, my loss was $84,713.83. What is the probability of luck this bad?
The total bet in $0.25 5-play is $6.25. Your number of bets is $1,920,197.60 / $6.25 = 307,232.
The variance per bet is 306.11. The total variance of all your play is 306.11 × 307,232 = $94,045,252. One standard deviation is sqrt( $94,045,252 ) = $9,698.
The expected return of 9-5 Double Double Bonus, assuming perfect play is 0.978729. Your expected loss due to the house edge is $1,920,197.60 × (1-0.978729) = $40,844.52. As mentioned in your question, your actual loss was $84,713.85. That means your loss due to "bad luck" was $84,713.85 - $40,844.52 = $43,869.33.
The number of standard deviations you are down is $43,869.33 / $9,698 = 4.52. The probability of being down that much, or more, is 1 in 329,101.
Not that you asked, but I suspect the reason you are down so much is not all bad luck but partially player error in strategy.
What is your favorite equation for a heart?
(x2 + y2 - 1)3 = x2 y3
Here is a graph of 63 points that fit this equation I did for you.