Ask The Wizard #335
I read about the Reversible Royal game with the 105.22% return in your article at Wizard of Vegas. That return assumes optimal strategy, including for card order. What is the return if I assuming an average royal win? How about if I use ordinary 6-5 Bonus Poker strategy, which is the base pay table?
Assuming no strategy deviations, 1 in 60 royals will be sequential. The reversible royal jackpot pays 161,556 for 1. Any other royal pays 800 for 1. The average royal win is thus (1/60)*161,556 + (59/60)*800 + 17,396 for 1.
If we assuming all royals pay 17,396 and play optimal strategy based on that royal win, then the return drops to 103.56%.
If we play standard 6-5 Bonus Poker strategy, which is the base pay table, then the return drops further to 101.97%.
Consider the unit square with coordinates (0,0), (1,0), (1,1), (0,1). Line A goes from (0,0) to (1,1). Line B goes from (1,0) to 0.5,1). What is the radius of the circle tangent to lines A, B, and the bottom of the circle?
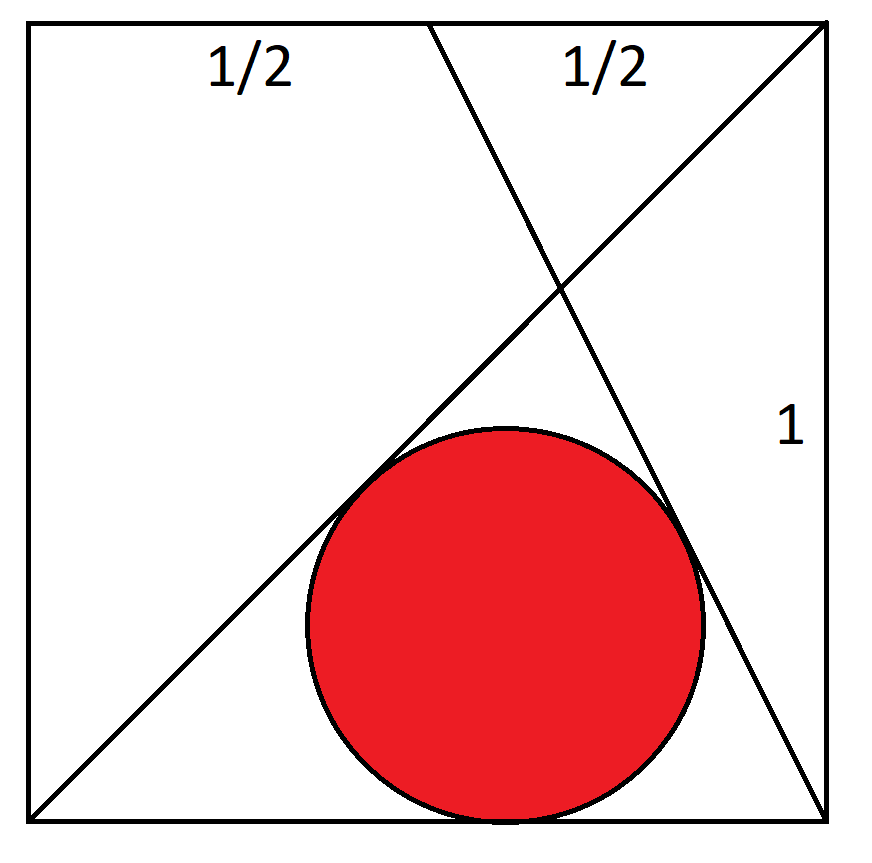
This puzzle appeared in the October 2020 edition of the Mensa Bulletin.
Here is my solution (PDF).
This problem is asked and discussed in my forum at Wizard of Vegas.
What is the probability of getting a Yahtzee if that is the only category you have left on the card?
For the benefit of the readers not familiar with Yahtzee, the question is asking what is the probability of getting a five of a kind in three rolls of five dice. After each roll, you must choose which dice to hold onto and which dice to re-roll.
Here are the possible outcomes after the first roll or any roll where the player rolls 4 or 5 dice.
- Five of a kind = 6*(1/6)^5 = 0.000772
- Four of a kind = (1/6)^3*(5/6)*4 = 0.015432
- Three of a kind = (1/6)^2*(5/6)^2*COMBIN(4,2) = 0.115741
- Two of a kind = 4*(1/6)*(5/6)^3 = 0.385802
- One of a kind = 6*5!/6^5 = 0.092593
Here are the probabilities after holding a pair.
- Five of a kind =(1/6)^3 = 0.004630
- Four of a kind = 3*(1/6)^2*(5/6) = 0.069444
- Three of a kind = 3*(1/6)*(5/6)^2+5*(1/6)^3 = 0.370370
- Two of a kind = (5/6)^3-5*(1/6)^3 = 0.555555
Here are the probabilities after holding a three of a kind:
- Five of a kind =(1/6)^3 = 0.002778
- Four of a kind = 2*(1/6)*(5/6) = 0.27778
- Three of a kind = (5/6)^2 = 0.694444
Here are the probabilities after holding a four of a kind:
- Five of a kind =1/6 = 0.166667
- Four of a kind = 5/6 = 0.83333
With those probabilities of advancement, here are the probabilities of each state after the second roll:
- Five of a kind = 0.000772 + 0.015432*0.166667 + 0.115741*0.002778 + 0.385802*0.004630 + 0.092593* 0.000772 = 0.012631
- Four of a kind = 0.015432*0.166667 + 0.115741*0.27778 + 0.115741*0.27778 = 0.116970
- Three of a kind = 0.115741*0.694444 + 0.385802*0.370370 + 0.092593*0.115741 = 0.409022
- Two of a kind = 0.385802*0.555555 + 0.092593*0.385802 = 0.450103
- One of a kind = 0.092593 * 0.092593 = 0.008573
Using the same probabilities of advancement, here is the probability of a Yahtzee after the third roll:
Five of a kind = 0.012631 + 0.116970*(1/6) + 0.409022*(1/6)^2 + 0.450103*(1/6)^3 + 0.008573*(1/6)^4 = 0.046029.
For those of you who prefer matrix algebra, there is the transition matrix:
| 0.092593 | 0.694444 | 0.192901 | 0.019290 | 0.000772 |
| 0.000000 | 0.555556 | 0.370370 | 0.069444 | 0.004630 |
| 0.000000 | 0.000000 | 0.694444 | 0.277778 | 0.027778 |
| 0.000000 | 0.000000 | 0.000000 | 0.833333 | 0.166667 |
| 0.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 |
If the matrix above is M, then the state after three rolls will be M3, as follows:
| 0.000794 | 0.256011 | 0.452402 | 0.244765 | 0.046029 |
| 0.000000 | 0.171468 | 0.435814 | 0.316144 | 0.076575 |
| 0.000000 | 0.000000 | 0.334898 | 0.487611 | 0.177491 |
| 0.000000 | 0.000000 | 0.000000 | 0.578704 | 0.421296 |
| 0.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 |
The probability of having a Yahtzee after three rolls can be found in the cell in the upper right corner.
After watching through The Queen's Gambit, I noticed none of the games on the show ended in a draw. I thought chess at high levels had lots of draws. For grandmaster-level chess, what percentage of games end in a draw?
According to the article Has the number of draws in chess increased? at ChessBase.com, author Qiyu Zhou states that in 78,468 rated games between players rated games of 2600 or over (it takes 2500 to be a grandmaster), the following are the results:
- Black wins: 18.0%
- White wins: 28.9%
- Draw: 53.1%




