How to apply the PEMDAS rule.
If you’re like me, you get an endless supply of order of operations questions in your Facebook live feed. All of them are followed by hundreds of answers in the comments in which the majority of people are wrong. The number of people who ever admit they were wrong is invariably zero.
What makes my opinion correct? First, if I may toot my own horn, I’d like to think I’m recognized as a leading source of the mathematics of casino games. Search for any casino game or term and you’ll see my name all over the place. Besides that, I have a degree in math and economics from the University of California at Santa Barbara and am a retired associate of the Society of Actuaries. Whatever I have been doing since graduating from college it has been something of a mathematical nature.
An example of such a question is:
6 ÷ 2 (1 + 2) = ?
Pause for a moment and work it out.

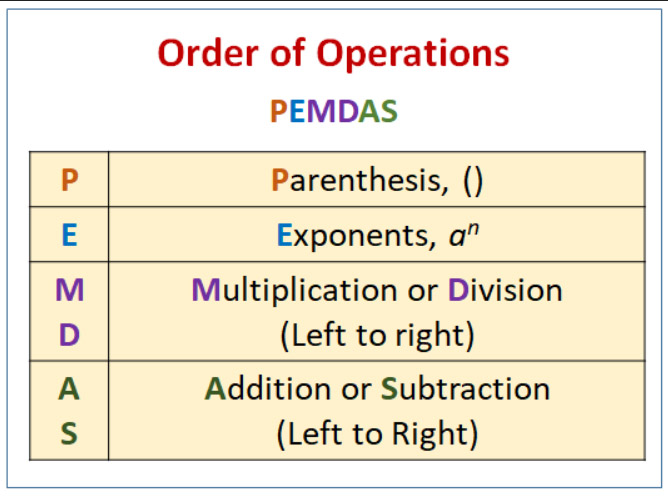
If you got the answer of 1, you are wrong. The reason I suspect you are wrong is you are following the PEMDAS rule of thumb for the order of operations. This is a memory device they teach around 5th grade. A way to remember it I was taught is “Please Excuse My Dear Aunt Sally.” It is meant to teach children to evaluate an expression in the following order:
- 1. Parenthesis
- 2. Exponents
- 3. Multiplication
- 4. Division
- 5. Arithmetic
- 6. Subtraction
Your grammar-school teacher probably truly believed this was correct. However, it’s not. I don’t know where it got started, but I suspect it’s a simplified memory device that 10-year-old children easily understand. The problem with simplifying anything is that while it may lead to the right answer the majority of the time, there are often exceptions to the rule. In the case of PEMDAS, it would lead someone to solve the 6 ÷ 2 (1 + 2) problem stated earlier this way:
- 6 ÷ 2 (1 + 2) = 6 ÷ 2 (3) because you evaluate parenthesis first
- 6 ÷ 2 (3) = 6 ÷ 2 × 3 because no operator outside parenthesis implies multiplication
- 6 ÷ 2 × 3 = 6 ÷ 6 because multiplication is done before division, per PEMDAS
- 6 ÷ 6 = 1
The error in the above logic is in the third step. Multiplication does not always come before division. They are equal in precedence. When both appear in the same expression, do the one further left first.
I might add, addition does not necessarily have to come before subtraction either. Those are also equal in precedence. However, in that case of addition and subtraction, where higher rules don’t apply, it doesn’t matter which you do first.
Here is the correct way to evaluate 6 ÷ 2 (1 + 2):
- 6 ÷ 2 (1 + 2) = 6 ÷ 2 (3) because you evaluate parenthesis first
- 6 ÷ 2 (3) = 6 ÷ 2 × 3 because no operator outside parenthesis implied multiplication
- 6 ÷ 2 × 3 = 3 × 3 because with both multiplication and division, you evaluate from the left first
- 3 × 3 = 9
Here is another question for you:
7 + 7 ÷ 7 + 7 × 7 – 7 = ?
On Facebook you see the answer given as 56. This is one people get wrong not for the reason of PEMDAS, but because “My calculator said the answer is 56.” This is a lazy and incorrect answer given by those who simply go from left to right. The incorrect reasoning is:
- 7 + 7 ÷ 7 + 7 × 7 – 7 = 14 ÷ 7 + 7 × 7 – 7 because you evaluate from the left first
- 14 ÷ 7 + 7 × 7 – 7 = 2 + 7 × 7 – 7 because you evaluate from the left first
- 2 + 7 × 7 – 7 = 9 × 7 – 7 because you evaluate from the left first
- 9 × 7 – 7 = 63 – 7 because you evaluate from the left first
- 63 – 7 = 56
The correct way to evaluate this one is:
- 7 + 7 ÷ 7 + 7 × 7 – 7 = 7 + 1 + 7 × 7 – 7 because division supersedes addition and is to the left of multiplication
- 7 + 1 + 7 × 7 – 7 = 7 + 1 + 49 – 7 because multiplication supersedes addition and subtraction
- 7 + 1 + 49 – 7 = 8 + 49 – 7 because between addition and subtraction do the left-most operation first
- 8 + 49 – 7 = 57 – 7 because between addition and subtraction do the left-most operation first
- 57 – 7 = 50
Note this is one that PEMDAS gets right. People get it wrong for not using their calculators properly. It’s crucial to put in the numbers and operations in the right order. This is much easier to do with calculators that use reverse Polish notation, like the HP15C. By the way, anyone who owns an HP15C or 12C is immediately my friend.
In closing, I would like to add my twist to these order of operations puzzles with this one I created myself, both the logic of the puzzle and the layout. I admit I stole the images off of Google. This puzzle was inspired by a similar, but even harder one, from the Mind Your Decisions YouTube channel. Please post it yourself wherever you like; I’m hoping it will go viral.
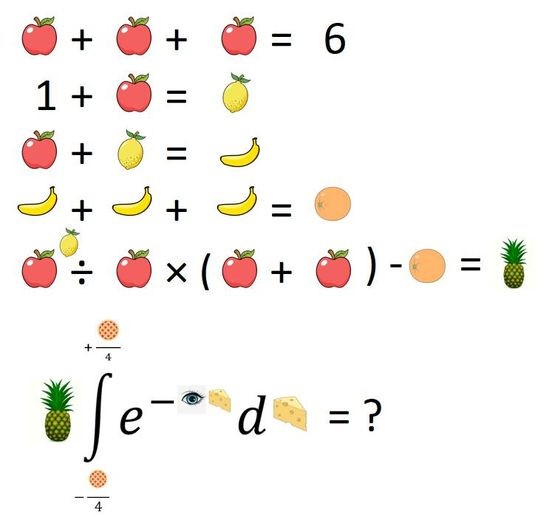
Partial credit for solving for the pineapple only and full credit for solving the integral.
I’ll post the answers in the June 29 newsletter. Until then, may the odds be ever in your favor.




