Large Zoom Call Math Puzzle
The following question was asked in my newsletter last week. In case you need a reminder, here is the question.
Question
Suppose all 435 voting members of the U.S. House of Representatives join in on the same Zoom call, which is scheduled to go from 9 a.m. to 10 a.m.. However, it is not required to attend the entire call, just any part of it. Each member randomly picks an exact moment to enter and leave the call somewhere within that one-hour range.
What is the probability at least one Representative overlaps every other Representative on the call? In other words, seeing the face of every other member during his/her time on the call, not necessarily all at the same time.
Please scroll past these pictures to see my answer and solution.

Answer
2/3
Solution
My general strategy with questions that involve a large group of people is to start with two people. After I find the answer, I go onto three. Then, if it’s not too difficult, I go onto four. If I see a pattern, there the chances are good this pattern will apply for any number of people.
Basic Math Review
Before going further, I’m going to make frequent usage of the combin(x,y) function. This is the number of ways to choose y items out of a group of x. For example, the number of ways to choose five cards out of 52, where order doesn’t matter, is combin(52,5) = 2,598,960. The answer can be expressed as x! / (y! * (x-y)!).
In this case, the exclamation point doesn’t mean I’m yelling, but represents the factorial function. This is the number of ways to order any given number of items. For example, if you have need to read six books, one at a time, the number of possible orders of books is 6!. The answer for the general case of n is 1*2*3*…*n. In the case of the six books, the answer is 1*2*3*4*5*6 = 720.
Two Person Case
That said, let’s solve the problem for the two-person case. The exact times people enter and leave the call does not matter, just the order of the events. Let’s use a letter to represent a particular person entering/leaving the call. Starting from the left, the first usage of a given letter will represent entering the call and the second leaving it.
Of the four spots in the call history, there are combin(4,2)=6 ways you can place the letter A:
1. AABB
2. ABAB
3. ABBA
4. BAAB
5. BABA
6. BBAA
Let’s check whether both callers were on at the same time in each scenario:
1. AABB - No, A came and left before B joined the call.
2. ABAB - Yes, there was overlap between B arriving and A leaving.
3. ABBA - Yes, there was overlap between B arriving and B leaving.
4. BAAB - Yes, there was overlap between A arriving and A leaving.
5. BABA - Yes, there was overlap between A arriving and B leaving.
6. BBAA - No, B came and left before A joined the call.
Each scenario is equally likely. Four out of the six had overlap, thus the probability of overlapping in the two-person case is 2/3.
Three Person Case
The number of call histories in the three-person case is the product of the number of ways person A can choose two spots out of 6 in the history and the number of ways person B can choose 2 out of the 4 remaining spots. This equals combin(6,2)*combin(4,2) = 15*6 = 90.
It would be tedious to list all 90. Let’s simplify things by assuming person A joins first. Somebody must be first, so it may as well be A.
First, let’s consider the situation where the next event in the call history is A leaving. Let’s represent this as AA????. No matter how B and C enter and leave the call, nobody will overlap A. Thus, the AA scenario has a probability of success of 0. The probability of the AA scenario itself is 1/5, because after A took the first spot, there were five possible events to happen next – A, B, B, C, and C.
Second, let’s consider the situation where A joins first, B enters next, and then A leaves. In this case, B represents any person other than A (who already finished the call). This is represented as ABA???. The remaining letters to be placed are B, C, and C. Of the three ways B can be placed (BCC, CBC, and CCB), CBC and CCB result in B overlapping both A and C. Thus, the probability of success in the ABA scenario is 2/3. The probability of that scenario itself is pr(anyone other than A joins)*pr(A leaves) = (4/5)*(1/4) = 1/5, where pr(x) represents the probability of event x.
Third, let’s consider the situation where A joins first, B enters next, and then B leaves. This is represented as ABB???. The remaining letters to be placed are A, C, and C. Of the three ways A can be placed (ACC, CAC, and CCA), CAC and CCA result in A overlapping both B and C. Thus, the probability of success in the ABB scenario is 2/3. The probability of that scenario itself is pr(anyone other than A joins)*pr(B leaves) = (4/5)*(1/4) = 1/5.
Fourth, let’s consider the situation where A joins first, B enters next, and then C joins. This is represented as ABC??? The remaining letters to be placed are A, B, and C. It is easy to see that wherever A leaves the call, he will overlap B and C. So, the probability of success in that scenario is 1. The probability of that scenario itself is pr(anybody other than A joins)*pr(third person joins) = (4/5)*(2/4) = 2/5.
We addressed every possible scenario, as evidenced by the probabilities (1/5 + 1/5 + 1/5 + 2/5) adding up to 1. Taking the dot product of the probability of each scenario and it’s probability of success we get: (1/5)*0 + (1/5)*(2/3) + (1/5)*(2/3) + (2/5)*1 = 0 + 2/15 + 2/15 + 6/15 = 10/15 = 2/3.
Four Person Case
If I were under time pressure, I might guess the answer to the original question is 2/3, since it holds true for the 2 and 3 person cases. However, that seems so unsatisfying, so let’s take it to the four-person case. I can break it down into ten possible scenarios, as follows:
- AA??????
Probability of scenario = 1/7
Probability of success = 0 (nobody can overlap A)
- ABA????
Probability of scenario = 1/7
Probability of success = 16/30
- ABBA????
Probability of scenario = 1/35
Probability of success = 0 (nobody can overlap B)
- ABBC????
Probability of scenario = 4/35
Probability of success = 2/3
- ABCA????
Probability of scenario = 4/35
Probability of success = 5/6
- ABCBA????
Probability of scenario = 1/35
Probability of success = 2/3
- ABCBC????
Probability of scenario = 1/35
Probability of success = 2/3
- ABCBD????
Probability of scenario = 2/35
Probability of success = 1 (A will overlap B, C, and D)
- ABCC????
Probability of scenario = 4/35
Probability of success = 5/6
- ABCD????
Probability of scenario = 8/35
Probability of success = 1 (A will overlap B, C, and D)
I apologize for not going through the math for each situation as carefully, but I didn’t want this solution running too long and wanted to leave some work to the reader.
The following table summarizes all ten scenarios of the four-person case.
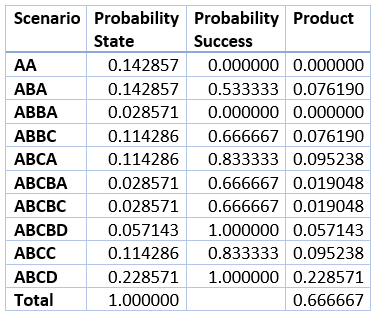
The lower right cell in the table shows a probability of 2/3.
Summary
We have shown a probability of 2/3 for the two-, three-, and four-person cases. It stands to reason that this probability will probably continue to hold for any number of people. Simulations and math by smarter people than me have verified this to be true.




