On this page
3 Dice Football
Introduction
3 Dice Football is a new game I noticed at O'Shea's on April 2, 2011. The game attempts to simulate the game of American football using three dice. The player may bet that a given possession will result in a touchdown or turnover, as well as lots of prop bets on each roll. It is certainly a new concept and I have to give the inventor points for trying something different, as opposed to the usual blackjack and poker variants.
Rules
- At the beginning of a possession, the ball shall start at the defensive 20-yard line. In other words, 20 yards from scoring a touchdown.
- The shooter shall have three rolls (or downs) to advance 10 yards. All rolls, including the neutral and bad ones, count as a down.
- The roll of three dice (two green and one red) shall determine the outcome of each play. Here are the possible outcomes. If more than one are applicable, use the one that appears first.
- If the shooter rolls a three of a kind, then it is an automatic touchdown.
- If the shooter rolls a red 6, and the sum of the green dice is 2 or 3, then it shall result in a turnover, which is a failed attempt at a touchdown.
- If the red die is greater than the sum of the two green dice, then it is considered a penalty, and results in a loss of one yard.
- If the red die is equal to the sum of the two green dice, then no yards are gained.
- If the red die is less than the sum of the two green dice, then the ball shall advance the difference in points. For example, if the green dice were 5 and 6, and the red die was a 3, then the ball would advance 11-3=8 yards.
- If the player advances 10 yards in the first three downs, then he shall get another three downs to advance the rest of the way to a touchdown.
- There are also several prop bets, which win or lose each on each roll.
If that was not clear, here is a scan of the rule cards. As with most images on this site, click on them for a larger version.
 |
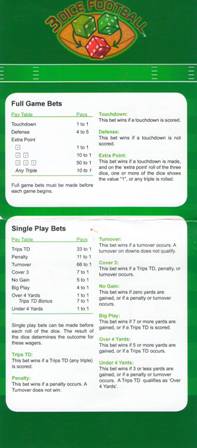 |
Analysis
The primary bet is on a Touchdown. The lower right cell shows a house edge of 3.62%.
Touchdown
| Event | Pays | Combinations | Probability | Return |
|---|---|---|---|---|
| Win | 1 | 48,943,108,116,236 | 0.481913 | 0.481913 |
| Lose | -1 | 52,616,848,552,180 | 0.518087 | -0.518087 |
| Total | 101,559,956,668,416 | 1.000000 | -0.036173 |
Much like in craps, you can be a contrarian. In this case, you can bet on a turnover, which pays 4 to 5. The table below shows a house edge of 6.74%.
Defense
| Event | Pays | Combinations | Probability | Return |
|---|---|---|---|---|
| Win | 0.8 | 52,616,848,552,180 | 0.518087 | 0.414469 |
| Lose | -1 | 48,943,108,116,236 | 0.481913 | -0.481913 |
| Total | 101,559,956,668,416 | 1.000000 | -0.067444 |
Trips Touchdown is a single-roll bet that the next roll will be a touchdown (three of a kind). Wins pay 33 to 1. The lower right cell shows a house edge of 5.56%.
Trips Touchdown
| Event | Pays | Combinations | Probability | Return |
|---|---|---|---|---|
| Win | 33 | 6 | 0.027778 | 0.916667 |
| Lose | -1 | 210 | 0.972222 | -0.972222 |
| Total | 216 | 1.000000 | -0.055556 |
Penalty is a single-roll bet that the next roll will be a penalty (see rules above). Wins pay 11 to 1. The lower right cell shows a house edge of 5.56%.
Penalty
| Event | Pays | Combinations | Probability | Return |
|---|---|---|---|---|
| Win | 11 | 17 | 0.078704 | 0.865741 |
| Lose | -1 | 199 | 0.921296 | -0.921296 |
| Total | 216 | 1.000000 | -0.055556 |
Turnover is a single-roll bet that the next roll will be a turnover (see rules above). Wins pay 66 to 1. The lower right cell shows a house edge of 6.94%.
Turnover
| Event | Pays | Combinations | Probability | Return |
|---|---|---|---|---|
| Win | 66 | 3 | 0.013889 | 0.916667 |
| Lose | -1 | 213 | 0.986111 | -0.986111 |
| Total | 216 | 1.000000 | -0.069444 |
Cover 3 is a single-roll bet that the next roll will be a penalty, turnover, or single-roll touchdown. Wins pay 7 to 1. The lower right cell shows a house edge of 3.70%.
Cover 3
| Event | Pays | Combinations | Probability | Return |
|---|---|---|---|---|
| Win | 7 | 26 | 0.120370 | 0.842593 |
| Lose | -1 | 190 | 0.879630 | -0.879630 |
| Total | 216 | 1.000000 | -0.037037 |
No Gain is a single-roll bet that the next roll will be a zero gain (see above rules). Wins pay 5 to 1. The lower right cell shows a house edge of 2.78%.
No Gain
| Event | Pays | Combinations | Probability | Return |
|---|---|---|---|---|
| Win | 5 | 35 | 0.162037 | 0.810185 |
| Lose | -1 | 181 | 0.837963 | -0.837963 |
| Total | 216 | 1.000000 | -0.027778 |
Big Play is a single-roll bet that the next roll will result in 7 or more yards or a trips touchdown. Wins pay 4 to 1. The lower right cell shows a house edge of 5.09%.
Big Play
| Event | Pays | Combinations | Probability | Return |
|---|---|---|---|---|
| Win | 4 | 41 | 0.189815 | 0.759259 |
| Lose | -1 | 175 | 0.810185 | -0.810185 |
| Total | 216 | 1.000000 | -0.050926 |
Over 4 Yards is a single-roll bet that the next roll will result in 5 or more yards or a trips touchdown. Wins pay 1 to 1, except a trips touchdown pays 7 to 1. The lower right cell shows a house edge of 4.63%.
Over 4 Yards
| Event | Pays | Combinations | Probability | Return |
|---|---|---|---|---|
| Trips TD | 7 | 6 | 0.027778 | 0.194444 |
| Over 4 yards | 1 | 79 | 0.365741 | 0.365741 |
| Lose | -1 | 131 | 0.606481 | -0.606481 |
| Total | 216 | 1.000000 | -0.046296 |
Under 4 Yards is a single-roll bet that the next roll will result in 3 or less yards, a penalty, or a turnover. Wins pay 1 to 1. The lower right cell shows a house edge of 2.78%.
Under 4 Yards
| Event | Pays | Combinations | Probability | Return |
|---|---|---|---|---|
| Win | 1 | 105 | 0.486111 | 0.486111 |
| Lose | -1 | 111 | 0.513889 | -0.513889 |
| Total | 216 | 1.000000 | -0.027778 |
The final table summarizes the house edge for each bet.
House Edge Summary
| Bet | House Edge |
|---|---|
| Touchdown | 3.62% |
| Defense | 6.74% |
| Trips Touchdown | 5.56% |
| Penalty | 5.56% |
| Turnover | 6.94% |
| Cover 3 | 3.70% |
| No Gain | 2.78% |
| Big Play | 5.09% |
| Over 4 Yards | 4.63% |
| Under 4 Yards | 2.78% |
Strategy
Much like craps, the only decision making in 3 Dice Football is what to bet on. The above table shows the lowest house edge, at 2.78%, is on No Gain and Under 4 Yards. However, the Touchdown bet will last over multiple rolls most of the time. So my advice is to bet on a Touchdown and if you must bet the props, stick to No Gain and Under 4 Yards, which will also hedge against a Touchdown.
It deserves to be noted the single-roll prop bets in this game carry a much lower house edge than those in craps.
Acknowledgements
I was lazy with the analysis of this game, and got the probability of a Touchdown and Turnover from the TCS John Huxley web site, which deserve proper attribution for those figures. I did the rest of the math myself, which agrees with the figures at the John Huxley web site.





