Wizard Recommends Cards

On this page

Sic Bo Appendix

Introduction

 


Image take from the Claridge Hotel/Casino rule book. Click on the image to see the rules on the next page.

 

 

 

The purpose ofthis appendix is to derivate the player's edge for thevarious betting options in sic-bo. To make things simple Iuse the player's edge, as opposed to the house edge, becauseit is easier to think of things from the player'sperspective. The player's edge will always be negative, toget the house edge just multiply by -1. The general formulafor the player's edge is the dot product of all possiblereturns and their respective probability. Note that thereare 63=216 possible combinations of the throw ofthree dice.

 

  • Low:

    This bet would have nohouse edge if it were not for the triple exception. Theprobability of a triple 1, 2, or 3 is 3/216. Theprobability of any total between 3 and 10 is 1/2, or108/216. So the probability of a winning triple is108/216 - 3/216 = 105/216. The player's edge is thus(105/216)*(+1) + (111/216)*(-1) = -6/216 =~-2.78%.

  • High: See Low.

     

  • SpecificNumber:

    The probability ofrolling zero of a specific number is (5/6)3 =125/216.
    The probability of rolling one of a specific number is3*(1/6)1*(5/6)2 = 75/216.
    The probability of rolling two of a specific number is3*(1/6)2*(5/6)1 = 15/216.
    The probability of rolling three of a specific number is(1/6)3 = 1/216.
    The player's edge is thus (125/216)*(-1) + (75/216)*(+1)+ (15/216)*(+2) + (1/216)*(+3) = -17/216 =~-7.780%.

  • Total of4:

    There are 3 ways to rolla 4: (1+1+2, 1+2+1, 2+1+1). The player's edge is thus3/216*(+60) + (213/216)*(-1) = -33/216 =-15.278%.

  • Total of5:

    There are 6 ways to rolla 5: (1+1+3, 1+3+1, 3+1+1, 1+2+2, 2+1+2, 2+2+1). Theplayer's edge is thus 6/216*(+30) + (210/216)*(-1) =-30/216 = -13.889%.

  • Total of6:

    There are 10 ways to rolla 6: (1+1+4, 1+4+1, 4+1+1, 1+2+3, 1+3+2, 2+1+3, 2+3+1,3+1+2, 3+2+1, 2+2+2). The player's edge is thus10/216*(+17) + (206/216)*(-1) = -36/216 =-16.667%.

  • Total of7:

    There are 15 ways to rolla 7: (1+1+5, 1+5+1, 5+1+1, 1+2+4, 1+4+2, 2+1+4, 2+4+1,4+1+2, 4+2+1, 1+3+3, 3+1+3, 3+3+1, 2+2+3, 2+3+2, 3+2+2).The player's edge is thus 15/216*(+12) + (201/216)*(-1) =-21/216 = -9.722%.

  • Total of8:

    There are 21 ways to rolla 8: (1-6-6 * 3 ways, 1-2-5 * 6 ways, 1-3-4 * 6 ways,2-2-4 * 3 ways, 2-3-3 * 3 ways). The player's edge isthus 21/216*(+8) + (195/216)*(-1) = -27/216 =-12.500%.

  • Total of9:

    There are 25 ways to rolla 9: (1-2-6 * 6 ways, 1-3-5 * 6 ways, 1-4-4 * 3 ways,2-2-5 * 3 ways, 2-3-4 * 6 ways, 3-3-3 * 1 way). Theplayer's edge is thus 25/216*(+6) + (191/216)*(-1) =-41/216 = -18.982%.

  • Total of10:

    There are 27 ways to rolla 10: (1-3-6 * 6 ways, 1-4-5 * 6 ways, 2-2-6 * 3 ways,2-3-5 * 6 ways, 2-4-4 * 3 ways, 3-3-4 * 3 ways). Theplayer's edge is thus 27/216*(+6) + (189/216)*(-1) =-27/216 = -12.500%.

  • Total of 11: Seetotal of 10

     

  • Total of 12: Seetotal of 9

     

  • Total of 13: Seetotal of 8

     

  • Total of 14: Seetotal of 7

     

  • Total of 15: Seetotal of 6

     

  • Total of 16: Seetotal of 5

     

  • Total of 17: Seetotal of 4

     

  • Twonumbers:

    Lets suppose the twonumbers chosen are 1 and 2. There are 30 combinationsfeaturing a 1 and a 2: 1-2-1 * 3 ways, 1-2-2 * 3 ways,1-2-3 * 6 ways, 1-2-4 * 6 ways, 1-2-5 * 6 ways, 1-2-6 * 6ways. The player's edge is thus 30/216*(+5) +(186/216)*(-1) = -36/216 = -16.667%.

  • Specifictriplet:

    There is only 1 way toroll a specific triplet. The player's edge is thus1/216*(+180) + (215/216)*(-1) = -35/216 =-16.20%.

  • Anytriplet:

    There are 6 ways to rolla triplet. The player's edge is thus 6/216*(+30) +(210/216)*(-1) = -30/216 = -13.889%.

  • Specificpair:

    Lets assume the pair chosen is ones. There are 16 ways two or three of thatnumber can be rolled: 1+1+1, 1+1+2 * 3 ways, 1+1+3 * 3 ways, 1+1+4 * 3 ways, 1+1+5 * 3 ways, 1+1+6 * 3 ways. Theplayer's edge is thus 16/216*(+10) + (200/216)*(-1) = -72/216 = -18.52%.

Following is a formula for s spots over n dice, taken from The Theory of Gambling and Statistical Logic by Richard A. Epstein, formula 5-14.

 

 

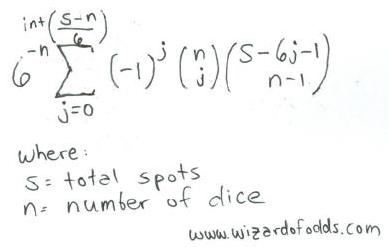
For example, let's look at the number of ways to get 11 spots over 3 dice.

int[(s-n)/6] = int[(11-3)/6] = int[1.33] = 1

The total would be 6-3 * [-10*combin(3,0)*combin(11-6*0-1,3-1) + -11*combin(3,1)*combin(11-6*1-1,3-1) ] =
1/216 * [1*1*combin(10,2) + -1*3*combin(4,2)] =
1/216 * [1*1*45 + -1*3*6] =
1/216 * [45-18] = 27/216 = 12.5%

Written by: Michael Shackleford