On this page
Liberty Stars Keno
Introduction
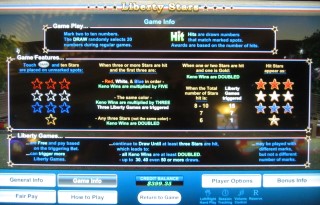
Liberty Stars is a keno-based game found on multi-game machines made by U1 Gaming. I have seen such machines at the Las Vegas Club, Rampart, El Cortez and Dotty's casinos in Las Vegas. The thrust of Liberty Stars is the game randomly places a star on ten of the numbers not chosen by the player. The stars can be red, white, blue, or gold. If the 20 numbers drawn by the game match the star numbers then the player can win multipliers or bonus games.
Rules
- The player chooses 2 to 10 numbers from a range of 1 to 80.
- The game will choose ten numbers randomly from those the player didn't pick and mark them with stars (three red, three white, three blue, and one gold).
- The game will choose 20 numbers from the 1 to 80.
- If a number chosen by the player matches one chosen by the game, then it is called a catch. The player is paid, in part, according to the number of catches.
- If a number marked by a star matches one chosen by the game, then it is called a hit. The player can earn multipliers and bonus games according to the number and pattern of the colors of the stars hit.
- The player can earn multipliers as follows. Only the highest win applies:
- First three stars hit are red, white, and blue, in exact order, wins a 5x multiplier.
- First three stars hit are all the same color wins a 3x multiplier (plus free games — see below).
- At least three stars hit or a gold star wins a 2x multiplier.
- The player can earn bonus games as follows. The player is paid for all earned free spins:
Multiplier Table
Stars
Free Games
8 to 10
15
7
7
6
1
- At least six stars are hit. Free games are paid according to the following table.
- First three stars hit are all the same color wins a 3 free games (plus a 3x multiplier — see above).
- All the same rules apply in free games, except the if the game will draw 20 balls or as many as necessary for the player to have at least three stars, whichever comes last.
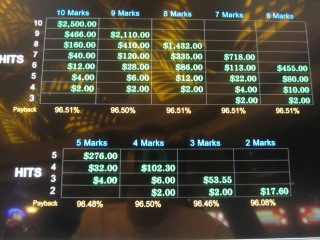
- Following is the base pay table for a $2 wager. In general, the smaller the wager, the smaller the wins.
Pay Table for $2 Bet
Catches
Pick
2
3
4
5
6
7
8
9
10
10
1250
9
1055
233
8
716
205
80
7
359
167.5
60
20
6
227.5
56.5
43
14
6
5
138
40
11
6
3
2
4
51.15
16
5
2
1
1
1
3
26.775
3
2
1
1
0
0
0
2
8.8
1
1
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
- First three stars hit are red, white, and blue, in exact order, wins a 5x multiplier.
- First three stars hit are all the same color wins a 3x multiplier (plus free games — see below).
- At least three stars hit or a gold star wins a 2x multiplier.
Multiplier Table
| Stars | Free Games |
|---|---|
| 8 to 10 | 15 |
| 7 | 7 |
| 6 | 1 |
- At least six stars are hit. Free games are paid according to the following table.
- First three stars hit are all the same color wins a 3 free games (plus a 3x multiplier — see above).
Pay Table for $2 Bet
| Catches | Pick | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 10 | 1250 | ||||||||
| 9 | 1055 | 233 | |||||||
| 8 | 716 | 205 | 80 | ||||||
| 7 | 359 | 167.5 | 60 | 20 | |||||
| 6 | 227.5 | 56.5 | 43 | 14 | 6 | ||||
| 5 | 138 | 40 | 11 | 6 | 3 | 2 | |||
| 4 | 51.15 | 16 | 5 | 2 | 1 | 1 | 1 | ||
| 3 | 26.775 | 3 | 2 | 1 | 1 | 0 | 0 | 0 | |
| 2 | 8.8 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
As with all games by U1 Gaming, there is also a randomly-triggered bonus game, that adds 0.5025% to the return. The following picture shows the pay table and return for a $2 bet.
Examples
Here are some examples to help understand the game. Click on any image for a larger version.
Example 1

In example 1 I bet 5¢ and picked ten numbers. I caught four of them, for a base win of 5¢. In addition, I caught four stars, the first three of which were red, white, and blue, for a 5x multiplier. After considering the multiplier, my final win was 5¢ × 5 = 25¢.
Example 2
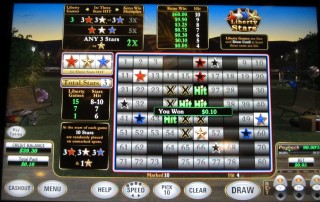
In example 2 I bet 5¢ and picked ten numbers. I caught four of them, for a base win of 5¢. In addition, I caught three stars, one of which was gold. Either of these conditions results in a 2x multiplier. After considering the multiplier, my final win was 5¢ × 2 = 10¢.
Example 3
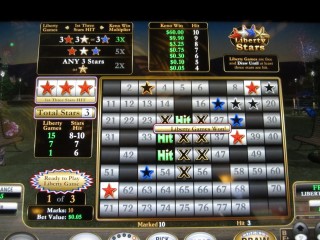
In example 3 I bet 5¢ and picked ten numbers. I caught three of them, which pays 0¢. However, my first three stars caught were all red, which wins a 3x multiplier and 3 free games. Unfortunately, the multiplier didn't help me, but I did earn the free games.
Example 4

Example 4 is from a bonus game. Note that 31 balls were drawn before three stars were hit. The bet on the initiating spin was 5¢. I picked 10 numbers and caught six of them. The win for catching 6 is 6. In addition, the multiplier for three stars (other than certain higher paying combinations) is 2x. . My final win was thus 5¢ × 6 × 2 = 60¢.
Pick 10 Analysis
The following tables are based on the pay table for a $2 bet.
The following table shows the probability of 4 to 10 catches by the number of stars hit.
Probability Table — Catches by Hits
| Catches | Hits | ||||
|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 or More | Total | |
| 4 | 0.008887 | 0.031598 | 0.046366 | 0.060468 | 0.147319 |
| 5 | 0.003792 | 0.012364 | 0.016573 | 0.018698 | 0.051428 |
| 6 | 0.001030 | 0.003069 | 0.003741 | 0.003639 | 0.011479 |
| 7 | 0.000175 | 0.000475 | 0.000523 | 0.000437 | 0.001611 |
| 8 | 0.000018 | 0.000044 | 0.000043 | 0.000031 | 0.000135 |
| 9 | 0.000001 | 0.000002 | 0.000002 | 0.000001 | 0.000006 |
| 10 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| Total | 0.045791 | 0.179571 | 0.295257 | 0.479381 | 1.000000 |
The following table shows the probability of each multiplier, according to the number of stars.
Expected Multiplier by Number of Stars
| Stars | 1 | Gold star | Three or more stars | First three stars same color | Red, white, and blue, in order | Expected multiplier |
|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0.9 | 0.1 | 0 | 0 | 0 | 1.1 |
| 2 | 0.8 | 0.2 | 0 | 0 | 0 | 1.2 |
| 3 | 0 | 0 | 0.9375 | 0.025 | 0.0375 | 2.1375 |
| 4 | 0 | 0 | 0.9375 | 0.025 | 0.0375 | 2.1375 |
| 5 | 0 | 0 | 0.9375 | 0.025 | 0.0375 | 2.1375 |
| 6 | 0 | 0 | 0.9375 | 0.025 | 0.0375 | 2.1375 |
| 7 | 0 | 0 | 0.9375 | 0.025 | 0.0375 | 2.1375 |
| 8 | 0 | 0 | 0.9375 | 0.025 | 0.0375 | 2.1375 |
| 9 | 0 | 0 | 0.9375 | 0.025 | 0.0375 | 2.1375 |
| 10 | 0 | 0 | 0.9375 | 0.025 | 0.0375 | 2.1375 |
The following table shows the return of 4 to 10 catches by the number of stars hit, before considering bonus spins. The lower right cell shows the return, before considering bonus spins, is 54.50%.
Return Table — Catches by Hits
| Catches | Hits | ||||
|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 or More | Total | |
| 4 | 0.008887 | 0.034757 | 0.055639 | 0.129251 | 0.228535 |
| 5 | 0.007583 | 0.027201 | 0.039776 | 0.079935 | 0.154496 |
| 6 | 0.006182 | 0.020256 | 0.026932 | 0.046675 | 0.100045 |
| 7 | 0.003508 | 0.010450 | 0.012563 | 0.018695 | 0.045216 |
| 8 | 0.001425 | 0.003839 | 0.004146 | 0.005267 | 0.014676 |
| 9 | 0.000226 | 0.000547 | 0.000526 | 0.000566 | 0.001865 |
| 10 | 0.000027 | 0.000057 | 0.000049 | 0.000044 | 0.000177 |
| Total | 0.027837 | 0.097108 | 0.139631 | 0.280434 | 0.545010 |
The next table shows the probability of each number of catches in bonus spins, according to whether the player achieved three or more stars within 20 balls, or received extra balls.
Probability Table — Bonus Spins
| Catches | 20 Balls | Extra Balls | Total |
|---|---|---|---|
| 0 | 0.027047 | 0.006576 | 0.033622 |
| 1 | 0.098334 | 0.034798 | 0.133132 |
| 2 | 0.148500 | 0.081995 | 0.230495 |
| 3 | 0.122226 | 0.116219 | 0.238445 |
| 4 | 0.060468 | 0.113659 | 0.174127 |
| 5 | 0.018698 | 0.083640 | 0.102338 |
| 6 | 0.003639 | 0.048960 | 0.052600 |
| 7 | 0.000437 | 0.023271 | 0.023709 |
| 8 | 0.000031 | 0.008761 | 0.008792 |
| 9 | 0.000001 | 0.002381 | 0.002382 |
| 10 | 0.000000 | 0.000357 | 0.000357 |
| Total | 0.479381 | 0.520619 | 1.000000 |
The next table shows the return of each number of catches in bonus spins, according to whether the player achieved three or more stars within 20 balls, or received extra balls. The lower right cell shows that the average win per bonus spin is 6.14. Note how the vast majority of that comes when the player gets more than 20 balls.
Return Table — Bonus Spins
| Catches | 20 Balls | Extra Balls | Total |
|---|---|---|---|
| 0 | 0.000000 | 0.000000 | 0.000000 |
| 1 | 0.000000 | 0.000000 | 0.000000 |
| 2 | 0.000000 | 0.000000 | 0.000000 |
| 3 | 0.000000 | 0.000000 | 0.000000 |
| 4 | 0.129251 | 0.242946 | 0.372197 |
| 5 | 0.079935 | 0.357562 | 0.437497 |
| 6 | 0.046675 | 0.627918 | 0.674593 |
| 7 | 0.014022 | 0.994848 | 1.008870 |
| 8 | 0.004279 | 1.498180 | 1.502459 |
| 9 | 0.000481 | 1.185967 | 1.186448 |
| 10 | 0.000042 | 0.954460 | 0.954502 |
| Total | 0.274686 | 5.861880 | 6.136566 |
As shown above, the probability that the player will get extra balls is 0.520619. If this happens there will always be exactly three stars. In this case there is a 2.5% chance they will be the same color, resulting in three more bonus spins. The expected number of bonus spins from these spins is 52.06% × 2.5% × 3 = 0.039046.
The next table shows those bonus spins that are resolved within 20 by the number of stars. There are never two or less stars, because that would result in extra balls. Each row shows the number of stars, associated probability, the expected number of bonus spins because the first three are the same color, and the number of bonus spins based on having six or more stars. The total column is the expected number of free spins for the given number of stars. The lower right cell shows an expected number of free spins of 0.060836 when a free spin is resolved within 20 balls.
Return Table — Bonus Spins
| Stars | Probability | Same Color | Total Stars | Total |
|---|---|---|---|---|
| 0 | 0.000000 | 0 | 0 | 0.000000 |
| 1 | 0.000000 | 0 | 0 | 0.000000 |
| 2 | 0.000000 | 0 | 0 | 0.000000 |
| 3 | 0.267402 | 0.025 | 0 | 0.020055 |
| 4 | 0.147319 | 0.025 | 0 | 0.011049 |
| 5 | 0.051428 | 0.025 | 0 | 0.003857 |
| 6 | 0.011479 | 0.025 | 1 | 0.012340 |
| 7 | 0.001611 | 0.025 | 7 | 0.011399 |
| 8 | 0.000135 | 0.025 | 15 | 0.002041 |
| 9 | 0.000006 | 0.025 | 15 | 0.000092 |
| 10 | 0.000000 | 0.025 | 15 | 0.000002 |
| Total | 0.479381 | 0.060836 |
So, the expected number of free spins earned per free spin is 0.039046 + 0.060836 = 0.099882.
Considering that bonus spins can earn bonus spins infinitely, the expected number of final bonus spins per initial bonus spin is 1/(1-0.099882) = 1.110966.
As shows before, the expected win per bonus spin, before considering more bonus spins it may earn, is 6.136566. Considering re-spins, the expected win per initial bonus spin is 6.136566 × 1.110966 = 6.817514.
I already shows the expected number of free spins earned when the bonus spin is resolved within 20 balls is 0.060836. This is also going to be true for initial spins, because if there are two or less stars in the first 20 numbers, then player can't earn any bonus spins on an initial spin.
So, on an initial spin the player will earn 0.060836 bonus spins on average. Each one will pay 6.817514 on average, after considering the bonus spins can earn more bonus spins. Thus, the expected return from bonus spins per initial spin is 0.060836 × 6.817514 = 0.414749.
We already showed that the return for immediate wins is 0.545010. Thus, the total return of the game is 0.545010 + 0.414749 = 0.959759.
Finally, as explained in the rules, there is a randomly-triggered bonus that adds another 0.5025% to the game. Thus, all things considered, the return from a $2 pick-10 bet is 0.959759 + 0.005025 = 0.964784. According to the pay table, U1 Gaming gets a return of 96.51%. Personally, I won't lose any sleep over the 0.03% difference.