On this page
Battleship
Introduction
Battleship is a live game by Atmosfera, a software company that provides games for Internet casinos. The game is loosely based on the board game I played thousands of times as a kid. Unlike the board game, every ship in this game, regardless of size, is referred to as a battleship.
Rules
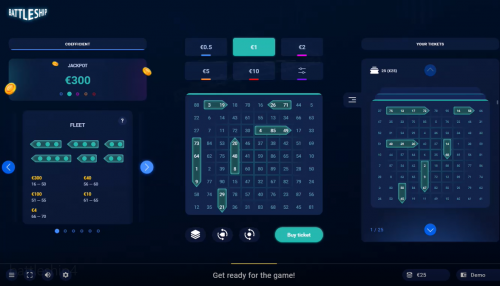
- The game is played on a 10x9 card, with squares numbered from 1 to 90.
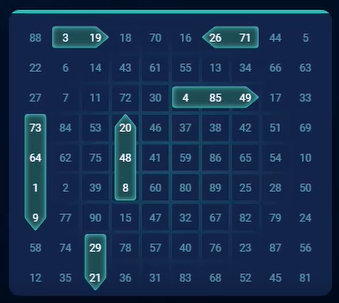
- Each card has placed on it one 4x1 battleship, two 3x1 battleships, and three 2x1 battleships. The player may choose the ship placements himself or let the game do it randomly.
- The player may play 1 to 1,000 cards and choose to bet $0.50 to $5 per card.
- After betting is closed, the game will draw 70 numbers, without replacement, from a hopper containing balls numbered 1 to 90.
- If a ball drawn matches a number on which a battleship lays, then that number shall be considered as “marked.”
- If any battleship is completely marked, then it is said to be sunk.
- The first of four ways to win is called Jackpot, which pays 300 for 1. The player wins if he sinks the 4x1 battleship in the first 10 balls.
- The second of four ways to win is called Battleships. The player wins if he sinks at least two ships that cover 4 to 7 squares between them. The win will depend on the number of squares among the sunken ships and the number of balls needed to do so, as shown in the pay table below.
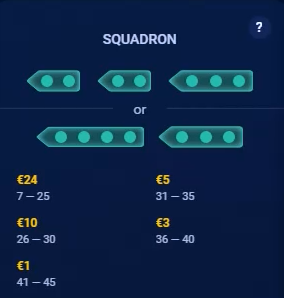
- The third of four ways to win is called Fleet. The player wins according to how many balls are required to sink all six ships. The win depends on the number of balls required to do so.
- The fourth of four ways to win is called Bonus Fleet. The player wins according to how many balls are required to mark every square on every ship, except on square. The win depends on the number of balls required to do so.
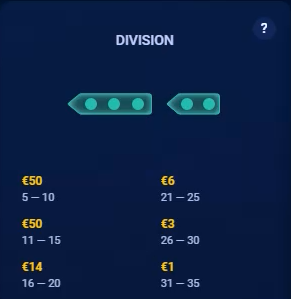
The following table shows the pay table for Battleship wins. As a reminder, four squares are an Echelon, five are a Division, six are a Brigade, and seven are a Squadron.
Battleships Pay Table
| Balls | Echelon | Division | Brigade | Squadron |
|---|---|---|---|---|
| 4 to 10 | 40 | 50 | 60 | 24 |
| 11 to 15 | 12 | 50 | 60 | 24 |
| 16 to 20 | 5 | 14 | 60 | 24 |
| 21 to 25 | 2 | 6 | 16 | 24 |
| 26 to 30 | 1 | 3 | 8 | 10 |
| 31 to 35 | 0 | 1 | 4 | 5 |
| 36 to 40 | 0 | 0 | 2 | 3 |
| 41 to 45 | 0 | 0 | 0 | 1 |
Fleet and Bonus Fleet Pay Table
| Balls | Fleet | Bonus Fleet |
|---|---|---|
| 1 to 50 | 300 | 40 |
| 51 to 55 | 100 | 10 |
| 56 to 60 | 40 | 4 |
| 61 to 65 | 10 | 2 |
| 66 to 70 | 4 | 1 |
Following are screenshots of the pay tables from the game. The screenshot for the Brigade doesn't show a combination of a 4-square and 2-square ship, which does count. Note how the example for the Bonus Fleet is missing a dot from one of the 3-square ships, to show the player needs to get any 15 of the 16 squares.
 |
 |
 |
||
 |
 |
 |
Jackpot Analysis
The probability of sinking the 4x1 battleship within 10 balls is combin(86,6)/combin(90,10) = 1 in 12,168. With a win of 300, the expected return from this feature is 300/12168 = 2.47%.
Battleship Analysis
Echelon Analysis
An Echelon is any two 2x1 battleships, which would cover four squares. With three 2x1 battleships, there are three combinations of choosing 2 out of 3. The following table shows the probability of winning with exactly 4 to 30 balls for any one Echelon, the win, and contribution to the return (product of win and probability).
The lower right cell shows an expected win of 0.027405 per Echelon. With three combinations of Echelons, the total return from Echelons is 3 * 0.027405 = 0.082215
Echelon Analysis
| Balls | Pays | Probability | Return |
|---|---|---|---|
| 4 | 40 | 0.000000 | 0.000016 |
| 5 | 40 | 0.000002 | 0.000063 |
| 6 | 40 | 0.000004 | 0.000157 |
| 7 | 40 | 0.000008 | 0.000313 |
| 8 | 40 | 0.000014 | 0.000548 |
| 9 | 40 | 0.000022 | 0.000877 |
| 10 | 40 | 0.000033 | 0.001315 |
| 11 | 12 | 0.000047 | 0.000564 |
| 12 | 12 | 0.000065 | 0.000775 |
| 13 | 12 | 0.000086 | 0.001033 |
| 14 | 12 | 0.000112 | 0.001343 |
| 15 | 12 | 0.000142 | 0.001709 |
| 16 | 5 | 0.000178 | 0.000890 |
| 17 | 5 | 0.000219 | 0.001096 |
| 18 | 5 | 0.000266 | 0.001331 |
| 19 | 5 | 0.000319 | 0.001597 |
| 20 | 5 | 0.000379 | 0.001896 |
| 21 | 2 | 0.000446 | 0.000892 |
| 22 | 2 | 0.000521 | 0.001041 |
| 23 | 2 | 0.000603 | 0.001205 |
| 24 | 2 | 0.000693 | 0.001386 |
| 25 | 2 | 0.000792 | 0.001584 |
| 26 | 1 | 0.000900 | 0.000900 |
| 27 | 1 | 0.001018 | 0.001018 |
| 28 | 1 | 0.001145 | 0.001145 |
| 29 | 1 | 0.001282 | 0.001282 |
| 30 | 1 | 0.001430 | 0.001430 |
| 31 to 90 | 0 | 0.989275 | 0.000000 |
| Total | 1.000000 | 0.027405 |
Division Analysis
A Division is any one 2x1 battleship and any one 3x1 battleship, which would cover five total squares. With three 2x1 battleships and two 3x1 battleships, there are six ways of chosen one of each size. The following table shows the probability of winning with 5 to 35 balls for any one Division, the win, and contribution to the return (product of win and probability).
The lower right cell shows an expected win of 0.022780 per Division. With three combinations of Echelons, the total return from Divisions 6 * 0.022780 = 0.136681.
Division Analysis
| Balls | Pays | Probability | Return |
|---|---|---|---|
| 4 | 40 | 0.000000 | 0.000016 |
| 5 | 40 | 0.000002 | 0.000063 |
| 6 | 40 | 0.000004 | 0.000157 |
| 7 | 40 | 0.000008 | 0.000313 |
| 8 | 40 | 0.000014 | 0.000548 |
| 9 | 40 | 0.000022 | 0.000877 |
| 10 | 40 | 0.000033 | 0.001315 |
| 11 | 12 | 0.000047 | 0.000564 |
| 12 | 12 | 0.000065 | 0.000775 |
| 13 | 12 | 0.000086 | 0.001033 |
| 14 | 12 | 0.000112 | 0.001343 |
| 15 | 12 | 0.000142 | 0.001709 |
| 16 | 5 | 0.000178 | 0.000890 |
| 17 | 5 | 0.000219 | 0.001096 |
| 18 | 5 | 0.000266 | 0.001331 |
| 19 | 5 | 0.000319 | 0.001597 |
| 20 | 5 | 0.000379 | 0.001896 |
| 21 | 2 | 0.000446 | 0.000892 |
| 22 | 2 | 0.000521 | 0.001041 |
| 23 | 2 | 0.000603 | 0.001205 |
| 24 | 2 | 0.000693 | 0.001386 |
| 25 | 2 | 0.000792 | 0.001584 |
| 26 | 1 | 0.000900 | 0.000900 |
| 27 | 1 | 0.001018 | 0.001018 |
| 28 | 1 | 0.001145 | 0.001145 |
| 29 | 1 | 0.001282 | 0.001282 |
| 30 | 1 | 0.001430 | 0.001430 |
| 31 to 90 | 0 | 0.989275 | 0.000000 |
| Total | 1.000000 | 0.027405 |
Brigade Analysis
A Brigade is any combination of two or three ships which cover six total squares. This could be three 2x1 ships, two 3x1 ships, or the 4x1 ship and a 2x1 ship. There is one 1 way to choose all three 2x1 ships, one way to choose both 3x1 ships, and three ways to choose the 4x1 ship and any one 2x1 ship. The total number of ways this can be achieved is 1+1+3=5. The following table shows the probability of winning with exactly 6 to 40 balls for any one Brigade, the win, and contribution to the return (product of win and probability).
The lower right cell shows an expected win of 0.026373 per Brigade. With five combinations of Brigades, the total return from Brigades 5 * 0.026373 = 0.131867.
Brigade Analysis
| Balls | Pays | Probability | Return |
|---|---|---|---|
| 5 | 50 | 0.000000 | 0.000001 |
| 6 | 50 | 0.000000 | 0.000006 |
| 7 | 50 | 0.000000 | 0.000017 |
| 8 | 50 | 0.000001 | 0.000040 |
| 9 | 50 | 0.000002 | 0.000080 |
| 10 | 50 | 0.000003 | 0.000143 |
| 11 | 50 | 0.000005 | 0.000239 |
| 12 | 50 | 0.000008 | 0.000375 |
| 13 | 50 | 0.000011 | 0.000563 |
| 14 | 50 | 0.000016 | 0.000813 |
| 15 | 50 | 0.000023 | 0.001139 |
| 16 | 14 | 0.000031 | 0.000435 |
| 17 | 14 | 0.000041 | 0.000580 |
| 18 | 14 | 0.000054 | 0.000758 |
| 19 | 14 | 0.000070 | 0.000975 |
| 20 | 14 | 0.000088 | 0.001235 |
| 21 | 6 | 0.000110 | 0.000661 |
| 22 | 6 | 0.000136 | 0.000817 |
| 23 | 6 | 0.000166 | 0.000999 |
| 24 | 6 | 0.000201 | 0.001209 |
| 25 | 6 | 0.000242 | 0.001451 |
| 26 | 3 | 0.000288 | 0.000863 |
| 27 | 3 | 0.000340 | 0.001020 |
| 28 | 3 | 0.000399 | 0.001198 |
| 29 | 3 | 0.000466 | 0.001398 |
| 30 | 3 | 0.000540 | 0.001621 |
| 31 | 1 | 0.000624 | 0.000624 |
| 32 | 1 | 0.000716 | 0.000716 |
| 33 | 1 | 0.000818 | 0.000818 |
| 34 | 1 | 0.000931 | 0.000931 |
| 35 | 1 | 0.001055 | 0.001055 |
| 36+ | 0 | 0.001191 | 0.000000 |
| 36+ | 1.000000 | 0.022780 |
Squadron Analysis
A Squadron is any combination of two or three ships which cover seven total squares. This could be accomplished with two 2x1 and one 3x1 ship or the 4x1 ship and one 3x1 ship. There are three ways to choose 2 out of 3 2x1 ships and two ways to choose one 3x1 ship, for a total of 3*2=6 ways to choose ships in a 2+2+3=7 configuration. There are two ways to choose two out of two 3x1 ships and one way to choose the 4x1 ship, for a total of 2*1 = 2 ways to choose ships in the 4+3 configuration. The total number of ways this can be achieved is 6+2=8. The following table shows the probability of winning with exactly 7 to 45 balls for any one Squadron, the win, and contribution to the return (product of win and probability).
The lower right cell shows an expected win of 0.015128 per Squadron. With five combinations of Squadrons, the total return from Squadrons 8 * 0.015128 = 0.121021.
Squadron Analysis
| Balls | Pays | Probability | Return |
|---|---|---|---|
| 7 | 24 | 0.000000 | 0.000000 |
| 8 | 24 | 0.000000 | 0.000000 |
| 9 | 24 | 0.000000 | 0.000000 |
| 10 | 24 | 0.000000 | 0.000000 |
| 11 | 24 | 0.000000 | 0.000001 |
| 12 | 24 | 0.000000 | 0.000001 |
| 13 | 24 | 0.000000 | 0.000003 |
| 14 | 24 | 0.000000 | 0.000006 |
| 15 | 24 | 0.000000 | 0.000010 |
| 16 | 24 | 0.000001 | 0.000016 |
| 17 | 24 | 0.000001 | 0.000026 |
| 18 | 24 | 0.000002 | 0.000040 |
| 19 | 24 | 0.000002 | 0.000060 |
| 20 | 24 | 0.000004 | 0.000087 |
| 21 | 24 | 0.000005 | 0.000125 |
| 22 | 24 | 0.000007 | 0.000174 |
| 23 | 24 | 0.000010 | 0.000240 |
| 24 | 24 | 0.000014 | 0.000324 |
| 25 | 24 | 0.000018 | 0.000432 |
| 26 | 10 | 0.000024 | 0.000237 |
| 27 | 10 | 0.000031 | 0.000308 |
| 28 | 10 | 0.000040 | 0.000396 |
| 29 | 10 | 0.000050 | 0.000504 |
| 30 | 10 | 0.000064 | 0.000636 |
| 31 | 5 | 0.000079 | 0.000397 |
| 32 | 5 | 0.000099 | 0.000493 |
| 33 | 5 | 0.000121 | 0.000606 |
| 34 | 5 | 0.000148 | 0.000741 |
| 35 | 5 | 0.000180 | 0.000900 |
| 36 | 3 | 0.000217 | 0.000652 |
| 37 | 3 | 0.000261 | 0.000782 |
| 38 | 3 | 0.000311 | 0.000933 |
| 39 | 3 | 0.000370 | 0.001109 |
| 40 | 3 | 0.000437 | 0.001310 |
| 41 | 1 | 0.000514 | 0.000514 |
| 42 | 1 | 0.000602 | 0.000602 |
| 43 | 1 | 0.000702 | 0.000702 |
| 44 | 1 | 0.000816 | 0.000816 |
| 45 | 1 | 0.000945 | 0.000945 |
| 46+ | 0 | 0.993926 | 0.000000 |
| Total | 1.000000 | 0.015128 |
Fleet Analysis
The following table shows my analysis of winning by sinking the entire fleet. The lower right cell shows a return to player of 9.81% of his money bet from this feature.
Fleet Analysis
| Balls | Pays | Probability | Return |
|---|---|---|---|
| 16 | 300 | 0.000000 | 0.000000 |
| 17 | 300 | 0.000000 | 0.000000 |
| 18 | 300 | 0.000000 | 0.000000 |
| 19 | 300 | 0.000000 | 0.000000 |
| 20 | 300 | 0.000000 | 0.000000 |
| 21 | 300 | 0.000000 | 0.000000 |
| 22 | 300 | 0.000000 | 0.000000 |
| 23 | 300 | 0.000000 | 0.000000 |
| 24 | 300 | 0.000000 | 0.000000 |
| 25 | 300 | 0.000000 | 0.000000 |
| 26 | 300 | 0.000000 | 0.000000 |
| 27 | 300 | 0.000000 | 0.000000 |
| 28 | 300 | 0.000000 | 0.000000 |
| 29 | 300 | 0.000000 | 0.000000 |
| 30 | 300 | 0.000000 | 0.000000 |
| 31 | 300 | 0.000000 | 0.000000 |
| 32 | 300 | 0.000000 | 0.000000 |
| 33 | 300 | 0.000000 | 0.000001 |
| 34 | 300 | 0.000000 | 0.000001 |
| 35 | 300 | 0.000000 | 0.000003 |
| 36 | 300 | 0.000000 | 0.000005 |
| 37 | 300 | 0.000000 | 0.000008 |
| 38 | 300 | 0.000000 | 0.000013 |
| 39 | 300 | 0.000000 | 0.000022 |
| 40 | 300 | 0.000000 | 0.000035 |
| 41 | 300 | 0.000000 | 0.000056 |
| 42 | 300 | 0.000001 | 0.000089 |
| 43 | 300 | 0.000001 | 0.000138 |
| 44 | 300 | 0.000002 | 0.000212 |
| 45 | 300 | 0.000003 | 0.000321 |
| 46 | 300 | 0.000005 | 0.000482 |
| 47 | 300 | 0.000007 | 0.000715 |
| 48 | 300 | 0.000011 | 0.001050 |
| 49 | 300 | 0.000016 | 0.001528 |
| 50 | 300 | 0.000023 | 0.002202 |
| 51 | 100 | 0.000033 | 0.001049 |
| 52 | 100 | 0.000048 | 0.001485 |
| 53 | 100 | 0.000069 | 0.002088 |
| 54 | 100 | 0.000098 | 0.002912 |
| 55 | 100 | 0.000139 | 0.004032 |
| 56 | 40 | 0.000194 | 0.002217 |
| 57 | 40 | 0.000270 | 0.003029 |
| 58 | 40 | 0.000372 | 0.004110 |
| 59 | 40 | 0.000511 | 0.005544 |
| 60 | 40 | 0.000697 | 0.007434 |
| 61 | 10 | 0.000945 | 0.002478 |
| 62 | 10 | 0.001273 | 0.003286 |
| 63 | 10 | 0.001707 | 0.004335 |
| 64 | 10 | 0.002276 | 0.005689 |
| 65 | 10 | 0.003019 | 0.007431 |
| 66 | 4 | 0.003985 | 0.003864 |
| 67 | 4 | 0.005235 | 0.005001 |
| 68 | 4 | 0.006846 | 0.006443 |
| 69 | 4 | 0.008912 | 0.008267 |
| 70 | 4 | 0.011553 | 0.010563 |
| 71+ | 0 | 0.988447 | 0.000000 |
| Total | 1.000000 | 0.098136 |
Bonus Fleet Analysis
The following table shows my analysis of winning by sinking the entire fleet, less one square. In other words, 15 out of the 16 numbers covered by ships. The lower right cell shows a return to player of 14.79% of his money bet from this feature.
Bonus Fleet Analysis
| Balls | Pays | Probability | Return |
|---|---|---|---|
| 15 | 40 | 0.000000 | 0.000000 |
| 16 | 40 | 0.000000 | 0.000000 |
| 17 | 40 | 0.000000 | 0.000000 |
| 18 | 40 | 0.000000 | 0.000000 |
| 19 | 40 | 0.000000 | 0.000000 |
| 20 | 40 | 0.000000 | 0.000000 |
| 21 | 40 | 0.000000 | 0.000000 |
| 22 | 40 | 0.000000 | 0.000000 |
| 23 | 40 | 0.000000 | 0.000000 |
| 24 | 40 | 0.000000 | 0.000000 |
| 25 | 40 | 0.000000 | 0.000000 |
| 26 | 40 | 0.000000 | 0.000000 |
| 27 | 40 | 0.000000 | 0.000000 |
| 28 | 40 | 0.000000 | 0.000000 |
| 29 | 40 | 0.000000 | 0.000000 |
| 30 | 40 | 0.000000 | 0.000001 |
| 31 | 40 | 0.000000 | 0.000002 |
| 32 | 40 | 0.000000 | 0.000003 |
| 33 | 40 | 0.000000 | 0.000005 |
| 34 | 40 | 0.000000 | 0.000009 |
| 35 | 40 | 0.000000 | 0.000014 |
| 36 | 40 | 0.000001 | 0.000023 |
| 37 | 40 | 0.000001 | 0.000037 |
| 38 | 40 | 0.000001 | 0.000059 |
| 39 | 40 | 0.000002 | 0.000092 |
| 40 | 40 | 0.000004 | 0.000141 |
| 41 | 40 | 0.000005 | 0.000212 |
| 42 | 40 | 0.000008 | 0.000315 |
| 43 | 40 | 0.000012 | 0.000463 |
| 44 | 40 | 0.000017 | 0.000672 |
| 45 | 40 | 0.000024 | 0.000964 |
| 46 | 40 | 0.000034 | 0.001368 |
| 47 | 40 | 0.000048 | 0.001922 |
| 48 | 40 | 0.000067 | 0.002674 |
| 49 | 40 | 0.000092 | 0.003685 |
| 50 | 40 | 0.000126 | 0.005033 |
| 51 | 10 | 0.000170 | 0.001704 |
| 52 | 10 | 0.000229 | 0.002288 |
| 53 | 10 | 0.000305 | 0.003049 |
| 54 | 10 | 0.000403 | 0.004032 |
| 55 | 10 | 0.000529 | 0.005291 |
| 56 | 4 | 0.000690 | 0.002758 |
| 57 | 4 | 0.000892 | 0.003569 |
| 58 | 4 | 0.001147 | 0.004588 |
| 59 | 4 | 0.001465 | 0.005859 |
| 60 | 4 | 0.001858 | 0.007434 |
| 61 | 2 | 0.002343 | 0.004687 |
| 62 | 2 | 0.002936 | 0.005873 |
| 63 | 2 | 0.003657 | 0.007315 |
| 64 | 2 | 0.004528 | 0.009057 |
| 65 | 2 | 0.005573 | 0.011146 |
| 66 | 1 | 0.006819 | 0.006819 |
| 67 | 1 | 0.008294 | 0.008294 |
| 68 | 1 | 0.010029 | 0.010029 |
| 69 | 1 | 0.012055 | 0.012055 |
| 70 | 1 | 0.014404 | 0.014404 |
| 71+ | 0 | 0.921228 | 0.000000 |
| Total | 1.000000 | 0.147946 |
Summary
The following table shows the contribution to the return from all the elements of the game. The lower right cell shows a total return of 74.25%. To confirm this, I played 900 games, which showed an overall return of 71.63%. I don't think I ever hit the Jackpot in the 900 games. If you remove the 2.47% from the return for not hitting the jackpot, you get 71.78%, which is close to my 900-game return of 71.63%.
Summary
| Way to Win | Return |
|---|---|
| Jackpot | 2.47% |
| Echelon | 8.22% |
| Division | 13.67% |
| Brigade | 13.19% |
| Squadron | 12.10% |
| Fleet | 9.81% |
| Bonus Fleet | 14.79% |
| Total | 74.25% |
Video
In this video I demonstrate the rules of Battleship.