Reason #2 why the Wizard likes Bovada:

No-hassle practice games

Most online casinos spend more effort trying to separate you from your money than they do trying to give you a good experience. They have all kinds of popup windows, they usually make you download their software, and if they do offer play-in-browser games then you have to register an account before you can play. And if you register they start sending you emails trying to get you to deposit real money.

But Bovada is different. They have no popup windows at all, and their practice games play right in your browser, with no download, and no registration required. You don’t even have to give up your email address. It couldn’t be simpler: just one click and you’re playing the game.

I wish all online casinos showed this much respect for their players. Other casinos practically ask for your first born child to play for free. Meanwhile Bovada is patient and does not twist anybody’s arm to play for real money. You can play as long as you like for free with no obligation. The real-money games are available if that’s your preference, but if not, you can play the free practice games for as long as you like without hassle.

Visit Bovada

Ask the Wizard: Blackjack - Basic Strategy (Specific Hands)

Blackjack Menu

» FAQ
» General Questions
» Basic Strategy (General)
» Basic Strategy (Specific Hands)
» Betting Systems
» Blackjack Variants
» Composition-Dependent Strategy
» Counting Cards
» House Edge and Rule Sets
» Multiple Hands / Players
» No Hole Card / No Peek
» Online Blackjack
» Probability
» Shuffling
» Side Bets
» Special Rules and Promotions

wiz, You are the man! You have far and away the best gambling site on the ’net. Being an actuary myself (ACAS), I love to see someone putting their math skills to good use. My question: When late surrender is allowed, do you still want to split 8’s with a ten showing? I’m guessing yes, but one of the hardest plays in BJ is splitting 8’s vs a ten.
As a side note, I just spent 3 days in Vegas, if you haven’t done so already, you must try the Las Vegas Club and the World’s Most Liberal BJ Rules. Doubling is allowed on 3 or 4 cards, 6 cards <= 21 is an automatic winner, and late surrender. At six decks I figured the house advantage to be .14%. Thanks for all of your hard work!!
— Jim from Bloomington, US

Thanks for the kind words Jim. Yes, you still want to split 8’s even if late surrender is offered. Even if you can’t double after a split you should still decline to surrender. Based on a 2 deck game where you can not double after splitting the expected value of splitting 8’s against a 10 is 0.480673, better than the -0.5 by surrendering.

Contrary to their claim of having the "World’s Most Liberal Blackjack Rules" there are better games right across the street at the Horseshoe or the Golden Gate. According to Scott Kister’s Blackjack Conditions and Specials the house edge at the Las Vegas Club is 0.16% and at the Horseshoe and Golden Gate is less at 0.14%. There are even better games on the Strip where the basic strategy player has an edge of 0.05%. It is the six decks at the Las Vegas Club which work against the player. Don’t feel bad about falling for their marquee, I fell for it myself in my younger days before I knew the effects of rule variations.

With single-deck blackjack, are the cards dealt face-down? And what are the general rules for single-deck? I know you mentioned double downs only on 9-11 or 10-11, but do you know what the general rules are for double-after-split, dealer-hitting-soft-17, etc. for single-deck? I’m a basic strategy player, and wanted to find out just what the rules tend to be for single-deck (I’ve only ever done 6 or 8 deck) so I can prepare the perfect spreadsheet from blackjackinfo.com. Thanks so much for your help!
— Alex from Berkeley, CA

Single deck blackjack rules are usually tight. Cards are dealt face down. In southern Nevada you can usually double on any two cards and in northern Nevada it is often 9-11 or 10-11 only. The dealer will hit a soft 17 almost always and doubling after a split is usually not allowed.

In your Blackjack strategy you surrender 16 against A,10,9. You say to split a pair of 8’s against those cards. I have been told that a pair of 8’s is a 16 and should be surrendered. What do you think?
— Jim from Naples, Florida

Whoever told you to surrender two 8’s gave you incorrect advice. To illustrate why you should split 8’s against a 10 check my blackjack appendix 9b. This shows expected return for any initial situation for any given play. The table shows that splitting 8’s against a 10 in double deck has an expected return of -.4706 if allowed to double after a split. In other words you can expect to lose 47.06% of the initial bet on average.This is less than the 50% you would lose by surrendering. If not allowed to double after a split the rate of return is -.4801, again more than -0.5 . Splitting 8’s against a 9 or ace has an even greater return. I assure that the numbers for other numbers of decks are still more than -0.5 .

If the dealer checks his hole card, and does not have blackjack,why hit a soft 18 against an ace; also, why not double on an 11?
— Randy from Columbus, Ohio

In blackjack there are seldom simple answers. You have to consider everything that could happen and weigh every outcome by their probability. The best play is the one with the greatest expected return. According to my blackjack appendix 9b the expected return in a double deck game of hitting a soft 18 against an ace is -0.1004 and the expected return of standing is -0.1005 . So hitting is just a hair better. 11 against an ace is also a very borderline play. It is actually composition dependent in both single and double decks, in other words depending on which two cards that total 11 determines how to play the hand. However if you don’t wish to memorize the composition dependent basic strategy you should double on 11 against an ace in single and double deck and hit with four or more decks.

Hi there - love your site! If I have blackjack, and the dealer is showing an ace, I am given the option of taking even money or continuing the hand. Should I take the even money or play on?
— Ross from New York, New York

This is another way of looking at the decision to take insurance. The expected return of taking even money is obviously 1.0 units bet. Lets assume an infinite deck of cards for the sake of simplicity. The probability the dealer will have a blackjack is 4/13 and the probability otherwise is 9/13. If the dealer gets a blackjack you push, if not you win 1.5 units. The expected value of not taking insurance is (4/13)*0 + (9/13)*(1.5) = 13.5/13 = 1.0384615, which is greater than 1.0. Thus declining insurance, or even money, and playing the hand is the better bet. In an actual game with a finite number of decks the odds are even better since one 10 is already out of the deck (in your hand) which lowers the dealer’s probability of having a blackjack.

Mike, On my last trip to Vegas, a dealer I’ve come to know said he was "toying with the idea" of standing on a 16 against a dealer’s 7 because only 5 of the 8 cards give the dealer an automatic win. How does this strategy play out?
— Chris from Gaithersburg, Maryland

This would be a bad play. For example my blackjack appendix 9B shows the return both ways by playing 10 and 6 cards against a dealer 7. Hitting has an expected loss of 39.6% of the bet. However standing has an expected loss of 47.89%. There is no easy explanation I can give why hitting is better. You have to consider everything that can happen, weight it by its probability, and take the sum. Overall hitting is much better.

Regarding your exceptions to surrender in appendix six, how should I best adapt it to the Unified Gaming single-deck game with early surrender against the ace? Thanks for any help and great site.
— Dave from Provo, USA

Thanks for the compliment. You should use appendix six only if the dealer is showing a ten in a Unified Gaming blackjack game. There are no exceptions to the Unified Gaming basic strategy when the dealer has an ace showing.

I just came back from Costa Rica. They pay even money on a blackjack. What is this worth to the house and should I double down on 21 versus say a dealer 3-6, since I am only going to get paid 1to1?
— Rick from Jacksonville, USA

If a blackjack only pays even money that increases the house edge by about 2.26%! If you do get a blackjack you should still stand regardless of what the dealer is showing.

Hi, I just looked at your Microgaming blackjack basic strategy card. I notice that on 7,7 you advise that the player not hit against a 10. Why is this, and does this override the advice to hit on 14 against a 10?
— Joseph Teo from Singapore

This is the correct play in all my single deck blackjack strategies. The reason is that the probability of getting a third seven is only 2/49, or about 4.08%. Compare this to the probability in double deck of 6/101 = 5.94%. With the low hope of beating a dealer 20 it is better to hit, or surrender if you can. Yes, this does override my advice to hit 14 against a 10.

Have been a dealer now for 10 years, and trying to get out of it, I can not count how many times I have heard people say, "Always assume their is a 10 in the hole". You and I know this cannot be correct all the time. I understand why they say it, but, what are the odds that it really is a ten, and when the dealer has an Ace up, and checks in the card reader for a blackjack, does not have one, you know definitely it is not a ten. What should you assume it is then?
— Larry from Redwing, Minnesota

I don’t like that expression either. At best it is a memory device to help people remember to hit a stiff hand if the dealer has a 7 to 10 showing. There is no simple rule of thumb that works in all situations.

I was studying your appendix 1 on the blackjack site, and came across something odd. Basic strategy in a six deck game (with double after split, dealer stays on soft 17 etc. - all the usual strip rules), dictates that an A,2 against a dealer 5 is a double-down. Yet, on the appendix, the player’s expected return is HIGHER if you hit, rather than double (compare .1334 for hitting, vs. .126 for doubling). The same is true for an A,4 v. a dealer showing a 4 (compare .0593 for hitting with .0584 for doubling down). All of the other splits and doubles work out. What’s up with these two examples? Thanks in advance.
— Fred from San Diego, USA

Appendix 1 is based on an infinite deck. Both hands you mention are borderline plays and the number of decks affects which play is better. For example A,4 against a 4 favors doubling with 26 decks and hitting with 27 decks. A,2 against a 5 also crosses over somewhere between 8 and an infinite number of decks.

As a BJ player I regularly play with regularly splits 10s vs. bust cards. This move has a positive expectation, but isn’t as profitable as standing pat. Could you please show this friend of mine how much worse splitting 10s is than standing pat, in a neutral deck? Also, lots of BJ players get upset at someone who splits 10s vs. 6, but they often split 2s or 7s vs. 10 themselves. Can you set the record straight on this?
— Brett from Richland, USA

I took great pains to create my blackjack appendices 9A-9H to answer these kinds of questions. For example in a six-deck game where the dealer stands on soft 17 then you would use blackjack appendix 9G. There you can see the expected return by standing on two 10’s against a dealer 6 is 0.702826. The expected return by splitting in this situation is 0.622165. So the player can expect to win an extra 8.07% by standing as opposed to splitting. Don’t pay much stock in what other player’s say or do at the blackjack table, trust my advice and you’ll be in fine shape.

wiz, This is a spliting 8’s against a dealer’s 10 question. Splitting is the is the correct play on single hand basis. However, I believe for the typical BJ player it is better to stand when considering you are doubling the amount of the bet. Why double your bet against such poor, way below average, odds? After all, the goal is to maximize your overall return (i.e, the weighted average of all your bets). Your thoughts please? P.S. Your site’s great and advertising like banner ads and sidebars is understandable but invasive advertising like pop up windows and question prompts that try to force you to another site gets to be a bit much IMO.
— Miami from Baltimore, USA

Although this is a close play standing is the third worst option. Using blackjack appendix 9G we can find the following expected returns:

Stand -.536853
Hit -.535361
Split -.474733
Double -1.07022

Splitting is the best decision because it results in the lowest overall loss for the hand. The expected returns for doubling and splitting are based on the total return for that hand relative to the initial bet. In other words it IS a weighted average. The expected loss for each 8 would be just under half of -.535361.

The chart for Double Exposure indicates to split 10’s against a dealer 13-16. Does this mean that you continue to split additional 10’s? I’ve done this and wound up with 4 hands under 18 which all lost. Luckily I was only playing for fun on an Internet gaming site at the time.
— Joe from San Diego

Yes, you should keep splitting as long as you keep getting tens. Playing one hand and losing does not disprove anything. Millions of hands must be played both ways and the results tabulated to truly know the best play.

On a 4-deck blackjack game if you split aces against 5 or 6, and you get another ace. You should double or hit? (no more splits at this point) I am getting different answers on different sites. So far, I have seen one site double on 5 and 6, one site double on 6 only, and other sites list split on all cases and I assume they didn’t consider this situation. Another question in 4 deck BJ for 10,2 against 4, one site listed a hit. I would like a confirmation from you.
— Larry from Austin, USA

Keep in mind most casinos won’t let you do either. However if you can you should double on the 6 only. This is true whether or not the dealer hits a soft 17. If the dealer stands on a soft 17 the expected returns against a 5 are .162849 by hitting and .148228 by doubling, so hitting is the better play. Against a 6 the expected returns are .189020 by hitting and .196249 by doubling. So doubling is the better play. You can see these numbers for yourself in my blackjack appendix 9e. About your other question, yes in a 4-deck game the player should hit a 10,2 against a 4, but only if the dealer stands on a soft 17. I don’t list 4-deck basic strategy exceptions myself because there are so few and they make such a small difference. Following this exception will help you win more unit every 113396 hands, or lower the house edge by 0.000882%. Not worth the bother of memorizing the exception in my opinion.

In your blackjack appendix 6, concerning late surrender you advised surrendering a 10+5 and 9+6 against dealer’s 10. In the basic strategy of Unified Gaming, you advised hitting 15 against dealer’s 10. I don’t understand why hit instead of surrender in this case because the 9+6 and 10+5 are much more probable way to have 15 than 8+7.
— Moisan from Paris, France

This is an interesting situation. Although you should surrender 5/6 of the time with 15 against a 10 in single deck it is still better to always hit than always surrender. Following is the expected return by hitting each way to compose a 15.

10+5: -.501091
9+6: -.509827
8+7: -.474794

There are 4 ways to make a 10+5 and only 1 each of the other two. So the overall expected return by hitting is 15 against a 10 in single deck is (4/6)*-.501091 + (1/6)*-.509827 + (1/6)*-.474794 = -.498164. In other words the odds just barely favor surrendering a 10,5 and 9,6 but the odds favoring hitting 8,7 by a much wider margin. The reason the 8,7 has the better expected return is all the 5’s and 6’s are still in the deck, resulting in a greater probability of attaining a total of 20 or 21.

My question is about table maximum bets in BJ. Say the posted limit is $200. I bet $200 and I get dealt 8-3. Can I double down, or have I already reached the limit? Or suppose I’m betting $200 and get dealt a pair of aces. Can I split them, turning one hand into two hands?
— Jack from Boston, USA

Yes, you could double or split in those situations. The maximum applies to the initial bet. If the limit were $200 you could also play multiple hands of $200.

I have just read an article that says it’s proper basic strategy to stand on a multiple card 16, containing a 4 or 5, Vs. a dealer’s 10 in a multiple deck (4 or more decks) blackjack game. I checked your web site and I could only find appendixes for multiple card hands in 1 and 2 deck games. Is this article correct?
— Rodney from Clarence, New York

Yes! Good question, even I didn’t know this. The fewer the decks and the greater the number of cards the more this is true. To test the most likely case to favor hitting, 8 decks and only 3 cards, I ran every possible situation through my combinatorial program. The following table displays the results.

Expected Values for 3-card 16 Vs. 10 in 8-deck game
Hand	EV Hit	EV Stand	Best Play	Probability	Return Hit	Return Stand
1/5/10	-0.540978	-0.539872	Stand	0.132024	-0.071422	-0.071276
1/6/9	-0.536558	-0.540151	Hit	0.059837	-0.032106	-0.032321
1/7/8	-0.537115	-0.537003	Stand	0.059837	-0.032139	-0.032133
2/4/10	-0.540947	-0.541	Hit	0.237478	-0.128463	-0.128475
2/5/9	-0.542105	-0.540534	Stand	0.039891	-0.021625	-0.021563
2/6/8	-0.537701	-0.540773	Hit	0.059837	-0.032174	-0.032358
2/7/7	-0.538271	-0.537584	Stand	0.028983	-0.015601	-0.015581
3/3/10	-0.540385	-0.540995	Hit	0.115028	-0.06216	-0.06223
3/4/9	-0.541769	-0.540536	Stand	0.059837	-0.032418	-0.032344
3/5/8	-0.54295	-0.540022	Stand	0.039891	-0.021659	-0.021542
3/6/7	-0.538575	-0.540228	Hit	0.059837	-0.032227	-0.032326
4/4/8	-0.543188	-0.54003	Stand	0.028983	-0.015743	-0.015652
4/5/7	-0.544396	-0.539483	Stand	0.039891	-0.021717	-0.021521
4/6/6	-0.539446	-0.542878	Hit	0.028983	-0.015635	-0.015735
5/5/6	-0.545033	-0.542137	Stand	0.009661	-0.005266	-0.005238
Total				1	-0.540355	-0.540293

The two right numbers in the bottom row show that the overall expected value for hitting is -0.540355 and for standing is -0.540293. So standing is the marginally better play. Following this rule will result in an extra unit once every 1117910 hands. It would take about 5 years playing blackjack 40 hours a week before this piece of advice saved the player one unit.

I like to use your blackjack appendix 3 to fine tune my play in online single deck blackjack. I see you have updated this page in December, and it seems like there are a few new moves in the 2-card section. I don’t understand the advice to hit a 10 & 2 against a 4, and particularly against a 6 when the dealer is so likely to bust. And can it really be right to hit these, but not 10 & 2 against a 5?! I’d appreciate any insight you can shed on this. Is the key that the dealer can have an A in the hole with the 6? Hmm, that’s plausible. Are these new strategies, and if so, what brought them about?
— Rich from Londerry, New Hampshire

Yes, I made a couple changes to the two-card list. I removed 9+3 Vs 3 and added 10+2 Vs 6. In a single deck game where the dealer stands on soft 17 and the player has 10+2 against a dealer 6 the expected value of hitting is -0.159436 and for standing is -0.160379. So you lose less on average by hitting. I hate to give sound bite answers to the basic strategy because there are numerous ways the cards can play out. The dealer’s probability of busting is greater with the 6. However as you said the dealer is also more likely to get a 17 with a 6 showing than a 5. A 17 is not a good hand and motivates the player to hit and try to beat it.

If you have 15 and the dealer shows an eight...basic strategy say to hit. In this case, whether you hit or stay your chance of losing is over 70%........why is not the better play to surrender if you are going to lose over 70% of the time no matter if you hit or stay?
— Nino from Glastonbury, USA

For the sake of simplicity let’s stay with your example and say the probability of winning is 70% and losing is 30% if you hit. The expected value of hitting would be 0.3*1 + 0.7*-1 = -0.4. This is greater than the expected value of -0.5 by surrendering.

I just wanted to make sure that the correct play in the Microgaming single deck game of A,A vs A is to split as shown on your basic strategy card. I’m pretty sure the correct play would be to hit, at least with 4 decks, and it just seems that with all the 10’s left you might lose twice your bet pretty often. Not that I don’t believe you but I just wanted to make verify. Any chance you have the EV of hitting vs splitting on this hand?
— William from Pittsburgh, USA

I’ve been questioned about this several times and continue to maintain that despite losing the total bet the option to draw to split aces overcomes the European no-peek rule, thus splitting is the better play. Based on one deck the expected value of each hand (considering the possibility of a dealer blackjack) is -0.532849 for hitting and -0.223277 for splitting. So splitting is better by about 31% of a unit. Splitting is also better for the 4-deck game, which no Microgaming player should be playing since a 1-deck game with the same rules is available.

After performing my own infinite deck analysis for Blackjack with the same rules as yours (dealer stands all 17s, re-splitting allowed to 4 hands except Aces, which can only be split once, doubling after splitting, draw only one card to split Aces), I came across your site. In comparing expected values, I obtained the same numbers as you in all cases, except for pair splitting, which were slightly different. So I’m wondering how you went about your calculation of expected values for splitting?
— Anonymous

It took me years to get the splitting pairs correct myself. Cindy of Gambling Tools was very helpful. Peter Griffin also addresses this topic in chapter 11 of the The Theory of Blackjack Let’s say I want to determine the expected value of splitting eights against a dealer 2. Resplitting up to four hands is allowed. Here is how I did it.

Take a 2 and two 8’s out of the shoe.
Determine the probability that the player will not get a third eight on either hand.
Go through all ranks, except 8, subtract that card from the deck, play out a hand with that card and an 8, determine the expected value, and multiply by 2. For each rank determine the probability of that rank, given that the probability of another 8 is zero. Take the dot product of the probability and expected value over each rank.
Multiply this dot product by the probability from step 2.
Determine the probability that the player will resplit to 3 hands.
Take another 8 out of the deck.
Repeat step 3 but multiply by 3 instead of 2.
Multiply dot product from step 7 by probability in step 5.
Determine the probability that the player will resplit to 4 hands.
Take two more 8’s out of the shoe.
Repeat step 3 but multiply by 4 instead of 2, and this time consider getting an 8 as a third card, corresponding to the situation where the player is forced to stop resplitting.
Multiply dot product from step 11 by probability in step 9.
Add values from steps 4, 8, and 12.
The hardest part of all this is step 3. I have a very ugly subroutine full of long formulas I determine using probability trees. It gets especially ugly when the dealer has a 10 or ace up.

I have a question about the two blackjack strategies your 8 deck blackjack strategy. First off, the underlying assumption before this question is that hitting on a soft 17 is an advantage to the dealer. Why does the strategy have the player double down more often in situations where the dealer might hit a soft 17,i.e, dealer shows an A or 6, but not double down in those same situations when the dealer stands on a soft 17? If hitting a soft 17 gives the house more of an advantage, why would one want to put more money on the table at those times? Is it possible that the two charts are switched?
— Anonymous

You’re right that in general hitting a soft 17 favors the dealer. However this is a generality and not true of every situation. When you have a strong hand of 18 to 21 you want the dealer to stand on a soft 17. However if you have a weak hand under 17 you want the dealer to hit a soft 17. An example of a strategy difference is you should double soft 19 against a 6 when the dealer hits a soft 17, and stand if the dealer stands on soft 17. The reason is that there is a good chance of having drawing a bad card on the double, resulting in 16 or less points. When the dealer hits a soft 17 he busts more often, making doubling a little safer in this example.

You’ve already shown me how to be profitable playing Craps. Thanks! Now your site is teaching me Blackjack. One question: When you’ve got, say, two 5’s and you want to Double Down, you say to put an additional wager next to your original bet. How does the dealer know you don’t mean to split? Thanks! Your site rocks!
— Anonymous

Thank you for the compliment. To answer your question the dealer will just ask you what you want to do. Normally all decisions in blackjack must be visible, however this is the only exception I can think of. However if you want to avoid being asked when it is your turn simply hold up you index finger to denote that you want one card. Most dealers know what this means. Coincidentally I just learned yesterday that in Bulgaria if you wish to double you put your extra bet behind the original bet, and if you want to split you put it next to the original bet.

Another reader wrote in to state that in North Dakota it is the state law to follow the Bulgarian rule for doubling and splitting.

On your Blackjack Basic Strategy chart it says to "Double if allowed, otherwise stand" on A,7 against a dealer’s 3-6. My question is, why stand? If you’re willing to double down but can’t, shouldn’t you at least hit if you can? You were willing to take another card anyway. Thanks for your time!
— Anonymous

If the player had the option to double his bet and stand that would be better than a conventional double. So taking the card actually is detrimental to the player’s hand in these cases, but it worth it to get twice as much money down.

The basic strategy chart for blackjack states to hit on a 16 if the dealer has an ace showing. I was wondering if the chart takes into account the fact that once it is known insurance is not paying then the dealer does not have a 10 value card down? This obviously decreases the dealer’s chance of making a hand, but is it enough that a player should stand on a 16?
— Anonymous

Yes, the basic strategy assumes the dealer does not have a ten in the hole. Even in Europe where the dealer doesn’t check the hit/stand strategy is still the same because if the dealer has a blackjack the player has no hope anyway. When the dealer has an ace, assuming no blackjack, the probability of making 17 or more is 83.3% when the dealer stands on soft 17. So standing is not even a very borderline play, the odds definitely favor hitting.

If the dealer does not check for blackjack with a ten showing, instead taking only the original wager at the end of the hand, does that necessitate any strategy changes?
— Anonymous

No. As long as you stand to lose only the original wager you should play assuming the dealer does not have a blackjack. If the dealer does have blackjack there is nothing you can do about it anyway.

You make a good mathematical argument that the player should refuse insurance. However you don’t make a good psychological argument. Most people would feel like a fool giving up a bird in the hand to lose a shot at 1.5 birds in the bush.
— Anonymous

Oy. Gambling is about taking risks. The successful gambler does not try to maximize his probability of a net win each hand but takes risks to maximize his overall return. Both in gambling and in life one must sometimes take short term risks for long term gain. So think less about the present and more about the future.

Why does your Blackjack Switch basic strategy table say to always hit on 12?
— Anonymous

The player should be more aggressive hitting in Blackjack Switch because a dealer 22 results in a push. Much of the value in standing in regular blackjack is realized when the dealer busts. In Blackjack Switch many of those wins are turned into a push, making hitting a better play in comparison.

My wife knows blackjack basic strategy but insists on being a ’hunch’ player. What are the hands that are closest to 50-50 so that my wife can limit her hunch plays to those?
— Anonymous

I’m pretty sure this has already been answered but it is a good question so I’ll take it again. Here are some borderline plays, as evidenced by having a card counting index equal to zero. This list is for multiple decks where the dealer stands on soft 17 and double after a split is allowed. The best play is listed first and an alternative second.

9 against 2 (hit/double)
12 against 4 (stand/hit)
12 against 6 (stand/hit)
16 against 10 (hit/stand)
Soft 13 against 5 (double/hit)
Soft 15 against 4 (double/hit)
3,3 against 2 (split/hit)

I looked up and down on your blackjack section and can’t find out "how" to surrender. I know what it is and all, but do I just grab half my chips and that’s that?
— Anonymous

No, you never touch your chips once the bet has been made until the hand is over. The signal to surrender is to use your index finger and pretend to draw a line along the blackjack table, just behind your bet from left to right. I didn’t even know this until a friend from Europe did just that recently at the table. It is just as good to simply say "surrender."

Why do you say not to double on 10 or 11 against a 9 in Blackjack Switch?
— Anonymous

The reason is if the dealer gets a 22 and you have 21 or less then the hand pushes. This works strongly to the dealers favor and should be a disincentive to put more money on the table by doubling or splitting.

I heard the other day that if you’re playing a 6:5 game (or the even money game at Rio), you should double down when dealt a natural to help offset the lower payout. Is this correct? What would the expected loss be for that play?
— Anonymous

This would be a terrible play. For example if you doubled on a blackjack against a 5 (six decks dealer stands on soft 17) your expected gain would be 0.622362, according to my blackjack appendix 9I. So even in an even money game this would still be an error costing about 38% of the bet.

Wong states in Professional Blackjack on page 23 the following, "If you get to twelve by 10-2 or 2-10 (where 10 means any 10-count card), and two or fewer decks are being used (or seven or fewer if the dealer stands on soft seventeen), you should hit." Is that correct? I can see it for a one or two deck game where composition-dependent strategy has a certain amount of value to it, but he’s saying that you should hit a 10-2/2-10 when SEVEN decks are used (S17)! That doesn’t sound right to me.
— Anonymous

Wong is referring to a player 12 against a dealer 4 and is quoting The Theory of Blackjack, page 176, by Peter Griffin. Yes, he is right. In a seven deck game the expected value by hitting is -0.210820 and standing is -0.211106, so hitting is higher. However with eight decks hitting is -0.2111161 and standing is -0.211100, so standing is higher. This is such a borderline play that the number of decks does make a difference between seven and eight. Here is an even better example. With A-4 against a 4 you should double all the way through 26 decks but hit with 27 or more.

Are there any basic strategy exceptions for doubling and splitting on the Internet when cash back applies to the total amount bet (thus giving the player an extra incentive to double or split). Please assume a cash back rate of 0.1%.
— Anonymous

I could not find any hand where an extra 0.1% would cause a change in strategy. The closest case I could find, based on six decks and the dealer standing on soft 17, is A,4 against a dealer 4. In that hand doubling costs the player just under 0.3% in expected value compared to hitting. So if you can get 0.3% or more then double that hand. Other borderline hands I examined cost the player at least 1% to double or split, and I have never seen cash back that high in blackjack.

In blackjack the strategy for 16 vs. 10 is R,S since once you eliminate the 2-card hands the strategy is stand (not hit) for any number of decks.
— Anonymous

It is true that in general you should stand on 16 vs. 10 with three of more cards. So if my chart was based on the casino offering the surrender option then you would be right. However that assumption is not made. If I changed the key to Rs (surrender if allowed, otherwise stand) then that would imply that the player should stand on a 2-card 16 against a 10 if surrender was not allowed.

In your blackjack appendix 9 you indicate that the player has a positive expectation hitting 10 against a 10? For example with six decks and the player’s 10 is composed of a 6 and 4 you state the player advantage is 0.026796. Won’t both player and dealer hit until 17? This should give the dealer an advantage because the dealer will win if both bust.
— Anonymous

The reason is because the player’s next card could be an ace but not the dealer’s. I stated in the explanation to that appendix that I already assume the dealer does not have a blackjack. That is why the player has a slight edge in that situation, after the dealer peeks and confirms he does not have a blackjack.

The index number of 16 against a 10 in most blackjack counting systems is zero. So if the deck were completely neutral you should stand, because you stand if the count is equal or exceeds the index number. Yet the basic strategy tables tell us to hit. This seems to be a contradiction.
— Anonymous

In all honesty this is an old question but I got a better answer from Chris F.. He correctly says the reason is that when the basic strategy charts are created they assume the player’s first two cards and the dealer’s up card have already been removed from the deck. A good example of this is that in single deck the correct play is to stand on 7,7 against a 10, because half of the sevens in the deck are already gone, and that is what you need to beat a dealer 20 with 3 cards.
In the case of 16 against a 10 the player’s hand is either composed of a 10 and 6 or a 9 and 7. Either way two cards that would bust the player by hitting have been removed. So the deck is slightly rich in small cards that will not bust the player, giving the player an incentive to hit. While this is true I was skeptical because in an infinite deck game the odds still favor hitting. However except in a few Internet casinos an infinite deck is just an abstraction. I was curious what would be the best play in an 8-deck game if the dealer just said without dealing a single card "You have a 16 and I have a 10, but don’t have a blackjack." Using the blackjack analyzer at gamblingtools.net (site no longer exists), I entered eight decks and then carefully depleted the deck of 1 of every card, except only no sixes, and 2 tens. Then I gave the dealer a 10 and myself a 10 and 6. So the player was playing this hand against a neutral deck with 31 of each card A-9 and 124 tens. Here is the expected values:

10+6 vs 10 — Eight Decks

Play Expected Value

Stand -0.5399

Hit -0.5399

Although the expected value numbers are the same the applet highlights standing as the better play, presumably because it is higher beyond four decimal places. It is the same if I remove the following: A,2,3,4,5,6,8,10,10,10 to simulate 9,7 vs 10, because the player is going against the exact same neutral shoe.

It just goes to show how powerful the effect of removal is, even when just three cards in an eight-deck game. Getting back the original question, a zero count reflects a totally neutral deck after the player’s two cards and dealer’s up card have been accounted for. So as I just showed going into a neutral deck the odds favor standing. The reason hitting is correct in an infinite deck is because there is no effect of removal. If you accidentally hit a 16 vs 10 in a neutral shoe, and got a low card, then the dealer would have a better chance of getting a 10 in the hole. This fact is reflected in the higher expected value for standing in an 8-deck game, but would not matter in an infinite deck. For the record, here are the expected values in an infinite deck game:

10+6 vs 10 — Infinite Decks

Play Expected Value

Stand -0.5404

Hit -0.5398

Sometimes the dealer exposes his hole card in blackjack. What is the correct basic strategy when that happens?
— Anonymous

Stanford Wong gives such a basic strategy in his book Basic Blackjack, see table 46. He also said that in 1995 the Bourbon Street casino in Vegas had a promotion in which every 50 minutes the dealer would expose both his cards for five hands. The player advantage during those was about 10%, according to Wong.

Should I use your basic strategy exceptions after splitting?
— Mick

That is a good question. Personally I eyeball the borderline plays based on what has already been played, especially on the second hand to be played. If forced I would say using the exceptions is better than the basic strategy only. However the way the basic strategy exceptions were created was on the initial hand only, so they are not entirely accurate for splitting, because the deck composition will be a little different.

Your strategy cards for Blackjack I presume is basic strategy for the initial cards (player’s first two cards and dealer’s up card). However after hitting or splitting the deck composition has changed and the basic strategy may have changed. What I think would be more appropriate is a basic strategy based on the overall game of blackjack, including after splitting and hitting. Is there any situation where your initial hand basic strategy and one for the overall game are different?
— Arian from Luton

Yes, my basic strategy charts are designed to be the best play based on the first two cards. This is the usual approach to developing the basic strategy. One benefit to this approach is the expected values of each play can be calculated exactly and compared to other sources. However you bring up a valid point. So I asked Don Schlesinger, author of Blackjack Attack, if there were any known play where the best play on the initial hand is different from the best play to maximize the expected value of the overall game of blackjack. He replied that a soft 18 against a dealer ace, in a double-deck game, where the dealer stands on soft 17, was such a play. As my blackjack appendix 9 shows the expected value for standing is -0.100502 and for hitting is -0.100359. So based on the first two cards the odds favor hitting by 0.000143. However there are many more ways to see soft 18 than one ace and one seven. The following table shows all the ways this hand can turn up.

Soft 18 Vs Ace Combinatorial Analysis
Player
cards Conditional
Probability Hit
EV Stand
EV Hit
Return Stand
Return
A7 0.621139169 -0.100359 -0.100502 -0.062336906 -0.062425729
A6A 0.036728229 -0.11202 -0.116009 -0.004114296 -0.004260805
A52 0.146912917 -0.111299 -0.103382 -0.016351261 -0.015188151
A43 0.146912917 -0.114804 -0.103721 -0.01686619 -0.015237955
A5AA 0.001827682 -0.111395 -0.105122 -0.000203595 -0.00019213
A42A 0.016814677 -0.116975 -0.108233 -0.001966897 -0.001819903
A33A 0.007356421 -0.132142 -0.107256 -0.000972092 -0.00078902
A322 0.020470041 -0.134229 -0.11004 -0.002747673 -0.002252523
A4AAA 0.000073486 -0.117554 -0.110984 -0.000008639 -0.000008156
A32AA 0.001028802 -0.134775 -0.112433 -0.000138657 -0.000115671
A222A 0.000709873 -0.136788 -0.114993 -0.000097102 -0.00008163
A3AAAA 0.000002238 -0.135313 -0.114821 -0.000000303 -0.000000257
A22AAA 0.000023502 -0.137312 -0.117376 -0.000003227 -0.000002759
A2AAAAA 0.000000046 -0.137859 -0.119823 -0.000000006 -0.000000006
Total 1 -0.105806844 -0.102374694
Explanation of column titles
Player cards:Cards in player’s hand
Conditional probability: Given that the player has a soft 18 against a dealer ace the probability of the given hand composition.
Hit EV:Expected value by hitting
Stand EV:Expected value by standing
Hit Return:Product of probability and hit expected value
Stand Return:Product of probability and stand expected value
The left two cells of the bottom row show that overall the expected value of hitting is -0.105807 and for standing is -0.102375. So the table shows the odds favor standing by 0.00343.
To confirm these results I ran two simulations under the rules in question, one simulation hitting and one standing on this play. I counted only hands where soft 18 against a dealer ace happened at any time during play. Here are my results.

Soft 18 Vs Ace Simulation
Soft 17 Hands
Played Total
Win Expected
Value
Stand 3857490 -396224 -0.102715
Hit 3208390 -337572 -0.105215
So the simulation shows the odds favor standing by 0.0025 over all possible scenarios where this hand turns up. Thus for practical purposes of playing all hands the best play is to stand, contrary to what my basic strategy chart says.

Hi, I just stumbled onto your site, and I think it’s a fabulous site for blackjack info. I have a question, though. Can you explain how is there a positive expectation when you follow basic strategy and have a total of ten against a dealer 10 or ace showing (no dealer blackjack). Your table shows a positive expectation for both these scenarios, but I can’t understand how. I would think under this scenario the player and dealer follow the same strategy, that is to hit until 17 or better or bust. The soft 17 is eliminated for the player under this scenario so I can’t understand where the positive expectation comes from.
— Srikanth

Thanks for the kind words. Let’s assume six decks (it doesn’t matter whether the dealer hits or stands on soft 17). My blackjack appendix 9 shows the expected value of 6+4 against an ace to be +0.081336, and 6+4 against a 10 to be +0.026796. The reason the expected values are positive is my expected value tables assume the dealer already has peeked for a blackjack and has confirmed that he doesn’t have one. Meanwhile the player can still draw an ace for a 21. In other words the player can make 21 on his next card and the dealer can not by assumption. If I had such a table under the European no peek rule the expected values would indeed be negative.

On my recent visit in Vegas I saw two dealers independent from each others (one at The Orleans, one at Circus-Circus) suggest to double on 4-4 vs. 6 instead of split. I was the BJ guy of our group and so my friends started to ask me about that. All I could say was: no, splitting is the right decision. (Of course provided that double after split is allowed.) Can I find out the probabilities of these alternatives or can you tell me? kind regards
— Werner

I’ve said this before but as much as I respect dealers as a group they give out a lot of bad advice and misinformation. Splitting fours against a five or six is a frequent play where both players and dealers incorrectly rebuke splitting. Sometimes you hear people say falsely that you should never split "anything that starts with F", in other words fours, fives, and faces. That is true about fives and faces but the player should indeed split fours against a five or six if double after split is allowed. Otherwise the player should hit, except in single deck he should double if allowed. My blackjack appendix 9 shows in a six-deck game where the dealer hits a soft 17 the following expected values of 4,4 against a 6.
Stand: -0.114085
Hit: + 0.113365
Double: + 0.092929
Split: +0.207228 (double after split allowed)
Split: + 0.056954 (double after split not allowed)

Wizard, I have been reviewing your site in preparation for a trip to Vegas, because it is the best gambling site period. I was intrigued by the analysis from your December 4, 2001 column about when to stand with 16 vs. dealer 10. Being a math person myself I want to maximize the odds, but also understand the slim gain. Like many basic strategy players, I’ve always hit 16 vs. dealer 10 when I hold a 2, 3, 4, or 5. I’m curious, since this was brought to your attention, have you altered your play to gain that "one unit every 5 years", or have you stuck with just hitting the 16 every time? Thanks for all you do!
— Anonymous

Thanks for the kind words. If I’m playing basic strategy (as opposed to counting) I tend to stand if there is already a four or five in my hand. If it is a face-up game, with other players, I scan the table and just use my best judgment.

In blackjack where the dealer exposes both cards (appendix 16), a pair of 8’s is not split against the dealer’s total of 10 or 11; instead, it says hit against the 10 and stand against the 11. Why is this different from regular BS where we split 8’s against the dealer’s ten or ace?
— David from Fort Wayne, IN

In regular blackjack the player should indeed split eight’s against a dealer 10 or ace up. However if the dealer accidentally flipped over both his cards, showing a total of 10 or 11, the player should hit against a 10 and stand against an 11. The reason is that when the dealer has a ten or an ace up, by the time it’s your turn you know the dealer does not have blackjack, because he peeked at the hole card to make sure. So you can play your hand more aggressively. But when both dealer’s cards are exposed to show a total of ten or eleven, then the dealer can certainly draw an ace to the ten, or a ten to the eleven, for a total of 21, so in that case you should proceed more conservatively.

In Effect of Card Removal in Blackjack you have the effect of removing a 6 less than a 5 or 4....is this correct? (i thought 6’s were the best or very close to 5’s for the best for being removed). Thanks
— David from Atlantic City, NJ

I think you are confusing card removal with the dealer’s up card. The following table shows the player’s expected value according only to the dealer’s up card, before the dealer checks for blackjack, assuming the dealer stands on soft 17 and infinite decks.

Expected Value by Dealer Up Card
Up Card Expected
Value
2 9.10%
3 12.38%
4 15.85%
5 19.65%
6 23.40%
7 14.40%
8 5.82%
9 -4.06%
10 -17.36%
A -33.78%
So it is indeed true that if you could choose an up card for the dealer it should be a six. While sixes are bad for the dealer they are bad for the player as well. All things considered, if you could remove one card from the shoe you should choose a five.

Great site! Your blackjack strategy card is the best one I’ve seen. Is it available any where? Theone I’m currently using does’t have surrender on it, what am I loosing by using this?
— John C from Crestwood

Thanks. Almost every casino gift shop sells basic strategy cards, but for some reason they don’t indicate when to surrender. There are not many situations to surrender, but those situations happen often, so I think they are worth memorizing. In a six-deck game surrender is worth 0.07% if the dealer stands on soft 17, and 0.09% if he hits it.

My friend I were playing in LV. We had a big argument on what has statistically better odds, double down with player totaling 10 versus dealer showing 7, or double down with player totaling 11 versus dealer showing 10, in a two deck game. I thought it was the prior.
— Brett from Alhambra

My blackjack appendix 9 was created for just these kinds of questions. Assuming 6 decks, my table shows the expected value of doubling 8+2 vs. 7 is 0.396342. The expected value of doubling 8+3 vs. 10 is 0.176919. So you are right, 10 vs. 7 is the much better hand to have.

According to standard BJ rules and perfect basic strategy, how many percent of my DOUBLED DOWN hands should I expect to win, push and lose?
— Cameron from Melbourne, Australia

Assuming liberal Vegas Strip rules (six decks, dealer stands on soft 17, double after split allowed, late surrender allowed, resplitting aces allowed) the following are the probabilities of each possible outcome when doubling on the initial two cards. This does not include doubling after splitting.

Win: 54.99%
Lose: 38.06%
Draw: 6.95%

I have a friend who starts complaining when his first card is a six, without waiting to see what his second card and the dealer’s up card are. I think he should wait because he could get a two, three, four, five, etc. (i.e., a decent second card) OR the dealer could show a two through six (a good card for the table). What do you think? How much worse are his odds of winning with a first card of six without knowing this second card or the dealer’s up card? Or is my friend just a whiner? Thank you for your time.
— Scott from Long Beach

My blackjack appendix 14 shows that if your first card is a six your expected value is already about −21%. For example, if he bet $100, a fair price to sell the hand and bet would be about $79. Maybe you can take advantage of his complaining by offering to buy his hand for less than the fair 79 cents on the dollar. I’d suggest 75 cents on the dollar, to give you an edge, without taking too much advantage.

I had a situation playing blackjack last weekend, where the dealer had a 6 on top but when he was tucking in the down card he accidentally showed that he had a 3 in the hole. The player on my right had a 15, I had an 11, and the player on my left had a 12. Knowing that the dealer had a total hand of 9, the player on my right hit his hand and busted with a 10. I wound up doubling down and got a 2. The player on the left hit his hand getting a 5, for a total of 17. The dealer opened his hand of 9 and hit a ten for a total of 19. The dealer told us even though you saw the 3 under that you should play your hand as if you did not know the down card. I wanted to ask you what you would have done in the situation for all three players. This is the first time that has ever happened since I have been playing blackjack. Please advise. Thanks!
— Larry C. from Daly City

My flashing blackjack dealer strategy shows what to do in any situation where the dealer accidentally exposes his hole card. However, most players don’t have that memorized, incluing me. In cases like this where the dealer’s two cards total nine or less you may use basic strategy, assuming the dealer’s up card is the sum of his two cards. Using that rule of thumb, all three players played correctly. Contrary to what the dealer said, the player has every right to use any information gleaned from dealer errors like this. Not only would I have ignored the dealer’s comment, I would have kept playing, hoping he would do it again.

Thanks for creating a great site, with such detailed information. You stated a significant decrease in house edge for the various Charlies in blackjack, but I didn’t see any suggestions on playing differently. Are there any basic strategy exceptions that are worth making to maximize profit in a large (6+ decks) shoe? I assume you would hit more if you were one card away from a Charlie against an ace, since it is so unlikely for the dealer to bust, but I would love to see specific instructions. Thanks.
— Matt N. from Ann Arbor

You’re welcome. For those readers who may not understand the question, a "Charlie" is a rule in which the player automatically wins if he hits to some number of cards, usually five to seven, without busting. The following table, for three or more cards, shows the basic strategy if the player is one or two cards away from such an automtic winner.

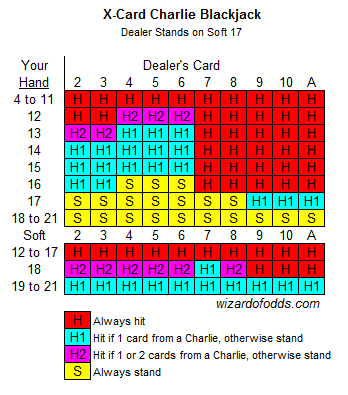
Many casinos allow bets behind another player’s on the blackjack table. Can you please tell us the proper pair-splitting strategy when the "behind" wager far exceeds the regular wager, assuming the two bettors are working together?
— Jim from Brick, NJ

I hope you’re happy, I added a new page to answer this question. Please see my Blackjack Appendix 19.

I have studied and used your blackjack appendix 16 (dealer exposes hole-card strategy) for some time now, and there is still one play that I can not find a mathematical explanation for: A2 vs. 5. Basic strategy would have this as a double, and using your own "effect of card removal" numbers, removing a 2 & 3 from the deck when you have a soft 13 should make the deck favor the player MORE, not less. What am I not seeing?
— Rodger from Phelpston ON

The reason is my blackjack basic strategy is based on 8 or fewer decks, and the flashing dealer strategy is based on an infinite number of decks. In an infinite-deck blackjack game you should hit A2 vs. 5 as well. An infinite-deck assumption is the lazy way to analyze blackjack. The reason I went that way is I believe that is not a frequently used page, and the cost in errors is very small, only one unit for every 202,000 units bet.

I think I noticed an error in your splitting strategy with a back-betting player for blackjack. It states that you should only play one hand if the person you are back-betting splits 10s vs. 8 (this is the selfish chart). But a hard 10 (no double) vs. 8 still has a positive expected value.
— Mason from D.C.

The reason is that my table assumes the front-player will keep resplitting, if he can. That depresses the value of a single 10, because I assume the front-player will keep making the same mistake, if he can. I just added that condition to that page.

Thank you for your detailed site. In blackjack appendix #9 you state the expected value for the game and the expected value for each play. I would expect the expected value for the game would be the sum of E_i × P_i where E_i is the maximum expected value for the i^th play (stand/hit/double/split) and P_i is the probability for the i^th play. When I try this calculation I get a different result. For example, six decks, dealer hits on soft 17, and player may not double after split I get 0.04518876.
— Frank from San Diego

Those tables assume the dealer does not have a blackjack. This is because by the time it is the player’s turn to act, the dealer has already peeked for blackjack. Making correct double and split decisions should be based on the conditional expected value, given the dealer does not have a blackjack. Otherwise, the player would be overly timid about doubling or splitting against a ten or ace. Adding up the dot product of probabilities and expected values will give an incorrect result, because there is no loss represented for a dealer blackjack.
To get the house edge of the overall game you should subtract the expected loss when the dealer has a blackjack. With six decks, the probability of a dealer blackjack is the number of tens, times number of aces, divided by the number of two-card combinations, which is (6×16)×(6×4)/combin(312,2) = 0.047489. However, the player will only lose when he does not have a blackjack. The probability of a player blackjack, given that the dealer already has one, is (6×16-1)×(6×4-1)/combin(310,2) = 0.045621. So, the probability of the player losing to a dealer blackjack is 0.047489 × (1-0.045621) = 0.045323. You should subtract this number from your dot product above: 0.04518876 - 0.045323 = -0.00615144. Thus, the house edge under the rules stated in the appendix is 0.62%.

I follow your 4+ deck Blackjack basic strategy 100% of the time and I always get dirty looks whenever I hit my 12 against a dealer 2 and especially a 3. I don’t know how to explain to the other players in simple terms why what I’m doing in the best thing to do.
— Everett from St. Charles, MO

I feel your pain. You can imagine how bad it gets in Spanish 21, which calls for such plays as hitting 14 against a 3. As long as it is just looks, I would let it slide. If it gets to words, I would say something like, "There are lots of other tables in here." There is no way you are going to convince simpletons like this by trying to explain the odds. The more ridiculous a belief is, the more tenaciously it tends to be held.
There is usually no sound-bite explanation anyway to why one play is better than another. To know why the correct play is what it is, one must either consider every possible way the remaining cards could fall, for both player and dealer, or play out the hand thousands of times, even millions for very borderline hands. The decision with the highest expected value is the one you should take. Only refusing insurance yields itself to being easily explained.

I know what the chart says, but I can’t make myself split eights against a dealer 9, 10 or ace in blackjack. My question is what is this doing to the house edge?
— boomdog

Let’s assume six decks, the dealer stands on soft 17, and the player may re-split to up to four hands. The effect of each basic strategy change is the probability of the hand’s occurring and the cost of not making the correct play when it does. My blackjack appendix 9 shows both the probability of each hand and the expected value of each play. Assuming the player chooses to hit instead of split, the effect on the expected value of the game is:
Prob(8,8 vs A)×(EV(hit)-EV(split)) + Prob(8,8 vs 9)×(EV(hit)-EV(split)) + Prob(8,8 vs 10)×(EV(hit)-EV(split))
= 0.0003036 × (-0.513551 -(-0.364371)) + 0.0004404 × (-0.505707 -(-0.38995)) + 0.0016249 × (0.535361 -(-0. 475385))
= -0.019%.
So hitting 8,8 against a dealer 9, 10 or ace increases the house edge by 0.019%, or about one bet every 5,300 hands played. If the player surrenders instead of hitting, the effect drops to 0.013%. So, it is not a significant mistake. To put it in comparison, taking "even money" with a blackjack against a dealer ace increases the house edge by 0.014% in a six-deck game. If the player insures every blackjack and 20 (a common mistake), then the error cost jumps to 0.149%!
This question was raised and discussed in the forum of my companion site Wizard of Vegas .

I was playing 6-5 blackjack at a Strip casino a while back and had consumed just enough free booze that I doubled every time I got a blackjack against a dealer 2-6. Fortunately, I won every time. But, I wonder how bad my decision was. Would it make sense if blackjack paid even money?
— Jumboshrimps

My blackjack appendix 9 is useful to answer questions like this. For example, assuming six decks and the dealer hits a soft 17, the expected value of doubling on a blackjack against a dealer 5 is 0.622136 and against a 6 is 0.667063. Both are much less than 1.2, costing over half a bet. Even if a blackjack only pays even money, as is unfortunately sometimes the case now, you should stand on the blackjack. The only game where you should not stand on a blackjack is in Triple Up 21, where the player should triple on a blackjack against a dealer 6.
This question was raised and discussed in the forum of my companion site Wizard of Vegas .

Your blackjack basic strategy tables are based on maximizing the expected value per hand. However, are there situations where doubling or splitting is such a marginally bad play compared to hitting or standing that the cost of the error is less than the house edge of playing an additional hand?
— jburgess

Yes! Let’s consider the following situation:
6 decks
Dealer hits soft 17
Player has A,6
Dealer shows 2
According to my blackjack appendix 9, the following is the expected value of each play:
Stand -0.152739
Hit -0.000274
Double -0.004882
So, hitting is the play that results in losing the least amount of money on average for that hand. If the player were to double, the expected value of that error would be -0.004882 - (-0.000274) = -0.004608. According to my blackjack house edge calculator, the house edge under those rules — assuming surrender, double after a split and re-splitting aces — is 0.48%. Usually, some of those options won’t be allowed, increasing the house edge. So, as long as the dealer hits a soft 17 in a 6-deck game, the cost of doubling soft 17 against a 2 is less than the cost of betting the same amount on an additional hand.
You could make your same point in any game that involves raising. For example in Three Card Poker, if you want to minimize the expected loss per hand, then the optimal strategy is to raise on Q64 or better, as I state on my Three Card Poker page. However, if your goal is to minimize the expected loss per total amount bet, then the optimal strategy is to raise on Q62 or better.
This begs the question of why do gambling writers like me base strategy on minimizing the expected loss per original bet, rather than the total amount bet? My answer is that it is mainly out of tradition. That is how the blackjack basic strategy was created, and everybody has kept that methodology out of habit and simplicity. If the recreational player’s goal is to minimize losses over a defined period of time, then he should go with conventional strategies that minimize the expected loss per hand. If the player’s goal is to minimize losses over $x in total bets, then he should make the kind of marginally bad doubles and raises mentioned. I tend to think most players have a time-based goal, favoring the conventional strategies.
This question was raised and discussed in the forum of my companion site Wizard of Vegas .

I know a lot of blackjack players don’t like to split eights against a 9, 10 or ace. Do you think that play is the one most frequently played incorrectly? If not, what do you think is?
— Kellynbnf

The play that I think has the highest probability of being played incorrectly by blackjack players is splitting 4,4 against a 5 or 6 when double after split is allowed. The probability of getting one or the other situation in a six-deck game is 1 in 1135. According to my blackjack appendix 9 , assuming the player hits instead of splitting, the cost in expected value is 2.83% against a 5 and 4.38% against a 6. Overall, the house edge of the game goes up by 0.0032% when the player habitually makes this mistake every time it occurs. So, it isn’t a very costly error, because it happens so infrequently. However, I don’t think I’ve ever seen another player correctly split in this situation. When I do, the dealers and other players usually roll their eyes. Once I heard another player incorrectly say to the dealer, as if I wasn’t there, "You should never split any hand that starts with an F."
If the question were what is the most costly mistake, considering both the frequency of the play and cost of the error, then I can only hazard a guess. That guess would be that the #1 error is not soft doubling when you are supposed to. Seldom do I see recreational players double a hand like soft 17 against a 6. The following table shows the increase in the house edge as a result of four commonly made mistakes. This table assumes the player always makes the error when the situation occurs, instead taking the second best option. For standing on 12 against a 2 or 3 I did not include a player 6,6.

Frequent Blackjack Errors

Error Probability Avg. Cost per Incident Cost per Hand

Never soft double 0.016430 0.054357 0.000893

Stand on 12 against 2 or 3 0.000380 0.029955 0.000380

Stand on soft 18 against 9-A 0.000205 0.041605 0.000205

Hit 8,8 against 9-A 0.000194 0.081779 0.000194

This question was raised and discussed in the forum of my companion site Wizard of Vegas .

Why is it that the basic strategy says to hit on 16 vs. 10, while the Hi-Lo count says to stand on a count greater than or equal to zero? Isn't the basic strategy based on a full shoe, thus with a count of zero? It would seem both can't be right.
— Anonymous

First, it bears repeating that 16 vs. 10 is an extremely borderline hand between hit and stand. If you're allowed to surrender, that is much better than either hitting or standing for the basic strategy player. Otherwise, hitting is a tiny bit better, on average. It would take the removal of just one small card from an eight-deck shoe to sway the odds in favor of standing, because with one fewer small card there are more large cards left, making hitting more dangerous. That is why I say that if your 16 is composed of three or more cards you should stand, because a 3-card 16 has usually removed at least two small cards from the shoe.

Second, on the first hand after a shuffle, if the basic strategy and a card counting strategy differ on how to play the hand, then the basic strategy prevails. The basic strategy was carefully created to consider the exact deck composition based on the specific cards observed. A table of index values is a blunter instrument that is applicable throughout the shoe.

In this particular case a card counter could either hit or stand, depending on how he rounds the true count. If he rounds down, the true count will be -1, causing him to hit. If he rounds up, or to the nearest integer, the true count will be 0, causing him to stand. As long as I bring this up, according to Blackjack Attack by Don Schlesinger, the methodology of choice for rounding is "flooring," or rounding down, in this case to -1, causing the player to correctly hit.

Another similar situation is 15 vs. 10. 83% of the time (with a 10+5 or 8+7, but not 9+6), this results in a running count of -1 the first hand after a shuffle, and the index number to surrender is 0. Rounding down would cause the player to incorrectly hit, when surrendering is better.

The bottom line is that for the first decision after a shuffle, with no other cards known from other players, the card counter should use basic strategy. After that, resume using index numbers.

This question was raised and discussed in the forum of my companion site Wizard of Vegas .

Ask the Wizard: Blackjack - Basic Strategy (Specific Hands)

In your Blackjack strategy you surrender 16 against A,10,9. You say to split a pair of 8’s against those cards. I have been told that a pair of 8’s is a 16 and should be surrendered. What do you think? — Jim from Naples, Florida

If the dealer checks his hole card, and does not have blackjack,why hit a soft 18 against an ace; also, why not double on an 11? — Randy from Columbus, Ohio

Hi there - love your site! If I have blackjack, and the dealer is showing an ace, I am given the option of taking even money or continuing the hand. Should I take the even money or play on? — Ross from New York, New York

Mike, On my last trip to Vegas, a dealer I’ve come to know said he was "toying with the idea" of standing on a 16 against a dealer’s 7 because only 5 of the 8 cards give the dealer an automatic win. How does this strategy play out? — Chris from Gaithersburg, Maryland

Regarding your exceptions to surrender in appendix six, how should I best adapt it to the Unified Gaming single-deck game with early surrender against the ace? Thanks for any help and great site. — Dave from Provo, USA

I just came back from Costa Rica. They pay even money on a blackjack. What is this worth to the house and should I double down on 21 versus say a dealer 3-6, since I am only going to get paid 1to1? — Rick from Jacksonville, USA

Hi, I just looked at your Microgaming blackjack basic strategy card. I notice that on 7,7 you advise that the player not hit against a 10. Why is this, and does this override the advice to hit on 14 against a 10? — Joseph Teo from Singapore

If you have 15 and the dealer shows an eight...basic strategy say to hit. In this case, whether you hit or stay your chance of losing is over 70%........why is not the better play to surrender if you are going to lose over 70% of the time no matter if you hit or stay? — Nino from Glastonbury, USA

If the dealer does not check for blackjack with a ten showing, instead taking only the original wager at the end of the hand, does that necessitate any strategy changes? — Anonymous

You make a good mathematical argument that the player should refuse insurance. However you don’t make a good psychological argument. Most people would feel like a fool giving up a bird in the hand to lose a shot at 1.5 birds in the bush. — Anonymous

Why does your Blackjack Switch basic strategy table say to always hit on 12? — Anonymous

My wife knows blackjack basic strategy but insists on being a ’hunch’ player. What are the hands that are closest to 50-50 so that my wife can limit her hunch plays to those? — Anonymous

I looked up and down on your blackjack section and can’t find out "how" to surrender. I know what it is and all, but do I just grab half my chips and that’s that? — Anonymous

Why do you say not to double on 10 or 11 against a 9 in Blackjack Switch? — Anonymous

I heard the other day that if you’re playing a 6:5 game (or the even money game at Rio), you should double down when dealt a natural to help offset the lower payout. Is this correct? What would the expected loss be for that play? — Anonymous

Are there any basic strategy exceptions for doubling and splitting on the Internet when cash back applies to the total amount bet (thus giving the player an extra incentive to double or split). Please assume a cash back rate of 0.1%. — Anonymous

In blackjack the strategy for 16 vs. 10 is R,S since once you eliminate the 2-card hands the strategy is stand (not hit) for any number of decks. — Anonymous

The index number of 16 against a 10 in most blackjack counting systems is zero. So if the deck were completely neutral you should stand, because you stand if the count is equal or exceeds the index number. Yet the basic strategy tables tell us to hit. This seems to be a contradiction. — Anonymous

Sometimes the dealer exposes his hole card in blackjack. What is the correct basic strategy when that happens? — Anonymous

Should I use your basic strategy exceptions after splitting? — Mick

In Effect of Card Removal in Blackjack you have the effect of removing a 6 less than a 5 or 4....is this correct? (i thought 6’s were the best or very close to 5’s for the best for being removed). Thanks — David from Atlantic City, NJ

Great site! Your blackjack strategy card is the best one I’ve seen. Is it available any where? Theone I’m currently using does’t have surrender on it, what am I loosing by using this? — John C from Crestwood

My friend I were playing in LV. We had a big argument on what has statistically better odds, double down with player totaling 10 versus dealer showing 7, or double down with player totaling 11 versus dealer showing 10, in a two deck game. I thought it was the prior. — Brett from Alhambra

According to standard BJ rules and perfect basic strategy, how many percent of my DOUBLED DOWN hands should I expect to win, push and lose? — Cameron from Melbourne, Australia

Many casinos allow bets behind another player’s on the blackjack table. Can you please tell us the proper pair-splitting strategy when the "behind" wager far exceeds the regular wager, assuming the two bettors are working together? — Jim from Brick, NJ

I follow your 4+ deck Blackjack basic strategy 100% of the time and I always get dirty looks whenever I hit my 12 against a dealer 2 and especially a 3. I don’t know how to explain to the other players in simple terms why what I’m doing in the best thing to do. — Everett from St. Charles, MO

I know what the chart says, but I can’t make myself split eights against a dealer 9, 10 or ace in blackjack. My question is what is this doing to the house edge? — boomdog

I know a lot of blackjack players don’t like to split eights against a 9, 10 or ace. Do you think that play is the one most frequently played incorrectly? If not, what do you think is? — Kellynbnf

Why is it that the basic strategy says to hit on 16 vs. 10, while the Hi-Lo count says to stand on a count greater than or equal to zero? Isn't the basic strategy based on a full shoe, thus with a count of zero? It would seem both can't be right. — Anonymous

In your Blackjack strategy you surrender 16 against A,10,9. You say to split a pair of 8’s against those cards. I have been told that a pair of 8’s is a 16 and should be surrendered. What do you think?
— Jim from Naples, Florida

If the dealer checks his hole card, and does not have blackjack,why hit a soft 18 against an ace; also, why not double on an 11?
— Randy from Columbus, Ohio

Hi there - love your site! If I have blackjack, and the dealer is showing an ace, I am given the option of taking even money or continuing the hand. Should I take the even money or play on?
— Ross from New York, New York

Mike, On my last trip to Vegas, a dealer I’ve come to know said he was "toying with the idea" of standing on a 16 against a dealer’s 7 because only 5 of the 8 cards give the dealer an automatic win. How does this strategy play out?
— Chris from Gaithersburg, Maryland

Regarding your exceptions to surrender in appendix six, how should I best adapt it to the Unified Gaming single-deck game with early surrender against the ace? Thanks for any help and great site.
— Dave from Provo, USA

I just came back from Costa Rica. They pay even money on a blackjack. What is this worth to the house and should I double down on 21 versus say a dealer 3-6, since I am only going to get paid 1to1?
— Rick from Jacksonville, USA

Hi, I just looked at your Microgaming blackjack basic strategy card. I notice that on 7,7 you advise that the player not hit against a 10. Why is this, and does this override the advice to hit on 14 against a 10?
— Joseph Teo from Singapore

If you have 15 and the dealer shows an eight...basic strategy say to hit. In this case, whether you hit or stay your chance of losing is over 70%........why is not the better play to surrender if you are going to lose over 70% of the time no matter if you hit or stay?
— Nino from Glastonbury, USA

If the dealer does not check for blackjack with a ten showing, instead taking only the original wager at the end of the hand, does that necessitate any strategy changes?
— Anonymous

You make a good mathematical argument that the player should refuse insurance. However you don’t make a good psychological argument. Most people would feel like a fool giving up a bird in the hand to lose a shot at 1.5 birds in the bush.
— Anonymous

Why does your Blackjack Switch basic strategy table say to always hit on 12?
— Anonymous

My wife knows blackjack basic strategy but insists on being a ’hunch’ player. What are the hands that are closest to 50-50 so that my wife can limit her hunch plays to those?
— Anonymous

I looked up and down on your blackjack section and can’t find out "how" to surrender. I know what it is and all, but do I just grab half my chips and that’s that?
— Anonymous

Why do you say not to double on 10 or 11 against a 9 in Blackjack Switch?
— Anonymous

I heard the other day that if you’re playing a 6:5 game (or the even money game at Rio), you should double down when dealt a natural to help offset the lower payout. Is this correct? What would the expected loss be for that play?
— Anonymous

Are there any basic strategy exceptions for doubling and splitting on the Internet when cash back applies to the total amount bet (thus giving the player an extra incentive to double or split). Please assume a cash back rate of 0.1%.
— Anonymous

In blackjack the strategy for 16 vs. 10 is R,S since once you eliminate the 2-card hands the strategy is stand (not hit) for any number of decks.
— Anonymous

The index number of 16 against a 10 in most blackjack counting systems is zero. So if the deck were completely neutral you should stand, because you stand if the count is equal or exceeds the index number. Yet the basic strategy tables tell us to hit. This seems to be a contradiction.
— Anonymous

Sometimes the dealer exposes his hole card in blackjack. What is the correct basic strategy when that happens?
— Anonymous

Should I use your basic strategy exceptions after splitting?
— Mick

In Effect of Card Removal in Blackjack you have the effect of removing a 6 less than a 5 or 4....is this correct? (i thought 6’s were the best or very close to 5’s for the best for being removed). Thanks
— David from Atlantic City, NJ

Great site! Your blackjack strategy card is the best one I’ve seen. Is it available any where? Theone I’m currently using does’t have surrender on it, what am I loosing by using this?
— John C from Crestwood

My friend I were playing in LV. We had a big argument on what has statistically better odds, double down with player totaling 10 versus dealer showing 7, or double down with player totaling 11 versus dealer showing 10, in a two deck game. I thought it was the prior.
— Brett from Alhambra

According to standard BJ rules and perfect basic strategy, how many percent of my DOUBLED DOWN hands should I expect to win, push and lose?
— Cameron from Melbourne, Australia

Many casinos allow bets behind another player’s on the blackjack table. Can you please tell us the proper pair-splitting strategy when the "behind" wager far exceeds the regular wager, assuming the two bettors are working together?
— Jim from Brick, NJ

I follow your 4+ deck Blackjack basic strategy 100% of the time and I always get dirty looks whenever I hit my 12 against a dealer 2 and especially a 3. I don’t know how to explain to the other players in simple terms why what I’m doing in the best thing to do.
— Everett from St. Charles, MO

I know what the chart says, but I can’t make myself split eights against a dealer 9, 10 or ace in blackjack. My question is what is this doing to the house edge?
— boomdog

I know a lot of blackjack players don’t like to split eights against a 9, 10 or ace. Do you think that play is the one most frequently played incorrectly? If not, what do you think is?
— Kellynbnf

Why is it that the basic strategy says to hit on 16 vs. 10, while the Hi-Lo count says to stand on a count greater than or equal to zero? Isn't the basic strategy based on a full shoe, thus with a count of zero? It would seem both can't be right.
— Anonymous