Wizard Recommends Cards

Ask The Wizard #407

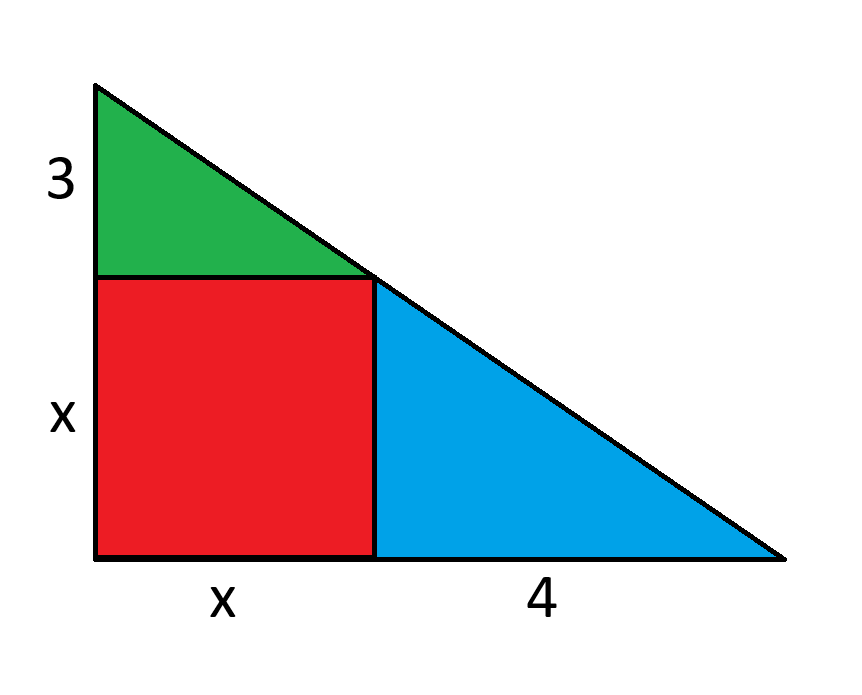
Find x.

anonymous

Let's set up a equation matching the area of the individual parts to the entire triangle:

Green + Blue + Red = Total
3x/2 + 4x/2 + x^2 = (x+3)*(x+4)/2
3x + 4x + 2x^2 = (x+3)*(x+4)
7x + 2x^2 = x^2 + 7x + 12
2x^2 = x^2 + 12 x^2 = 12 x = 2*sqrt(3) =~ 3.464102

This question is based on a similar one by Presh Talkwalkar of the "Mind Your Decisions" YouTube channel, specifically the first problem in this video. Presh presents a clever and different solution than mine.

You are at an oasis in the desert. It is your task to deliver a letter 100 miles away as quickly as possible. Your camel can carry up to a three-day supply of water and can travel 20 miles per day. Leaving caches of water in the desert is allowed. What is the fastest you can deliver the letter?

anonymous

Clicking the following button will reveal my answer. It shows my fastest time, but I can't prove there isn't a better way.

11.8 days

 

  1. Make four trips to an outpost 8 miles away. You will be able to cache 44 gallons on the first three trips and add 52 on the fourth, for a total of 184 gallons delivered. This will entail 7*8=56 miles of walking, which will take 56/20 = 2.8 days.
  2. Make three trips to an outpost 12 miles away. You will be able to cache 36 gallons on the first two trips and add 48 on the third, for a total of 120 gallons delivered. This will entail 5*12=60 miles of walking, which will take 60/20 = 3.0 days.
  3. Make two trips to an outpost 20 miles away. You will be able to cache 20 gallons on the first trip and add 40 on the second, for a total of 60 gallons delivered. This will entail 3*20=60 miles of walking, which will take 60/20 = 3.0 days.
  4. Make one trip to an outpost 60 miles away. This will entail 60 miles of walking, which will take 60/20 = 3.0 days.

The distance to the outpost is 8+12+20+60 = 100 miles. Total time required is 2.8 + 3.0 + 3.0 + 3.0 = 11.8 days.

You have a martini glass that is 4" high. How high should you fill it to serve half of a full portion?

anonymous

4×(1/2)^(1/3) = 3.174802" high.

 

Interestingly, it doesn't matter what the radius is. Let's call the radius r. Let's call the height the bartender should fill the glass h. It is obvious the radius of the half portion is the same ratio as that of the two heights. In other words, the radius of the half portion is r*(h/4).

Recall the volume of a cone is (1/3)*h*pi*r2.

Let's equate the half portion to half of a full portion:

(1/2)*(1/3)*4*pi*r2 = (1/3)*h*pi*(rh/4)2

(1/2)*4*r2 = h*(rh/4)2

2*r2 = h*r2*h2/16

2 = h3/16

32 = h3

h = 321/3 =~ 3.174802"