Ask The Wizard #399
If you take out the small square from the first image and rearrange the pieces the total area still seems to be the same. How is this possible?
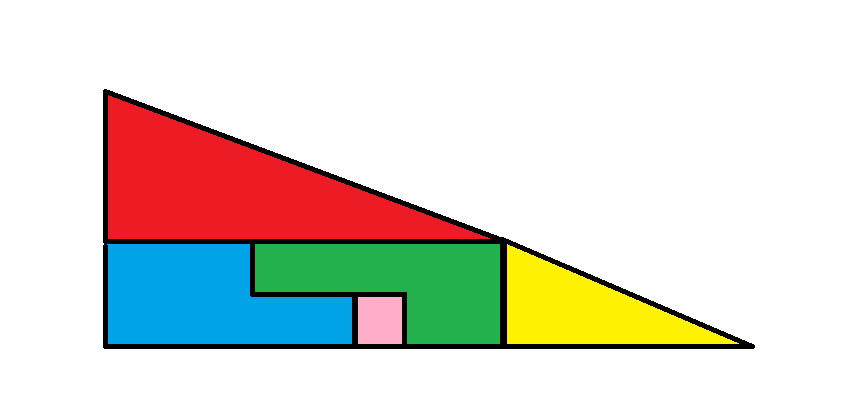
Image 1
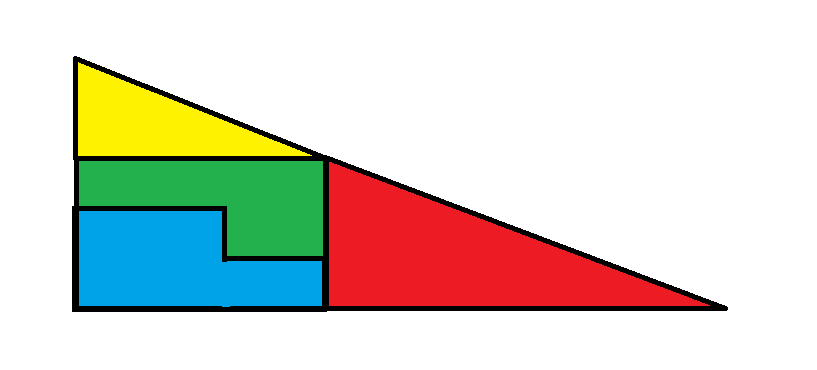
Image 2
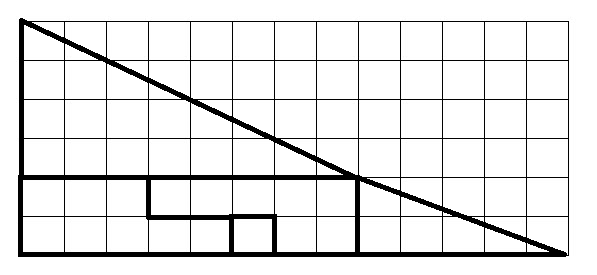
The image above shows the first image on a grid, to better see the size of each piece.
Note that the large red triangle has sides of length 4 and 8. Next note that the smaller yellow triangle has sides of length 2 and 5. In other words, the triangles are not proportional. The hypotenuse of the two triangles do not have the same slope as placed in either figure. One has slope 0.5 and the other 0.4. Placing the pieces the way they are in either figure makes it look like they form a large triangle of sides 5 and 13, but it isn't a triangle.
The area of the red triangle is 4*8/2 = 16.
The area of the yellow triangle is 2*5/2 = 5.
In the first image, the other three pieces form a rectangle of size 2 by 8, for a total area of 16.
In the second image, the other two pieces form a rectangle of size 3 by 5, for a total area of 15.
The total area of the first image is red triangle + yellow triangle + big rectangle = 16 + 5 + 16 = 37.
The total area of the second image is red triangle + yellow triangle + small rectangle = 16 + 5 + 15 = 36.
To conclude, the first image is bigger with the small square. It's an optical illusion that the total pieces combined form a large triangle in both cases. They don't.
There are 16 motorcycles at the edge of a large desert. Each motorcycle can travel 100 miles on a tank of gas. All motorcycles start out with a full tank. Transferring gas between motorcycles is allowed. The goal is to get one motorcycle as far from the point of origin as possible. How far can it get?
The key to the problem is for the group to travel out a short way. Then take the remaining gas from one of the motorcycles and top off the tanks of the other ones.
For example, at the beginning divide a full tank of gas into 16 parts, one for each motorcycle. Then everyone drive together until 1/16 of a tank is consumed, which will get the group 100/16 = 6.25 miles. Take the 15/16 of a tank from one motorcycle and syphon 1/16 of a tank into the other 15 motorcycles, which will exactly top them off.
Then repeat the same process, but with 15 motorcycles left, travel as far as 1/15 of a tank will take you, which is 100/15 = 6.666667 miles. Then take one other 14/15 of a tank from one motorcycle and syphon 1/15 of a tank to the other 14 motorcycles.
Continuing in this process will get the last motorcycle a total distance of (1/16) + (1/15) + (1/14) + ... + (1/1) =~ 338.072899 miles.
This question was asked and discussed in my forum at Wizard of Vegas.
What are your thoughts on the Sleeping Beauty Paradox?
For the benefit of other readers, here is what is being asked in the Sleeping Beauty Problem/Paradox.
Sleeping Beauty (SB) volunteers for an experiment. All the details of the experiment are truthfully explained to her, as follows:
- Sunday: SB is put to sleep. After she falls a asleep a fair coin will be flipped.
- Monday: SB will be wakened on Monday and asked "What is the probability the coin landed on heads?" After she replies she will be put back to sleep with an amnesia drug that will cause her to forget everything that happened on Monday.
- Tuesday: If the coin landed on tails, the same thing that happened on Monday will happen again. If the coin landed on heads, she sleeps through the entire day.
- Wednesday: SB is wakened again, asked nothing, and goes home as the experiment is over.
The question is how should she answer the question asked on Monday and perhaps on Tuesday?
My Answer
If this experiment were repeated million of times, we could expect to see three types of wakenings, each equally likely:
- Coin lands on heads, wakening on Monday.
- Coin lands on tails, wakening on Monday.
- Coin lands on tails, wakening on Tuesday.
This is because the wakenings are Monday should be equally divided between coin flips of heads and tails. Also, if the coin lands on tails, then the wakenings on Monday and Tuesday will be exactly equal. Thus, all three groups will have about the same number of wakenings over a large sample size.
Of those wakenings, one out of three occur after heads is flipped. Thus, the probability of the coin landed on heads is 1/3.
The 1/2 camp argues that SB is given no additional information upon each wakening and thus should assume each outcome of the flip was equally likely.
To that, I would extend the problem to 999,999 wakenings if the coin landed on tails. Only 1 in one million wakenings would happen after a heads is flipped. So, it would be pretty easy to assume upon any awakening it probably was one of the 999,999 wakenings after a tails. In other words, the correct answer in this case would be 1 in 1,000,000.
To offer another extension, what if SB were asked to predict the toss of the coin on each awakening. If she got it right, she would win $1,000. If she had a strategy to say “heads” she could expect to win (1/2)*$1,000 = $500. If had a strategy to say “tails” she could expect to win (1/2)*$2,000 = $1,000. So, just the fact that SB is awakened favors a the coin landing on tails.
If my explanation was not clear the Sleeping Beauty Problem at Wikipedia goes into it much deeper than I do, including other possible responses from SB.
This question was asked and discussed in my forum at Wizard of Vegas.




