Ask The Wizard #395
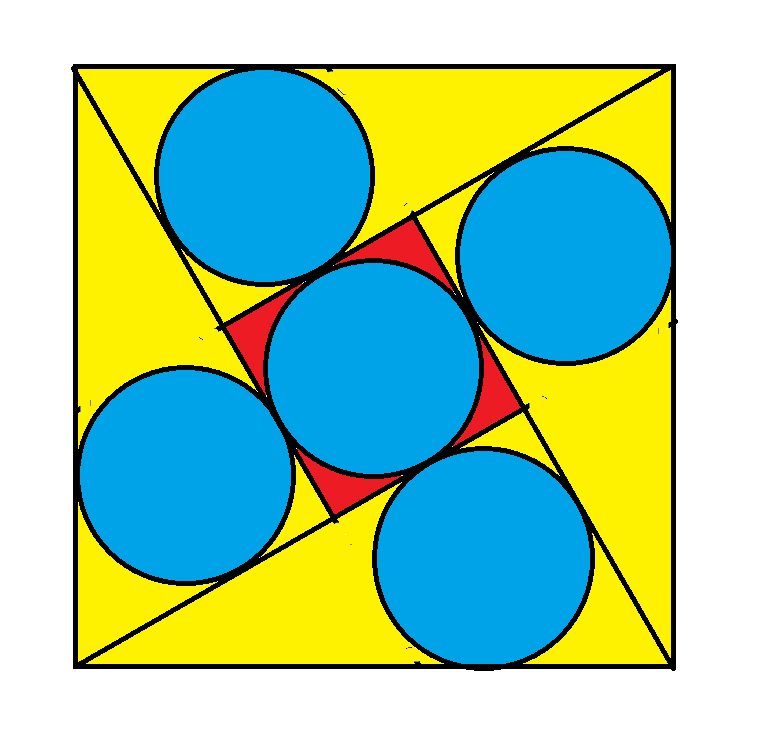
The diagram above consists of four right triangles and a small square inside a big square. The side length of the big square is 1. All five circles have the same diameter. What is that radius?
radius = (sqrt(3)-1)/4 =~ 0.183013.
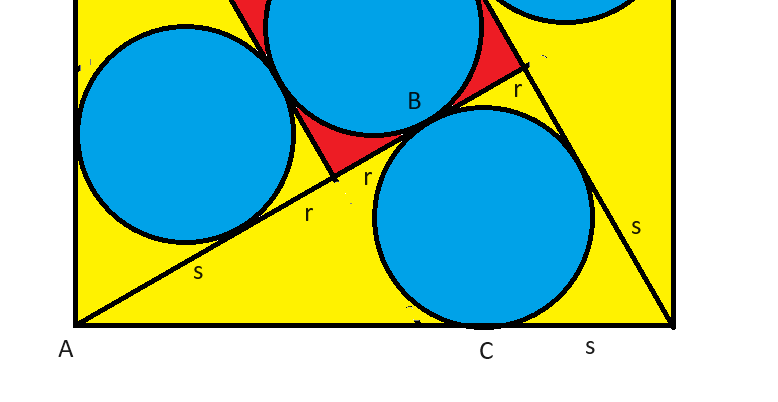
Let's consider one of the triangles. Let's define:
- r = Radius of the circles
- s = Distance between any corner of the big square and where the nearest circle is tangent to the triangle it is inscribed in.
Looking at the triangle in the image the distances are:
- short leg = r+s
- long leg = 3r+s
- hypotenuse = 1
Using the Pythagorean formula:
(r+s)2 + (3r+s)2 = 1
r2 + 2rs + s2 + 9r2 + 6rs + s2 = 1
10r2 + 2s2 + 8rs = 1
We need another equation to solve this. Let's look at the length of the big square, which we're given is 1. AB = AC. AB = 2r+s, so AC = 2r+s. The rest of the side of the big square is s. So:
2r + 2s = 1.
2s = 1-2r
s = 1/2 - r
Let's plug that into our equation from the Pytagorean formula:
10r2 + 2(1/2 - r)2 + 8r(1/2 - r) = 1
10r2 + 2(1/4 - r + r2) + 4r - 8r2 = 1
2r2 + 1/2 - 2r + 2r2 + 4r = 1
4r2 + 2r - 1/2 = 0
8r2 + 4r - 1 = 0
Using the quadratic equation:
r = (-4 +/- sqrt(48))/16
r = (sqrt(3)-1)/4 =~ 0.183013.
This problem was taken from the Mind Your Decisions YouTube channel. Presh offers a solution that doesn't require the Pythagorean formula.
This problem is asked and discussed in my forum at Wizard of Vegas.
What is your opinion of the "Right and Wrong Way System"? The way it works is the player makes a don't pass bet of one unit. If any point is rolled, the player bets one unit on that number. If the number hits, the player makes a profit and if he seven's out, he breaks even. This seems like a freeroll. What am I missing?
Let's generously say that if the point is a 4 or 10 the player pays the 5% commission on a win only. We will follow the Vegas rule where a 12 on the come out roll is a push on the don't pass bet (in northern Nevada they push on the 2). That said, here are all the possible outcomes:
- Come out roll of 2 or 3: Player wins one unit on don't pass bet.
- Come out roll of 12: Player pushes on don't pass bet.
- Come out roll of 7 or 11: Player loses on don't pass bet.
- Point of 4 or 10 and point wins: Player wins 1.95 units on buy bet and loses one unit on don't pass for net win of 0.95 units.
- Point of 5 or 9 and point wins: Player wins 1.4 units on place bet and loses one unit on don't pass for net win of 0.4 units.
- Point of 6 or 8 and point wins: Player wins 7/6 units on place bet and loses one unit on don't pass for net win of 1/6 units.
- Point of 4 or 10 and point loses: Player loses 1 unit on buy bet and wins one unit on don't pass for net push.
- Point of 5 or 9 and point loses: Player loses 1 unit on place bet and wins one unit on don't pass for net push.
- Point of 6 or 8 and point loses: Player loses 1 unit on place bet and wins one unit on don't pass for net push.
The following table summarizes all the possible outcomes. The table shows the probability, win, and contribution to the return for all possible outcomes. The lower right cell shows an expected loss of 0.02951 units.
Right and Wrong Way System
| Event | Pays | Probability | Return |
|---|---|---|---|
| Come out 2 or 3 | 1 | 0.083333 | 0.083333 |
| Come out 12 | 0 | 0.027778 | 0.000000 |
| Come out 7 or 11 | -1 | 0.222222 | -0.222222 |
| Point 4 win | 0.95 | 0.027778 | 0.026389 |
| Point 5 win | 0.4 | 0.044444 | 0.017778 |
| Point 6 win | 0.166667 | 0.063131 | 0.010522 |
| Point 8 win | 0.166667 | 0.063131 | 0.010522 |
| Point 9 win | 0.4 | 0.044444 | 0.017778 |
| Point 10 win | 0.95 | 0.027778 | 0.026389 |
| Point 4 loss | 0 | 0.055556 | 0.000000 |
| Point 5 loss | 0 | 0.066667 | 0.000000 |
| Point 6 loss | 0 | 0.075758 | 0.000000 |
| Point 8 loss | 0 | 0.075758 | 0.000000 |
| Point 9 loss | 0 | 0.066667 | 0.000000 |
| Point 10 loss | 0 | 0.055556 | 0.000000 |
| Total | 1.000000 | -0.029512 |
The reason this strategy has a negative expected value is on the come out roll. There are 3 ways to win on the 2 or 3 and 8 ways to lose on the 7 or 11. It is true that if the player survives the come out roll he has positive equity, but it isn't enough to overcome the expected loss on the come out roll.
My wife is angry 20% of the time. When asked "Are you angry?" she will say "no" 90% of the time when angry. When asked the same question when she is not angry, she will say "no" 95% of the time. My question what is the probability she is angry according to the answer to the question?
This is a classic Bayesian probability question.
If she answers "no", the probability she is mad is 9/47 = 19.15%.
If she answers "yes", the probability she is mad is 1/3 = 33.33%.
The formula for the answer to questions expressed as "if A then B" is probability(both A and B)/probability(B).
In the case of a "no" answer, the probability she is mad is (0.2*0.9)/(0.2*0.9 + 0.8*0.95) = 0.18/0.94 = 9/47.
In the case of a "yes" answer, the probability she is mad is (0.2*0.1)/(0.2*0.1 + 0.8*0.05) = 0.02/0.06 = 1/3.




