Ask The Wizard #386
I'm aware that if you win $1,200 or more on a machine you have the option to be paid by check. That said, let's say, for the sake of argument, that I wish to convert cash to checks issued by a casino. Please assume I play 9/6 Jacks or Better perfectly at a $25 denomination (or $125 total bet). How much of my cash could I expect to lose converting it to checks?
For 9-6 Jacks or Better you will win $1200 or more with every four of a kind or higher. The return for a full house and less is 0.911103. You'll have to churn though your original bankroll 1/(1-0.911103) = 11.249016 times until your cash has either been converted to check or lost to the house edge. The house edge is 0.004561. Thus, you can expect to lose 0.004561 × 11.249016 = 0.051306 times your original bankroll.
Interestingly, the cost to convert cash to checks is less in 9-6 Double Double Bonus, despite the higher house edge. That game has higher wins for all four of a kinds, so your checks are larger. In that game, the return from a full house and less is 0.777138. That means, you'll have to cycle through your bankroll 1/(1-0.777138) = 4.487076 times to convert it to check. The house edge in 9-6 double double bonus is 0.010192. Thus, the expected loss converting to cash is 4.487076 × 0.010192 = 0.045733.
You could cut down the cost even more with strategy deviations that target four of a kinds and higher, but I'll leave that as an exercise for the reader.
This question is asked and discussed in my forum at Wizard of Vegas.
What's your opinion of the Marching Soldier strategy in craps?
For the benefit of other readers, let me explain what the Marching Soldier is. Briefly, it's a method of parlaying $5 into $1,200. You do have to add more money to it sometimes, so that wins are evenly divisible by $1. Here are the specifics of how it works on a table where you must pre-pay the commission on the 4 and 10:
- Make $5 place bet on the 4.
- If step 1 wins, then take $14 win* plus $1 from your stack and make $15 place bet on the 5.
- If step 2 wins, then make $36 place bet on the 6.
- If step 3 wins, then make $78 place bet on the 8.
- If step 4 wins, then bet $169 win plus $1 from your stack on the 9.
- If step 5 wins, then you will have $408. Take $12 from your stack to pay the $20 commission on a $400 buy bet on the 10.
- If step 6 wins, then take down the $1200.
- If any bet loses, then you're done.
*: By "win" I include the original bet amount.
You may also do this in the reverse order, starting with 10 and ending with 4.
If you make it all the way to the end, you'll have a net win of $1,181, after deducting the $5 in initial and $14 in subsequent wagers from your stack.
The probability of success is 0.3673%, or 1 in 272.
If you play at a table where the commission on the 4 and 10 is paid after a win only, then instead of adding $12 from your pocket after a win on the 9, I would put $8 into it. Then you'll have an even $400 on the 10, for which you'll get back $1,180 if you win. This more generous rule results in an expected net win of $1,188.
If we define the house edge as the expected loss to the expected wager, it is 19.76% if the commission must be paid in advance and 17.03% if it is paid after a win only.
This question is asked and discussed in my forum at Wizard of Vegas.
Newspapers in 1944 noticed this incredible coincidence:
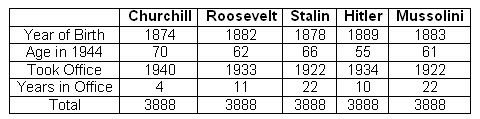
Is this a big coincidence or is there some mathematical gimmick involved?
It's a mathematical gimmick and the basis of a known magic trick.
For everyone alive in 1944, the sum of their age (after their birthday) and their year of birth was 1944. Think about it. If you were x years old then you were born in 1944-x. The sum is x + (1944-x) = 1944.
It's the same thing the "years in office" in 1944. If you were in office y years, then you must have started in 1944-y. y + (1944-y) = 1944.
The sum of 1944 + 1944 = 3,888. Works every time.
To turn this into a magic trick that works in 2023, as a subject to take the sum of the following four things:
- Year of their birth
- How old will they turn this year.
- Year some significant event happened (like birth of first child).
- Anniversary of that significant event this year.
It will always sum to 2023 + 2023 = 4046.
This question is asked and discussed in my forum at Wizard of Vegas.




