Ask The Wizard #379
Thank you for your advice to play STARE as the first turn in Wordle. My question is what should I play on the second turn, according to the score I get after playing STARE?
The following table shows my recommended second word, according to how you do after playing STARE. I list every situation where the sum of yellows and greens is 0 to 2. In two situation, I found there was no valid word.
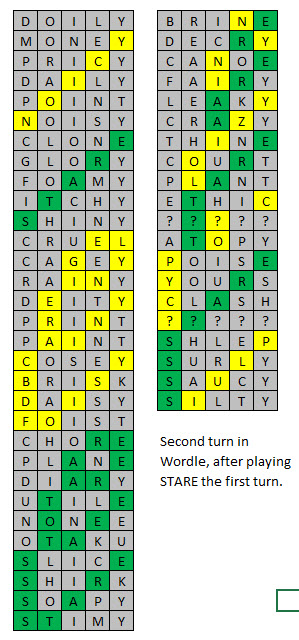
For example, if STARE results in only a yellow in the fifth position (from the left), then play MONEY as your second turn.
My advice is based mostly on which word has the most frequently used letters, especially in those positions. However, I also gave some consideration to words I head of. For a list of my top ten for situation, please see my post on this topic at Wizard of Vegas.
What is your opinion of the Doey Don't strategy in craps?
For those not familiar with it, the Doey Don't works as follows:
- On a come-out roll, make both a pass and don't pass bet, for the same amount.
- If a point is rolled, bet the odds on it.
The thinking is the don't pass bet is a hedge against a 7-out on the come-out roll. Players who play the doey don't would probably say the pass and don't offset each other, letting the player enjoy the odds bet with no house advantage.
The flaw is if a 12 is rolled on the come-out roll. The pass will lose and the don't pass will push, resulting in a loss of one unit. The probability of a 12 is 1/36, making the expected loss with this strategy 1/36 = 2.78% of one unit. Meanwhile, the expected loss making just a pass bet and taking the odds 7/495 = 1.41% of one unit.
However, the Doey Don't has less volatility. Assuming 3-4-5x odds, here is the standard deviation both ways:
- Pass + full odds: 4.915632
- Doey Don't: 4.085789
The bottom line is I don't recommend the Doey Don't, because the expected loss is 1.36% of a unit more.
A pair of two fair six-sided dice are rolled over and over until one of the following two events occur:
A) A total of 12 is rolled.
B) A total of 7 is rolled two times consecutively.
Which is more likely to happen first?
> [spoiler=Solution]
Let:
- p = Probability the 12 is rolled first from the initial state or anytime the previous roll was not a 7.
- q = Probability the 12 is rolled first when the previous roll was a 7.
This is what is known as a Markov Chain problem.
Before we get to that, recall the probability of rolling a total of 7 is 1/6 and that of a 12 is 1/36.
We can define p and q in terms of each other, as follows:
- (1) p = (1/36) + (6/36)q + (29/36)p
- (2) q = (1/36) + (29/36)p
Let's multiply equation (1) by 36:
36p = 1 + 6q + 29p
(3) 7p = 1 + 6q
Let's substitute the value for q in (2) into (3):
7p = 1 + 6*((1/36) + (29/36)p)
7p = 1 + (1/6) + (29/6)p
42p = 6 + 1 + 29p
13p = 7
q = 7/13
So, the probability of rolling the 12 first is 7/13 =~ 53.85%.
The probability of rolling two consecutive 7's first is thus 46.15%.
Thus, it's more likely the total of 12 is rolled first.




