Ask The Wizard #352
How much do maximum payouts increase the house edge in Mississippi Stud?
Good question. Mississippi Stud players definitely should be aware that maximum payouts may reduce what they win on a royal flush, which serves to increase the house edge.
The top pay in Mississippi Stud is 500 to 1 for a royal flush and it applies to all bets. The player has two chances to raise up to 3x his Ante, so his final bet can be up to 7x his Ante. If the player has hope for a Royal, he should be maxing the maximum raises.
The most the player should bet on the Ante in Mississippi Stud, without being affected by a payout cap, is the maximum payout/3500. For example, if the maximum payout is $80,000, then the most I advise betting on the Ante is $22.86. I would round that down to $20.
The following table shows the house edge at various bets and common maximum wins. The table assumes optimal player strategy with no cap on wins. Note how the house edge increases as bet size increases and the cap decreases.
House Edge with Payout Cap
| Bet | $50,000 Cap | $80,000 Cap | $100,000 Cap |
|---|---|---|---|
| $15 | 5.02% | 4.91% | 4.91% |
| $20 | 5.15% | 4.91% | 4.91% |
| $25 | 5.22% | 5.04% | 4.91% |
| $50 | 5.38% | 5.28% | 5.22% |
| $75 | 5.49% | 5.37% | 5.33% |
| $100 | 5.64% | 5.41% | 5.38% |
This question is asked and discussed in my forum at Wizard of Vegas.
Vital Vegas has taken a player to task for tipping only $200 on a $1.1 million jackpot. What is the appropriate etiquette for tipping in such a situation?
Yes, while they chastise the player for the small tip, they conveniently dodge the question on what an appropriate tip should be.
Not only is tipping etiquette not well defined for big jackpots, it isn't even well defined for small ones. Opinions range all over the place, many of them by people who have never won a jackpot.
First, let me emphasize that tipping is not optional. It is expected to tip in a casino for the service you receive, according to the amount won and level of service. It is easy to become Mr. Pink at this point and rationalize why they shouldn't tip for anything. Tipping is definitely a flawed system, but it is the system we have. If you don't agree and refuse to tip, then don't ask for whatever service it is expected to tip for.
Second, once it's established the player should tip for jackpot, how much? I am limiting this discussion for the kind of situation where the player hits just one jackpot. Rules are different if the player hits lots of them, which is normal at very high bet levels. Remember, the rules to go through the jackpot paperwork are:
- Win of $1,200 or more on "slots".
- Win of $1,500 or more in keno.
- Win of $5,000 or more in a a poker tournament.
- Win of $600 or more AND at least 300x the wager in table games.
What do I recommend tipping? In the past I have said 0.5% to 2% of the jackpot, the greater the jackpot, the lower the percentage. However, I wasn't thinking of jackpots this big at the time. That range I think is appropriate up to about $100,000.
This question has caused me to create a specific formula, which I think is appropriate for any jackpot from $1200 to into the millions. Here it is:
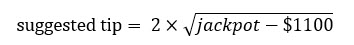
If you can't see the image, it is 2×sqrt(jackpot-$1100).
Here is what the formula gives for some common jackpot amounts.
Suggested Tip Table
| Jackpot | Tip |
|---|---|
| $1,200 | $20 |
| $2,000 | $60 |
| $5,000 | $125 |
| $10,000 | $189 |
| $20,000 | $275 |
| $50,000 | $442 |
| $100,000 | $629 |
| $1,000,000 | $1,999 |
In the case of $1.1 million, my formula suggests $2,096.57. I think it is fine to round down to $2,000. Of course, also consider other factors such as the quality of the service.
This question is raised and discussed in my forum at Wizard of Vegas.
For any given large number, what is the average distance between primes near that number? Also, how many primes are there less than that number?
A very good estimate for the average distance between primes near any large number n is ln(n). It is remarkable how how good this estimator is.
As evidence, the following table shows the range of the first 15 million primes, in groups of one million. The table shows the average distance in the range between primes and the estimate of the average distance. The estimate is the natural log of the average of the largest and smallest prime in the range. For example, for the 15th group of a million primes, it is ln((256,203,221+275,604,541)/2).
Average Distance Between Primes
| First Prime in Range |
Last Prime in Range |
Primes in Range |
Average Distance | Estimate | |
|---|---|---|---|---|---|
| 2 | 15,485,863 | 1,000,000 | 15.485861 | 15.86229105 | |
| 15,485,867 | 32,452,843 | 1,000,000 | 16.966976 | 16.9922867 | |
| 32,452,867 | 49,979,687 | 1,000,000 | 17.52682 | 17.53434381 | |
| 49,979,693 | 67,867,967 | 1,000,000 | 17.888274 | 17.89175615 | |
| 67,867,979 | 86,028,121 | 1,000,000 | 18.160142 | 18.15864108 | |
| 86,028,157 | 104,395,301 | 1,000,000 | 18.367144 | 18.3716137 | |
| 104,395,303 | 122,949,823 | 1,000,000 | 18.55452 | 18.54883262 | |
| 122,949,829 | 141,650,939 | 1,000,000 | 18.70111 | 18.70058553 | |
| 141,650,963 | 160,481,183 | 1,000,000 | 18.83022 | 18.83322787 | |
| 160,481,219 | 179,424,673 | 1,000,000 | 18.943454 | 18.95103217 | |
| 179,424,691 | 198,491,317 | 1,000,000 | 19.066626 | 19.05703535 | |
| 198,491,329 | 217,645,177 | 1,000,000 | 19.153848 | 19.15337672 | |
| 217,645,199 | 236,887,691 | 1,000,000 | 19.242492 | 19.24163365 | |
| 236,887,699 | 256,203,161 | 1,000,000 | 19.315462 | 19.32305683 | |
| 256,203,221 | 275,604,541 | 1,000,000 | 19.40132 | 19.39864545 |
Source: The Gaps Between Primes at Prime Pages.
To get the number of primes under any given number, we can start by integrating the average distance estimate of ln(n). This will give us the sum of average distances between primes up to any number n.
What is the integral of f(n)=ln(n)? Recall that integration by parts tells us:
Integral of f(n)*g'(n) dn = f(n)*g(n) - integral of (f'(n)*g(n)) dn
Let f(n)=ln(n) and g'(n)=1. Then f'(n)=1/n and g(n)=n. The integral of ln(n) will thus be ln(n)*n - integral of ((1/n)*n) = ln(n)*n - n = n*(ln(n)-1)
If we divide n*(ln(n)-1) by n, we get the average distance between primes for the range of numbers from 2 to n. This is ln(n)-1.
If we divide n by this average distance between primes, we get the average number of primes under n, which equals n/(ln(n)-1).
As evidence, the following table shows the number of primes under various large numbers and the estimated value. Please excuse the 15 significant digits of precision, which is all Excel will allow. Somebody, please, make a spreadsheet that can handle more.
Average Distance Between Primes
| n | Primes under n | n/(ln(n)-1) |
|---|---|---|
| 10 | 4 | 8 |
| 100 | 25 | 28 |
| 1,000 | 168 | 169 |
| 10,000 | 1,229 | 1,218 |
| 100,000 | 9,592 | 9,512 |
| 1,000,000 | 78,498 | 78,030 |
| 10,000,000 | 664,579 | 661,459 |
| 100,000,000 | 5,761,455 | 5,740,304 |
| 1,000,000,000 | 50,847,534 | 50,701,542 |
| 10,000,000,000 | 455,052,511 | 454,011,971 |
| 100,000,000,000 | 4,118,054,813 | 4,110,416,301 |
| 1,000,000,000,000 | 37,607,912,018 | 37,550,193,650 |
| 10,000,000,000,000 | 346,065,536,839 | 345,618,860,221 |
| 100,000,000,000,000 | 3,204,941,750,802 | 3,201,414,635,781 |
| 1,000,000,000,000,000 | 29,844,570,422,669 | 29,816,233,849,001 |
| 10,000,000,000,000,000 | 279,238,341,033,925 | 279,007,258,230,820 |
| 100,000,000,000,000,000 | 2,623,557,157,654,230 | 2,621,647,966,812,030 |
| 1,000,000,000,000,000,000 | 24,739,954,287,740,800 | 24,723,998,785,920,000 |
| 10,000,000,000,000,000,000 | 234,057,667,276,344,000 | 233,922,961,602,470,000 |
| 100,000,000,000,000,000,000 | 2,220,819,602,560,910,000 | 2,219,671,974,013,730,000 |
| 1,000,000,000,000,000,000,000 | 21,127,269,486,018,700,000 | 21,117,412,262,910,000,000 |
| 10,000,000,000,000,000,000,000 | 201,467,286,689,315,000,000 | 201,381,995,844,660,000,000 |
| 100,000,000,000,000,000,000,000 | 1,925,320,391,606,800,000,000 | 1,924,577,459,166,810,000,000 |
| 1,000,000,000,000,000,000,000,000 | 18,435,599,767,349,200,000,000 | 18,429,088,896,563,900,000,000 |
| 10,000,000,000,000,000,000,000,000 | 176,846,309,399,143,000,000,000 | 176,788,931,049,964,000,000,000 |
Source: How Many Primes are There? at Prime Pages.


