Ask The Wizard #338
What is the average number of rolls needed with two dice to achieve every total from 2 to 12?
One could use a Markov chain to answer this, but I prefer calculus. The key is that the answer is the same if the time between rolls is the exponentially distributed with a mean of one. That said, the answer can be expressed as the integral from 0 to infinity of:
1-(1-exp(-x/36))^2*(1-exp(-x/18))^2*(1-exp(-x/12))^2*(1-exp(-x/9))^2*(1-exp(-5*x/36))^2*(1-exp(-x/6))
You may easily solve such integrals with an integral calculator.
You may also solve any such problem with my Expected Trials Calculator.
There is an ant in the middle of a square. He is 17" from the upper-left corner, 20" from the upper-right corner, and 13" from the lower-right corner.
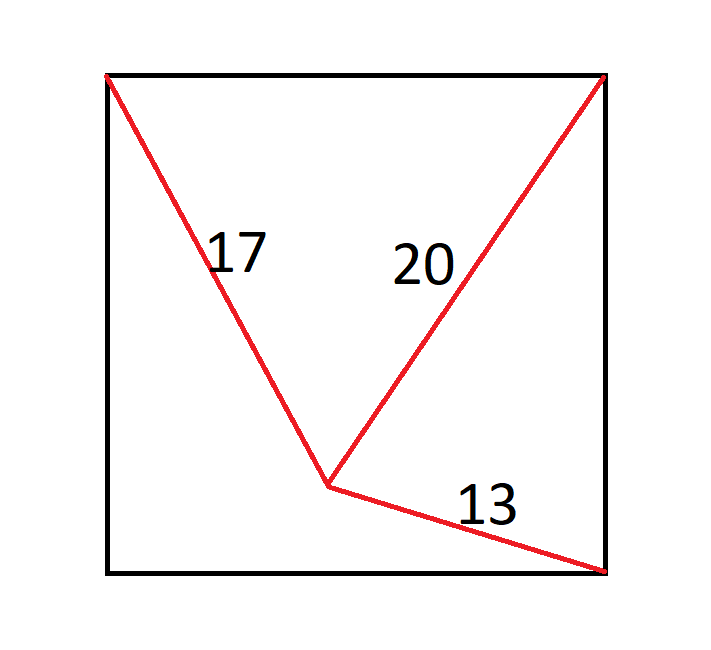
How large is the square?
cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b)
First, rotate triangle ABE 90 degrees to form a new triangle BDF.
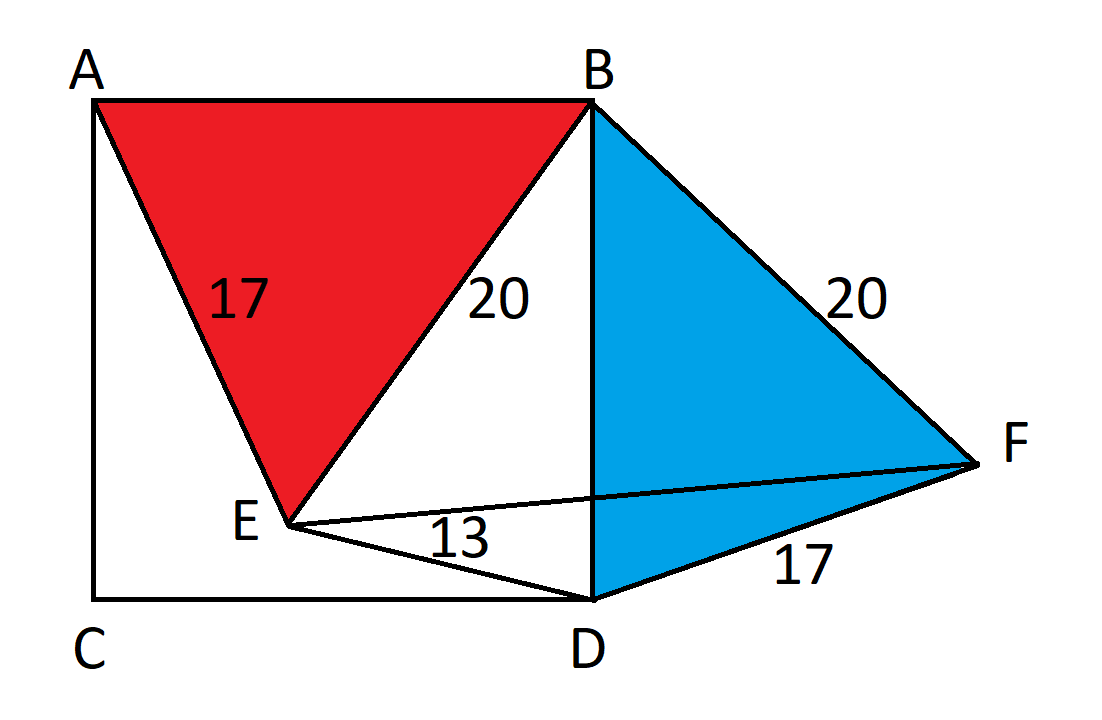
Since the triangle was rotated 90 degrees, angle EBF=90, by definition. By the Pythagorean formula, EF = 20*sqrt(2).
By the law of cosines: 17^2 = 13^2 + (20*sqrt(2))^2 - 2*13*20*sqrt(2)*cos(DEF).
289 = 169 + 800 - 520*sqrt(2)*cos(DEF)
520*sqrt(2)*cos(DEF) = 680.
cos(DEF) = 17*sqrt(2)/26.
Recall, sin^2(x) + cos^2(x) = 1. Let's use that to solve for sin(DEF).
sin^2(DEF) + cos^2(DEF) = 1
sin^2(DEF) + (17*sqrt(2)/26)^2 = 1
sin^2(DEF) + 289/338 = 1
sin^2(DEF) = 49/338
sin(DEF) = 7*sqrt(2)/26
Next, consider angle BED.
Angle BED = Angle BEF + Angle FED.
We know EBF is 90 degrees and an isosceles triangle. That would make angle BEF 45 degrees.
So, Angle BED = 45 degrees + Angle FED.
Recall, cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b).
cos(BED) = cos(BEF + FED) = cos(BEF)*cos(FED) - sin(BEF)*sin(FED)
= (1/sqrt(2))*17*sqrt(2)/26 - (1/sqrt(2))*7*sqrt(2)/26
= (17/26) - (7/26) = 10/26 = 5/13
Let's apply the law of cosines again, this time to triangle BED.
BD^2 = 20^2 + 13^2 - 2*20*13*(5/13)
= 400 + 169 - 200 = 369
BD is the side of the square in question, so BD^2 is the area of that square, which we have shown is 369.
This question is asked and discussed in my forum at Wizard of Vegas.
Drop Dead is a game played with five standard dice. You begin your turn by rolling all five dice. If none of them are a 2 or 5, you total the dice, add the sum to your point score and roll again. If you do roll any 2s or 5s, your score for the roll is zero. All the dice showing a 2 or 5 are declared dead and set aside. You then roll again with the remaining dice. Play continues with you either scoring points or removing dice. Your turn ends when all your dice are eliminated whereupon you are said to have dropped dead. All your scoring rolls are added together for your final score. High score wins.
What is your expected score for this game?
Let's start with the scenario with one die left and move backwards.
Let the variable a be the expected additional points with one die left.
The average roll that isn't a 2 or 5 is (1+3+4+6)/4 = 7/2.
a = (2/3)×(a + 7/2).
a/3 = 7/3.
a = 7.
Next, let's calculate b, the expected points with two dice left.
b = (2/3)2×(b + 2 × (7/2)) + 2×(2/3)×(1/3)×a.
b = 11.2.
Next, let's calculate c, the expected points with three dice left.
c = (2/3)3×(c + 3× (7/2)) + 3×(2/3)2×(1/3)×b + 3×(2/3)×(1/3)2×b.
c = 1302/95 = 13.705263.
Next, let's calculate d, the expected points with four dice left.
d = (2/3)4×(d + 4× (7/2)) + 4×(2/3)3×(1/3)×c + 6×(2/3)2×(1/3)2×b + 4×(2/3)×(1/3)3×a.
d = 3752/247 = 15.190283.
Finally, let's calculate e, the expected points with five dice left.
e = (2/3)5×(e + 5×(7/2)) + 5×(2/3)4×(1/3)×d + 10×(2/3)3×(1/3)2×c + 10×(2/3)2×(1/3)3×b + 5×(2/3)×(1/3)4×a.
e = 16.064662.
This question is asked and discussed in my forum at Wizard of Vegas.
Consider the Pairplus bet in Three Card Poker, that follows the 1-4-6-30-40 pay table. However, it pays a jackpot for a mini-royal in spades and 25% of that jackpot for a mini royal in the other three suits. How high the meter need to be for the bet to be fair?
The answer is 384 times the bet amount.
For every additional 100 bets above that, the return goes up by 0.79%.
This question is asked and discussed in my forum at Wizard of Vegas.




