Ask The Wizard #321
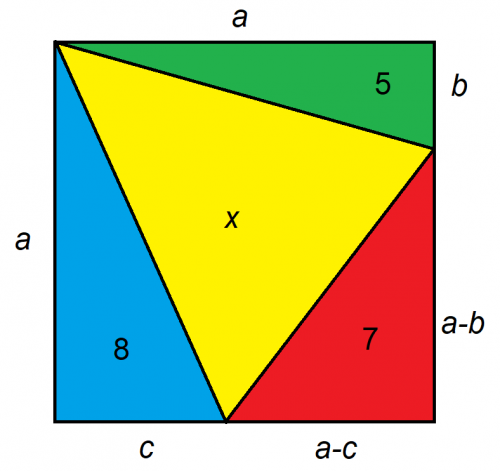
Given the larger figure is a square, what is the area of x?
The key to problems like this is in setting them up. I recommend trying to boil the problem down to as few unknowns as possible. In this case, we can express the unknown distances on the square to just three, as follows:
It's easier to deal with rectangles than triangles. Given we know the area of three triangles, we can double the size and double the areas. That gives us:
- ab=10
- ac=16
- (a-b)(a-c)=14
Let's factor (a-b)(a-c):
a2 - ab- ac + bc = 14
a2 - 10 - 16 + bc = 14
(1) a2 + bc = 40
Let's express b and c in terms of a, to get this down to a single variable:
b = 10/a
c = 16/a
Substituting those values for b and c in equation (1):
a2 + (10/a)*(16/a) = 40
a2 + 160/a2 = 18
Next, let's get rid of that a2 in the denominator by multiplying everything by a2.
a4 + 160 = 40*a2
a4 - 40*a2 + 160 = 0
Let's define a new variable y = a2
y2 - 18y + 32 = 0
Next, let's solve for y using the quadratic formula:
y = (40 +/- sqrt(1600-640))/2
y = (40 +/- sqrt(960))/2
y = (40 +/- 8*sqrt(15))/2
y = 20 +/- 4*sqrt(15)
The area of the entire square is a2, which conveniently is equal to y. From the equation above, if the +/- is negative, then y = apx 4.5081, which is obviously wrong, since we know the area is at least 20, not even including x. So that area of the square must be 20 + 4*sqrt(15).
The three triangles we're given have an area of 5+7+8=20. Subtracting that from the total area of the square leaves us the area of x: 20 + 4*sqrt(15) - 20 = 4*sqrt(15) = apx 15.4919.
This question is raised and discussed in my forum at Wizard of Vegas.

Note my t-shirt in this picture. The movie theater cashier complimented it when I went to see Uncut Gems. I thanked her by torturing her with this problem, only with triangles of areas 2, 3 and 4. After the movie, I checked on her and she still hadn't solved it, but seemed to be trying. So I wrote out the following solution at the Suncoast bar for her. She actually seemed to appreciate it. I think that young woman will go far in life.
Regarding the Lottery, os there a jackpot size "tipping point" in multi-state lotteries (Powerball, Mega Millions) where it is more likely that the big prize will be split than there will be a single winner? If so, what is that amount?
I won't go into all the math, but here are the jackpot points where multiple winners are equally likely as exactly one:
- PowerBall: $975 million
- Mega Millions: $1.65 billion
Not that you asked, but here are the jackpots where the probability of at least one winner is equal to the probability of none (50%).
- PowerBall: $704 million
- Mega Millions: $867 million
This question is raised in discussed in my forum at Wizard of Vegas.
- In a jail there are 12 prisoners, each numbered 1 to 12.
- The warden sets up 12 boxes, each numbered 1 to 12.
- Inside the 12 boxes are the numbers 1 to 12, randomly placed, one in each box.
- Each prisoner, one at a time, shall be allowed to open six boxes of his choosing. He may choose and open them one at a time.
- Each prisoner's goal is to find his own number inside a box, among his six choices. If he does, that person is said to survive.
- If a prisoner does not find his own number, then the entire group is said to fail and they will be immediately be walked over to a firing squad.
- If a prisoner survives, then he must place the numbers back in their original boxes for the next prisoner.
- Prisoners may not watch other players or communicate once the game begins.
- Before beginning, the entire group is allowed to collaborate on a strategy. The goal is for all 12 prisoners to survive (in other words find his own number inside a box).
What should their strategy be to maximize their probability of survival and what is that probability?
Much like a Secret Santa game, there will be loops leading from one number to another. With 12 prisoners, there can be 1 to 12 loops. If no loop is longer than six, then every prisoner will eventually find his number. The big question is what is the probability of no loop larger than six? Let's reverse it and find the number of combinations of a loop size of 7 or more.
12 Prisoner Solution
| Loops | Combinations | Probability |
|---|---|---|
| 12 | 39,916,800 | 0.083333 |
| 11,1 | 43,545,600 | 0.090909 |
| 10,2 | 23,950,080 | 0.050000 |
| 10,1,1 | 23,950,080 | 0.050000 |
| 9,3 | 17,740,800 | 0.037037 |
| 9,2,1 | 26,611,200 | 0.055556 |
| 9,1,1,1 | 8,870,400 | 0.018519 |
| 8,4 | 14,968,800 | 0.031250 |
| 8,3,1 | 19,958,400 | 0.041667 |
| 8,2,2 | 7,484,400 | 0.015625 |
| 8,2,1,1 | 14,968,800 | 0.031250 |
| 8,1,1,1,1 | 2,494,800 | 0.005208 |
| 7,5 | 13,685,760 | 0.028571 |
| 7,4,1 | 17,107,200 | 0.035714 |
| 7,3,2 | 11,404,800 | 0.023810 |
| 7,3,1,1 | 11,404,800 | 0.023810 |
| 7,2,2,1 | 8,553,600 | 0.017857 |
| 7,2,1,1,1 | 5,702,400 | 0.011905 |
| 7,1,1,1,1,1 | 570,240 | 0.001190 |
| Total | 312,888,960 | 0.653211 |
The following table shows the formulas for the combinations in the table above.
Combination Formulas
| Loops | Combinations | Formula |
|---|---|---|
| 12 | 39916800 | =FACT(11) |
| 11,1 | 43545600 | =COMBIN(12,11)*FACT(10) |
| 10,2 | 23950080 | =COMBIN(12,10)*FACT(9) |
| 10,1,1 | 23950080 | =COMBIN(12,10)*FACT(9) |
| 9,3 | 17740800 | =COMBIN(12,9)*FACT(8)*FACT(2) |
| 9,2,1 | 26611200 | =COMBIN(12,9)*COMBIN(3,2)*FACT(8) |
| 9,1,1,1 | 8870400 | =COMBIN(12,9)*FACT(8) |
| 8,4 | 14968800 | =COMBIN(12,8)*FACT(7)*FACT(3) |
| 8,3,1 | 19958400 | =COMBIN(12,8)*COMBIN(4,3)*FACT(7)*FACT(2) |
| 8,2,2 | 7484400 | =COMBIN(12,8)*COMBIN(4,2)*FACT(7)/2 |
| 8,2,1,1 | 14968800 | =COMBIN(12,8)*COMBIN(4,2)*FACT(7) |
| 8,1,1,1,1 | 2494800 | =COMBIN(12,8)*FACT(7) |
| 7,5 | 13685760 | =COMBIN(12,7)*FACT(6)*FACT(4) |
| 7,4,1 | 17107200 | =COMBIN(12,7)*5*FACT(6)*FACT(3) |
| 7,3,2 | 11404800 | =COMBIN(12,7)*COMBIN(5,3)*FACT(6)*FACT(2) |
| 7,3,1,1 | 11404800 | =COMBIN(12,7)*COMBIN(5,3)*FACT(6)*FACT(2) |
| 7,2,2,1 | 8553600 | =COMBIN(12,7)*COMBIN(5,2)*COMBIN(3,2)*FACT(6)/2 |
| 7,2,1,1,1 | 5702400 | =COMBIN(12,7)*COMBIN(5,2)*FACT(6) |
| 7,1,1,1,1,1 | 570240 | =COMBIN(12,7)*FACT(6) |
From the lower right cell of the first table, there are 312,888,960 losing combinations. The total number of ways the numbers can be arranged is 12! = 479,001,600. Thus, the probability of failure is 312,888,960 / 479,001,600 = 65.32%. Therefore, the probability of success is 100% - 65.32% = 34.68%.
This question is raised and discussed in my forum at Wizard of Vegas.
Hello. I have a coupon that allows me to push a hand of 22. I can hold onto the coupon until my first 22. It doesn't apply to doubles or splits. What is the value of this?
A quick answer is the value of the maximum you're allowed to bet. Just wait for a 22 and then play it, resulting in walking away from the table with an extra unit.
A more rigorous answer should look at the cost of waiting for that 22. This is something I don't know exactly, but can estimate.
The cost to the player of the dealer-push-22 rule is 6.91%. However, the dealer will get to 22 more than that, because the player won't care if he busted first. Depending on the rules, the player will bust about 15.7% of the time. If we assume this is uncorrelated with the dealer's probability of busting (which it's not), then the probability of a dealer bust is 6.91%/(1.0-0.157) = 8.2%.
I know this is rough, but let's assume the player's 22 probability is the same. I know the dealer will bust more than the player, but this coupon also doesn't count after a split, so let's just say those factors offset. So, if the player gets a 22 8.2% of hands, then he will get a 22 once every 1/0.082 = 12.2 hands on average.
Let's say the house edge in the base game is 0.75%. The cost of playing 12.2 hands at that house edge is 12.2*0.0075 = 0.0915. So, subtract that from the one unit value and you get a value of the coupon of 1.0 - 0.0915 about 91% of face value.
This question is raised and discussed in my forum at Wizard of Vegas.