Ask The Wizard #307
I'm participating in a 2018 "dead pool." Here are the rules:
- Each player must submit a list of ten living celebrities under age 100.
- If any celebrity dies, as evidenced by a mention by the Associated Press, in 2018, then anyone with the celebrity's name on his list will receive 100-x points, where x is the age at death.
- Player with the most points on 1/1/2019 wins.
Going off of averages, what is the optimal strategy for this game?
As a former actuary, you asked the right person. Hopefully the Society of Actuaries will not consider my answer an abuse of the profession. That said, to answer your question I consulted a 2014 Period Life Table from my former place of work, the Office of the Chief Actuary of the Social Security Administration.
A period life table shows, among other things, the probability of death for a person of any given age and gender in 2014. Using that information I created the following table, which shows both the probability of death and expected points for all ages from 0 to 100 and both genders.
2014 Period Life Table Death Pool
| Age | Probability of Death — Male |
Probability of Death — Female |
Expected Points — Male |
Expected Points — Female |
|---|---|---|---|---|
| 0 | 0.006320 | 0.005310 | 0.632000 | 0.531000 |
| 1 | 0.000403 | 0.000352 | 0.039852 | 0.034835 |
| 2 | 0.000282 | 0.000221 | 0.027626 | 0.021683 |
| 3 | 0.000211 | 0.000161 | 0.020514 | 0.015612 |
| 4 | 0.000181 | 0.000131 | 0.017405 | 0.012556 |
| 5 | 0.000161 | 0.000111 | 0.015313 | 0.010515 |
| 6 | 0.000141 | 0.000111 | 0.013260 | 0.010405 |
| 7 | 0.000131 | 0.000101 | 0.012184 | 0.009360 |
| 8 | 0.000121 | 0.000091 | 0.011127 | 0.008334 |
| 9 | 0.000091 | 0.000081 | 0.008256 | 0.007328 |
| 10 | 0.000101 | 0.000091 | 0.009073 | 0.008154 |
| 11 | 0.000101 | 0.000081 | 0.008973 | 0.007168 |
| 12 | 0.000131 | 0.000101 | 0.011535 | 0.008861 |
| 13 | 0.000202 | 0.000131 | 0.017547 | 0.011389 |
| 14 | 0.000303 | 0.000151 | 0.026023 | 0.012992 |
| 15 | 0.000404 | 0.000191 | 0.034304 | 0.016267 |
| 16 | 0.000505 | 0.000232 | 0.042393 | 0.019464 |
| 17 | 0.000616 | 0.000272 | 0.051129 | 0.022582 |
| 18 | 0.000748 | 0.000302 | 0.061316 | 0.024796 |
| 19 | 0.000880 | 0.000343 | 0.071262 | 0.027768 |
| 20 | 0.001022 | 0.000373 | 0.081780 | 0.029855 |
| 21 | 0.001145 | 0.000404 | 0.090445 | 0.031884 |
| 22 | 0.001258 | 0.000444 | 0.098105 | 0.034643 |
| 23 | 0.001310 | 0.000475 | 0.100880 | 0.036546 |
| 24 | 0.001332 | 0.000495 | 0.101246 | 0.037625 |
| 25 | 0.001344 | 0.000526 | 0.100811 | 0.039422 |
| 26 | 0.001377 | 0.000556 | 0.101864 | 0.041162 |
| 27 | 0.001389 | 0.000577 | 0.101371 | 0.042106 |
| 28 | 0.001421 | 0.000608 | 0.102330 | 0.043740 |
| 29 | 0.001454 | 0.000648 | 0.103234 | 0.046036 |
| 30 | 0.001507 | 0.000669 | 0.105517 | 0.046837 |
| 31 | 0.001530 | 0.000710 | 0.105584 | 0.048998 |
| 32 | 0.001574 | 0.000751 | 0.107011 | 0.051084 |
| 33 | 0.001617 | 0.000813 | 0.108364 | 0.054454 |
| 34 | 0.001661 | 0.000864 | 0.109644 | 0.057041 |
| 35 | 0.001716 | 0.000926 | 0.111521 | 0.060194 |
| 36 | 0.001781 | 0.001008 | 0.113970 | 0.064538 |
| 37 | 0.001857 | 0.001081 | 0.116963 | 0.068090 |
| 38 | 0.001933 | 0.001164 | 0.119830 | 0.072145 |
| 39 | 0.002020 | 0.001237 | 0.123207 | 0.075427 |
| 40 | 0.002118 | 0.001340 | 0.127066 | 0.080422 |
| 41 | 0.002258 | 0.001445 | 0.133232 | 0.085232 |
| 42 | 0.002410 | 0.001560 | 0.139778 | 0.090455 |
| 43 | 0.002615 | 0.001696 | 0.149075 | 0.096649 |
| 44 | 0.002843 | 0.001853 | 0.159228 | 0.103761 |
| 45 | 0.003105 | 0.002011 | 0.170771 | 0.110606 |
| 46 | 0.003401 | 0.002191 | 0.183635 | 0.118300 |
| 47 | 0.003742 | 0.002403 | 0.198314 | 0.127342 |
| 48 | 0.004108 | 0.002647 | 0.213613 | 0.137656 |
| 49 | 0.004532 | 0.002894 | 0.231133 | 0.147577 |
| 50 | 0.004994 | 0.003194 | 0.249696 | 0.159718 |
| 51 | 0.005473 | 0.003487 | 0.268191 | 0.170880 |
| 52 | 0.005993 | 0.003794 | 0.287656 | 0.182103 |
| 53 | 0.006565 | 0.004104 | 0.308561 | 0.192871 |
| 54 | 0.007159 | 0.004428 | 0.329324 | 0.203676 |
| 55 | 0.007799 | 0.004767 | 0.350946 | 0.214498 |
| 56 | 0.008475 | 0.005153 | 0.372902 | 0.226729 |
| 57 | 0.009179 | 0.005534 | 0.394696 | 0.237972 |
| 58 | 0.009856 | 0.005889 | 0.413944 | 0.247347 |
| 59 | 0.010575 | 0.006272 | 0.433558 | 0.257150 |
| 60 | 0.011350 | 0.006683 | 0.453991 | 0.267338 |
| 61 | 0.012209 | 0.007180 | 0.476135 | 0.280016 |
| 62 | 0.013061 | 0.007720 | 0.496330 | 0.293355 |
| 63 | 0.013921 | 0.008339 | 0.515084 | 0.308537 |
| 64 | 0.014814 | 0.009029 | 0.533320 | 0.325041 |
| 65 | 0.015831 | 0.009839 | 0.554094 | 0.344371 |
| 66 | 0.016981 | 0.010741 | 0.577354 | 0.365197 |
| 67 | 0.018300 | 0.011752 | 0.603909 | 0.387812 |
| 68 | 0.019778 | 0.012879 | 0.632894 | 0.412117 |
| 69 | 0.021443 | 0.014142 | 0.664734 | 0.438397 |
| 70 | 0.023384 | 0.015613 | 0.701513 | 0.468376 |
| 71 | 0.025547 | 0.017271 | 0.740873 | 0.500852 |
| 72 | 0.027877 | 0.019047 | 0.780560 | 0.533320 |
| 73 | 0.030384 | 0.020918 | 0.820374 | 0.564797 |
| 74 | 0.033098 | 0.022938 | 0.860535 | 0.596385 |
| 75 | 0.036256 | 0.025299 | 0.906400 | 0.632465 |
| 76 | 0.039868 | 0.028043 | 0.956841 | 0.673035 |
| 77 | 0.043883 | 0.031127 | 1.009299 | 0.715914 |
| 78 | 0.048257 | 0.034590 | 1.061657 | 0.760984 |
| 79 | 0.053128 | 0.038456 | 1.115692 | 0.807583 |
| 80 | 0.058709 | 0.043007 | 1.174177 | 0.860145 |
| 81 | 0.065070 | 0.048186 | 1.236322 | 0.915536 |
| 82 | 0.072149 | 0.053762 | 1.298691 | 0.967712 |
| 83 | 0.079906 | 0.059769 | 1.358409 | 1.016065 |
| 84 | 0.088524 | 0.066380 | 1.416378 | 1.062085 |
| 85 | 0.098157 | 0.073823 | 1.472348 | 1.107351 |
| 86 | 0.108904 | 0.082381 | 1.524651 | 1.153334 |
| 87 | 0.120889 | 0.092180 | 1.571556 | 1.198344 |
| 88 | 0.134134 | 0.103305 | 1.609607 | 1.239664 |
| 89 | 0.148707 | 0.115744 | 1.635778 | 1.273180 |
| 90 | 0.164522 | 0.129477 | 1.645220 | 1.294772 |
| 91 | 0.181584 | 0.144435 | 1.634254 | 1.299911 |
| 92 | 0.199903 | 0.160621 | 1.599225 | 1.284970 |
| 93 | 0.219362 | 0.177816 | 1.535534 | 1.244713 |
| 94 | 0.239881 | 0.196194 | 1.439286 | 1.177165 |
| 95 | 0.260293 | 0.214694 | 1.301463 | 1.073469 |
| 96 | 0.280129 | 0.233056 | 1.120515 | 0.932225 |
| 97 | 0.299042 | 0.251152 | 0.897125 | 0.753456 |
| 98 | 0.316317 | 0.268235 | 0.632634 | 0.536471 |
| 99 | 0.332667 | 0.284442 | 0.332667 | 0.284442 |
| 100 | 0.348651 | 0.301417 | 0.000000 | 0.000000 |
The table shows that the maximum expected points is for a 90 year-old-man at 1.645220.
This question is raised and discussed in my non-gambling forum, Diversity Tomorrow.
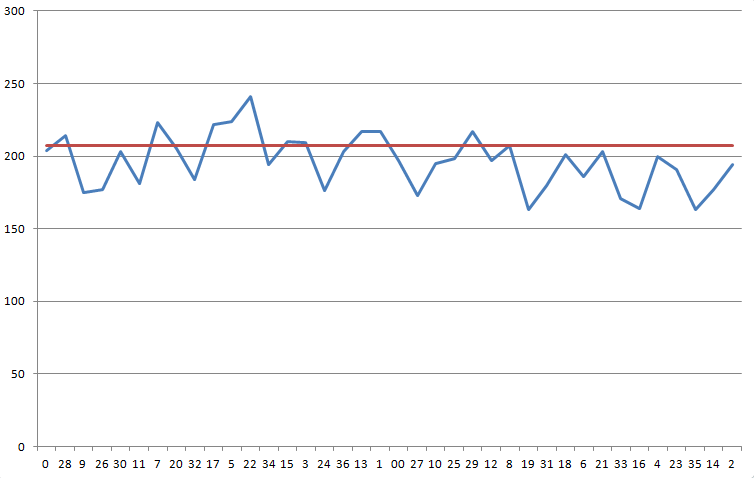
I recorded 7,456 spins in roulette. The results are as follows. I suspect the wheel is biased but am not sure if the data is conclusive enough to play it.
Roulette Data
| Winning Number |
Occurences |
|---|---|
| 0 | 204 |
| 28 | 214 |
| 9 | 175 |
| 26 | 177 |
| 30 | 203 |
| 11 | 181 |
| 7 | 223 |
| 20 | 205 |
| 32 | 184 |
| 17 | 222 |
| 5 | 224 |
| 22 | 241 |
| 34 | 194 |
| 15 | 210 |
| 3 | 209 |
| 24 | 176 |
| 36 | 203 |
| 13 | 217 |
| 1 | 217 |
| 00 | 197 |
| 27 | 173 |
| 10 | 195 |
| 25 | 198 |
| 29 | 217 |
| 12 | 197 |
| 8 | 207 |
| 19 | 163 |
| 31 | 180 |
| 18 | 201 |
| 6 | 186 |
| 21 | 203 |
| 33 | 171 |
| 16 | 164 |
| 4 | 200 |
| 23 | 191 |
| 35 | 163 |
| 14 | 177 |
| 2 | 194 |
| Total | 7456 |
The following graph shows your results in sequential order on the wheel. The blue line shows your results. The red line is the number you need, 207.11, to overcome the 5.26% house edge.
A chi-squared test on this distribution comes back with a statistic of 68.1 with 37 degrees of freedom. The probability of a result this skewed or more is 1 in 725.
I don't think the chi-squared is the perfect test for this situation because it doesn't consider the ordering of the outcomes, but don't know of a better test. Some have suggested the Kolmogorov–Smirnov test, but I don't think that is appropriate. If there are any other appropriate tests, I'm all ears.
I can say if you had bet the 3-number arc around the number 5, you would have had a 10.57% profit over the spins you recorded. However, if you increased that to a 7-number arc, the advantage drops to 2.84%.
If forced to an answer in plain simple English, I would say the wheel shows evidence, but not proof beyond a reasonable doubt, that the wheel is biased. However, that bias is probably not enough to significantly and confidently overcome the house edge. Assuming the casino doesn't switch around the wheels among the tables, I would say that more data should be collected before betting large amounts of money. I'm sorry this answer is so noncommittal.
This question is raised and discussed in my forum at Wizard of Vegas.
Two players, Sam and Dan, each have five coins. Both must choose to place one to five coins in his hand. At the same time, each must reveal the number of coins played. If both choose the same number of coins, then Sam will win collect all coins played. If both choose different numbers of coins, then Dan will collect all coins played. Assuming both players are prefect logicians, what is the optimal strategy for Dan?
Dan should randomize his strategy as follows:
- Probability of picking one coin = 77/548.
- Probability of picking one coin = 107/548.
- Probability of picking one coin = 117/548.
- Probability of picking one coin = 122/548.
- Probability of picking one coin = 125/548.
With this strategy, Dan can expect to win 3.640510949 coins every turn, regardless of how many coins Sam picks.
A solution can be found in my Math Problems site, problem 230.
A related question, which led to this one, can be found in my forum at Wizard of Vegas.
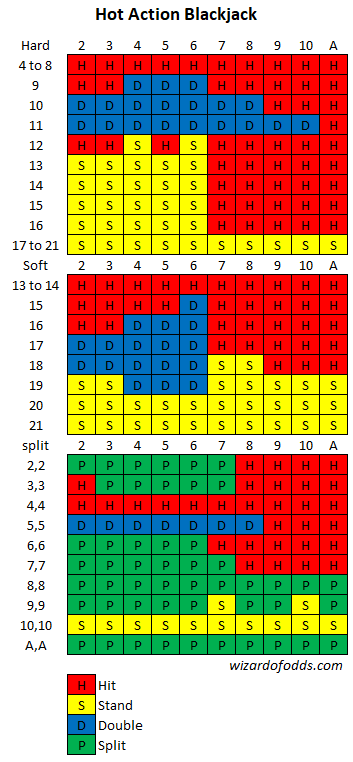
There is a blackjack game called Hot Action Blackjack being played at the California Grand Casino in San Francisco. The rules of the game are as follows:
- Six decks in a continuous shuffler with an additional 18 jokers with a face value of 2.
- Dealer hits soft 17.
- Double on any first 2 cards.
- Re-split up to four hands.
- No drawing to or re-splitting aces.
- No surrender.
- Blackjack pays 6 to 5.
- If the player's first two cards are jokers, then he gets a 4 to 1 bonus.
- If the player's first two cards are suited aces, then he gets a 5 to 1 bonus.
- Player must pay a 5% commission to play.
What is the basic strategy and house edge?
First, here is my basic strategy under these rules:
All things considered, I show a house edge of 6.01% (ouch!) based on the initial wager. In other words, if the player bet $100, not counting the $5 commission, then he could expect to lose $6.01. It goes to show why I would stay away from player-banked games in California, unless you're the one banking.
This question is raised and discussed in my forum at Wizard of Vegas.