Ask The Wizard #301
There is a prize draw at the local casino every week where the prize draw winner is offered $5,000 cash or the option to pick a mystery bag containing one of the following prizes:
- $2,000 cash
- $4,000 non-negotiable chips
- $6,000 non-negotiable chips
- $8,000 cash
- $10,000 cash
What would you choose and why?
First, I assume the "non-negotiable chips" are the use-till-you-lose type. These have a value of about 98% of face value, depending on the rules of the games you can use them on.
That said, the average bag is worth $5,960. That is almost 20% more than the cash offer. Even looking at it as a utility of money problem, you should still take a bag, even if you have no other wealth.
This question was asked and discussed in my forum at Wizard of Vegas.
What is the average number of draws you would need from a uniform distribution from 0 to 1 for the sum to equal 1?
What was the math problem on the chalkboard in the movie Good Will Hunting?
It was actually rather easy, especially for a course in combinatorial mathematics at MIT. Here is the wording of the problem:
"Draw all homeomorphically irreducible trees of size n=10."
Here is my attempt to put it in plain and simple English.
Using only straight lines, draw all figures where the sum of intersections and dead ends equals 10. You may not have any closed loops. You may also not have two equivalent figures. Any intersection must have at least three paths leading from it.
What do I mean by "equivalent," you might ask? It means you can move the pieces, while leaving the intersections alone, any way you wish and it won't create any new figures.
Here is an example:
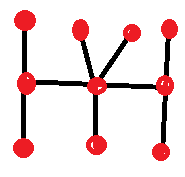
I'll give you a hint. Unlike the answer in the movie, there are ten of them. Will got only eight of them. See if you can match or beat Will Hunting.
- MATHEMATICS IN GOOD WILL HUNTING II: PROBLEMS FROM THE STUDENTS PERSPECTIVE -- Academic paper on the problem.
- THE GOOD WILL HUNTING MATH PROBLEM -- Discussion about the problem in my forum.
At certain casinos in Mexico they use dice instead of a wheel in roulette. Here are the rules:
- There are four dice -- two green, one red, and one blue.
- If the two green dice both land on one, then the outcome of the "spin" shall be a zero.
- If the two green dice both land on six, then the outcome of the "spin" shall be a double zero.
- If any other outcome occurs with the green dice, then the 36 possible outcomes of the red and blue dice shall be mapped to the numbers 1 and 36 to represent the "spin."
How does this change the odds compared to conventional roulette?
The probability of the 0 and 00 winning would be 1/36 each. If bets on these outcomes paid the usual 35 to 1, then the house edge would be exactly 0%.
The probability of any other number winning would be (34/36)*(1/36) = 2.62%. Compare that to 1/38=2.63% in conventional double-zero roulette. The house edge on any bet on the numbers 1 to 36 would be 5.56%. Compare that to the 5.26% in conventional double-zero roulette. My advice in this game would be to bet the zero and double-zero only.
If anyone can confirm or deny these rules and pays, please let me know.





