Ask The Wizard #259

For the benefit of other readers, at many casinos in Europe, if you make an even money bet in roulette and the ball lands in zero, then the wager becomes imprisoned. If the next roll would cause the wager to win, then it is returned without winnings. If the ball lands the opposite way, then the bet loses.

What happens to single-imprisoned bets if the ball lands in zero? If the casino allows only single imprisonment, then it would lose. However, some casinos allow for double imprisonment, which is what would happen. If a double imprisoned bet wins, then it returns to being single imprisoned. If the casino allows only up to double imprisonment, then a double imprisoned bet would lose on another zero. By the same logic, if a casino allows triple imprisonment, then a double imprisoned bet would become triple imprisoned on another zero.

The house edge under triple imprisonment is 1.370120%. Before I explain how I arrived at that, let’s do single and double imprisonment first. Assume the first bet is on red.

Let Z = probability of a zero = 1/37.
Let R = probability of a red number = 18/37.

Single imprisonment

pr(push) = ZR = 0.0131482834.
pr(win) = R = 0.4864864865.
pr(loss) = 1-pr(push)-pr(win) = 0.5003652301.
Expected value = pr(win)-pr(loss) = -0.0138787436.

Double imprisonment

The player will push if the first spin is a zero, then the player can repeat ZR from 0 to an infinite number of times, and then get a red. In other words, the ways to push are:

ZR, Z(ZR)R, Z(ZR)(ZR)R, Z(ZR)(ZR)(ZR)R, ...

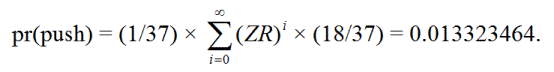
pr(push) = 0.013323464
pr(win) = 18/37 = 0.4864864865.
pr(loss) = 1-pr(push)-pr(win) = 0.5001900494.
Expected value = pr(win)-pr(loss) = -0.0137035629.

Triple imprisonment

First, let’s find the probability p₁ that a single imprisoned bet becomes triple imprisoned with two more zeros, and then eventually rises back up to being single imprisoned again. This can happen as follows:

ZZRR, ZZ(RZ)RR, ZZ(RZ)(RZ)RR, ZZ(RZ)(RZ)(RZ)RR, ...

In other words, the bet can bounce between triple and double imprisonment up to an infinite number of times.

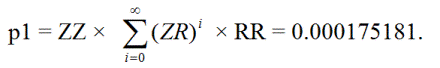
Second, let p₂ = the probability that a single imprisoned bet reaches the first or second level of imprisonment and then returns to single imprisonment.

let p₂ = ZR + p₁ = 0.013323464.

The player can repeat returning to the first level from zero to an infinite number of times. So the probability of a push is:

ZR + Z p₂R + Z p₂ p₂R + Z p₂ p₂ p₂R + ... =

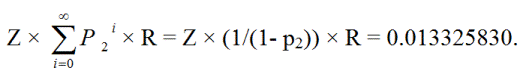
Z × (1/(1- p₂)) × R = 0.013325830.

pr(push) = 0.013325830.
pr(win) = 18/37 = 0.4864864865.
pr(loss) = 1-pr(push)-pr(win) = 0.5001876839.
Expected value = pr(win)-pr(loss) = -0.0137011974.

Infinite imprisonment

Not that you asked, Maff, but in Spain I hear they allow infinite imprisonment. Let p = probability of a push. This is also the probability of starting at level x of imprisonment, falling deeper in levels, but eventually climbing back up to x.

p = ZR + ZpR + ZppR + ZpppR + ...

p² - p + ZR = 0

By the Quadratic Formula p = (1-(1-4*RZ)^1/2)/2 = 0.0133258620.

pr(push) = 0.0133258620.
pr(win) = 18/37 = 0.4864864865.
pr(loss) = 1-pr(push)-pr(win) = 0.5001876515.
Expected value = pr(win)-pr(loss) = -0.0137011650.

Zeros ignored imprisonment

Finally, at some casinos zeros are simply ignored after the first zero which imprisons the bet. There the probability of a push is simply (1/37)×(1/2) = 0.0135135135.

The following table summarizes all four kinds of rules.

Imprisonment Odds

Imprisonment	Win	Push	Loss	Expected Value
Single	0.48648649	0.01314828	0.50036523	-0.01387874
Double	0.48648649	0.01332346	0.50019005	-0.01370356
Triple	0.48648649	0.01332583	0.50018768	-0.01370120
Infinite	0.48648649	0.01332586	0.50018765	-0.01370117
Zeros ignored	0.48648649	0.01351351	0.50000000	-0.01351351

I’d like to thank ChesterDog and weaselman for their mathematical help. I’d also like to give thanks and a plug to professor G. Artico and polarprof.it for the HTML of the summation formula above.

This question was raised and discussed in the forum of my companion site Wizard of Vegas.

7,281.8 coins. It is interesting to note that if you played only once at exactly that meter then the return would be 98.5% only. The reason you should play at that point is because of the assumption you are capable of playing until you pop the jackpot. That is like having a 2% cash back slot club. 98.5% + 2% = 100.5%.

I might add that if you start playing 4000-coin jackpot strategy at exactly a 7,281.8 jackpot, you can expect to profit 201.18 bets. However, if you took the time to learn the strategy changes for a 7,281.8 coin jackpot, then your expected profit would be 234.31 coins.

On a related note, I just finished reading The Secret World of Video Poker Progressives by Frank Kneeland. This book has lots of formulas for much more complicated progressive situations, as well as practical advice and stories based on his years running a team of progressive hunters. I recommend it for advantage progressive video poker players.

Stanford Wong address jokers in blackjack in his book Basic Blackjack. There he says each joker per deck is worth 4.2% to the player. So half a joker per deck would be worth 2.1%. His book contains a strategy for what card to declare the joker as, according to your other card(s), and the dealer’s up card.

This question was raised and discussed in the forum of my companion site Wizard of Vegas.

According to the September 2010 Current Blackjack Newsletter, there were 2099 blackjack tables in Las Vegas. The following table shows how many were the biggest four variations.

Blackjack Variants in Las Vegas

Game	Tables	Percent
6 to 5	467	22.2%
Blackjack Switch	42	2.0%
Super Fun 21	41	2.0%
Spanish 21	6	0.3%
Total	556	26.5%

This question was raised and discussed in the forum of my companion site Wizard of Vegas.