The Truth about Betting Systems

Introduction

Not only do betting systems fail to beat casino games with a house advantage, they can’t even dent it. Roulette balls and dice simply have no memory. Every spin in roulette and every toss in craps is independent of all past events. In the short run, you can fool yourself into thinking a betting system works, by risking a lot to win a little. However, in the long run no betting system can withstand the test of time. The longer you play, the ratio of money lost to money bet will get closer to the expectation for that game.

In the many years that run this site, I have received thousands of e-mails from believers in betting systems. Their faith surpasses religious levels. However, in all things, the more ridiculous a belief is the more tenaciously it tends to be held. Gamblers have been looking for a betting system that works for hundreds of years, and yet the casinos are still standing.

fail to beat casino games with a house advantage, they can’t even dent it

Ohio Recommended Online Casinos View All

Gambler's Fallacy

The biggest gambling myth is that an event that has not happened recently becomes overdue and more likely to occur. This is known as the “gambler’s fallacy.” Thousands of gamblers have devised betting systems that attempt to exploit the gambler’s fallacy by betting the opposite way of recent outcomes. For example, waiting for three reds in roulette and then betting on black. Hucksters sell “guaranteed” get-rich-quick betting systems that are ultimately based on the gambler’s fallacy. None of them work. If you don’t believe me here is what some other sources say on the topic:

A common gamblers’ fallacy called “the doctrine of the maturity of the chances” (or “Monte Carlo fallacy”) falsely assumes that each play in a game of chance is not independent of the others and that a series of outcomes of one sort should be balanced in the short run by other possibilities. A number of “systems” have been invented by gamblers based largely on this fallacy; casino operators are happy to encourage the use of such systems and to exploit any gambler’s neglect of the strict rules of probability and independent plays. — Encyclopedia Britannica (look under “gambling”)

No betting system can convert a subfair game into a profitable enterprise... — Probability and Measure (second edition, page 94) by Patrick Billingsley

The number of ‘guaranteed’ betting systems, the proliferation of myths and fallacies concerning such systems, and the countless people believing, propagating, venerating, protecting, and swearing by such systems are legion. Betting systems constitute one of the oldest delusions of gambling history. Betting systems votaries are spiritually akin to the proponents of perpetual motion machines, butting their heads against the second law of thermodynamics. — The Theory of Gambling and Statistical Logic (page 53) by Richard A. Epstein

Vegas Click also has a good expose of the gambler’s fallacy.

The Martingale

Every week I receive two or three emails asking me about the betting system by which a player doubles his/her bet after a loss. This system is generally played with an even money game such as the red/black bet in roulette or the pass/don’t pass bet in craps and is known as the Martingale. The idea is that by doubling your bet after a loss, you would always win enough to cover all past losses plus one unit. For example, if a player starts at $1 and loses four bets in a row, winning on the fifth, he will have lost $1+$2+$4+$8 = $15 on the four losing bets and won $16 on the fifth bet. The losses were covered and he had a profit of $1. The problem is that it is easier than you think to lose several bets in a row and run out of betting money after you’ve doubled it all away.

In order to prove this point, I created a program that simulated two systems, the Martingale and flat betting, and applied each by betting on the pass line in craps (which has a 49.29% probability of winning). The Martingale bettor would always start with a $1 bet and start the session with $255 which is enough to cover 8 losses in a row. The flat bettor would bet $1 every time. The Martingale player would play for 100 bets, or until he couldn’t cover the amount of a bet. In that case, he would stop playing and leave with the money he had left. In the event his 100th bet was a loss, he would keep betting until he either won a bet or couldn’t cover the next bet. The person flat betting would play 100 bets every time. I repeated this experiment for 1,000,000 sessions for both systems and tabulated the results. The graph below shows the results:

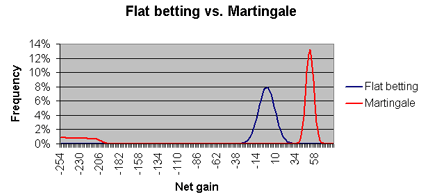
As you can see, the flat bettor has a bell curve with a peak at a loss of $1, and never strays very far from that peak. Usually the Martingale bettor would show a profit represented by the bell curve on the far right, peaking at $51; however, on the far left we see those times when he couldn’t cover a bet and walked away with a substantial loss. That happened for 19.65% of the sessions. Many believers in the Martingale mistakenly believe that the many wins will more than cover the few losses.

In this experiment, the average session loss for the flat bettor was $1.12, but was $4.20 for the Martingale bettor. In both cases, the ratio of money lost to money won was very close to 7/495, which is the house edge on the pass line bet in craps. This is not coincidental. No matter what system is used in the long run, this ratio will always approach the house edge. To prove this point consider the Martingale player on the pass line in craps who only desires to win $1, starts with a bet of $1, and has a bankroll of $2,047 to cover as many as 10 consecutive losses. The table below shows all possible outcomes with each probability, expected bet, and return.

The expected bet is the product of the total bet and the probability. Likewise, the expected return is the product of the total return and the probability. The last row shows this Martingale bettor to have had an average total bet of 11.81172639 and an average loss of 0.16703451. Dividing the average loss by the average bet yields .01414141. We now divide 7 by 495 (the house edge on the pass line) and we again get 0.01414141! This shows that the Martingale is neither better nor worse than flat betting when measured by the ratio of expected loss to expected bet. All betting systems are equal to flat betting when compared this way, as they should be. In other words, all betting systems are equally worthless.

Here is another experiment I conducted earlier which proves the same thing as the experiment above. This one is played against roulette testing three different systems. Player 1 flat bet a $1 each time. He was not using a betting system. Player 2 started a series of trials with a bet of $1 and increased his wager by $1 after every winning bet. A lost bet would constitute the end of a series and the next bet would be $1. Player 3 also started a series of bets with a bet of $1 but used a doubling strategy in that after a losing bet of $x he would bet $2x (the Martingale). A winning bet would constitute the end of a series and the next bet would be $1. To make it realistic I put a maximum bet on player 3 of $200. Below are the results of that experiment:

Player 1

• Total amount wagered = $1,000,000,000
• Average wager = $1.00
• Total loss = $52,667,912
• Expected loss = $52,631,579
• Ratio of loss to money wagered = 0.052668

Player 2

• Total amount wagered = $1,899,943,349
• Average wager = $1.90
• Total loss = $100,056,549
• Expected loss = $99,997,018
• Ratio of loss to money wagered = 0.052663

Player 3

• Total amount wagered = $5,744,751,450
• Average wager = $5.74
• Total loss = $302,679,372
• Expected loss = $302,355,340
• Ratio of loss to money wagered = 0.052688

As you can see the ratio of money lost to money wagered is always close to the normal house advantage of 1/19 ≈ 0.052632. In conclusion, varying of bet size depending on recent past wins or losses makes no difference in the long run outcome and is no different than always betting the same.

A Third Experiment

“An Old Timer’s Guide to Beating the Craps Table” was a betting system that makes big promises about turning the craps tables into your own personal cash register. I offered to test his system for free. Here are the results.

The Cancellation Betting System

Despite all my warnings about betting systems, readers continually ask me to suggest one. To satisfy those who enjoy playing systems I have done a full explanation and analysis of the cancellation betting system.

Don't Waste Your Money

The Internet is full of people selling betting systems with promises of beating the casino at games of luck. Those who sell these systems are the present day equivalent of the 19th century snake oil salesmen. Under no circumstances should you waste one penny on any gambling system. Every time one has been put to a computer simulation it failed and showed the same ratio of losses to money bet as flat betting. If you ask a system salesman about this you likely will get a reply such as, “In real life nobody plays millions of trials in the casino.” You’re likely to also hear that his/her system works in real life, but not when used against a computer simulation. It is interesting that professionals use computers to model real-life problems in just about every field of study, yet when it comes to betting systems computer analysis becomes “worthless and unreliable,” as the salesman of one system put it. In any event, such an excuse misses the point; the computer runs billions of trials simply to prove that a system is unsound. If it won’t work on a computer, it won’t work in the casino.

Gambling systems have been around for as long as gambling has. No system has ever been proven to work. From an inside source, I know that system salesmen go from selling one kind of system to another. It is a dirty business by which they steal ideas from each other, and are always attempting to rehash old systems as something new.

System salesmen usually promise ridiculous advantages. For example, even with just a 1% advantage on an even money bet, it would not be difficult to parlay $100 into $1,000,000 by betting in proportion to bankroll. I was asked to prove this claim so I wrote a computer simulation based on the toss of a biased coin, with a 50.5% chance of winning. At all times the player bet 1% of his bankroll, rounded down to the nearest dollar. However, if a winning bet would put the player over $1,000,000 then he only bet as much as he needed to get to exactly $1,000,000. In addition, I ran simulations with a 2% advantage and for a starting bankroll of $1,000. Following are the results of all four tests.

$100 Bankroll, 1% Advantage

• Bets won = 7,182,811,698 (50.4999%)
• Bets lost = 7,040,599,544 (49.5001%)
• Player achieved $1,000,000 first = 79,438 (83.019%)
• Player went bust first = 16,249 (16.981%)
• Average number of bets to reach $1,000,000 = 174,972 (364.5 days at 8 hours per day, 60 bets per hour)

$100 Bankroll, 2% Advantage

• Bets won = 7,027,117,205 (51.0000%)
• Bets lost = 6,751,539,769 (49.0000%)
• Player achieved $1,000,000 first = 215,702 (98.099%)
• Player went bust first = 4,180 (1.901%)
• Average number of bets to reach $1,000,000 = 63,775 (132.9 days at 8 hours per day, 60 bets per hour)

$1,000 Bankroll, 1% Advantage

• Bets won = 5,213,026,190 (50.4999%)
• Bets lost = 5,109,817,544 (49.5001%)
• Player achieved $1,000,000 first = 74,818 (99.0285%)
• Player went bust first = 734 (0.9715%)
• Average number of bets to reach $1,000,000 = 137,208 (285.8 days at 8 hours per day, 60 bets per hour)

$1,000 Bankroll, 2% Advantage

• Bets won = 6,332,837,070 (50.9996%)
• Bets lost = 6,084,596,671 (49.0004%)
• Player achieved $1,000,000 first = 267,445 (99.9996%)
• Player went bust first = 1 (0.0004%)
• Average number of bets to reach $1,000,000 = 46,428 (96.7 days at 8 hours per day, 60 bets per hour)

These simulations prove that with just a small advantage of as little as 1% and a bankroll of as little as $100 you can grind your way to a million dollars through the gambling equivalent of compound interest. Yet you never hear of this actually happening. Could it be that these gambling systems don’t work after all?!

Here are some examples of system salesmen who try to take advantage of the mathematically challenged. There are hundreds of sites like these on the Internet, and this list is just a sampling. Frequently these sites vanish in the middle of the night, or suddenly direct traffic to a porn site. Please do let me know if any of these links don’t work or take you to other than the intended place.

• Let’s Talk Winning
• Power Craps
• Goldmine Roulette

Also, be warned that there are many others out there selling get rich quick gambling schemes that claim they are not betting systems. These sites usually throw out lots of fancy physics words like “chaos” and “fractals,” but display no evidence they know what these words mean. In the past, I have listed some such sites above but got angry letters claiming I shouldn’t criticize what I don’t understand. Personally, I feel that every method claiming an easy way to beat the casinos is a scam, and I don’t need to understand whatever the secret is. However, to be totally fair, I’ll only list betting systems above since those have been mathematically debunked by computer simulations. If anyone did find a truly easy way to beat the casinos, why aren’t they getting rich doing it?

The Wizard of Odds Challenge

For about six years, from 1999 to 2005, I offered $20,000 to anyone with a betting system that could show a profit over a one billion hand computer simulation. Here you can find the rules of the challenge. However, in all this time I only had one serious taker and hundreds of people wasting my time, pretending to be interested but never following through. So in January 2005, I took down the offer.

My webmaster, Michael Bluejay, now offers essentially the same challenge on his own site, VegasClick.com. If you accept his challenge, and win, I will be happy to state as such on the front page of this site, for proving the experts wrong.

A Fourth Experiment

On October 19, 2004, Daniel Rainsong accepted my challenge. Mr. Rainsong was so confident he would win he doubled the stakes to my $40,000 against his $4,000. Although the rules of the challenge are based on craps or roulette I allowed this challenge to be based on blackjack rules with a house edge of only 0.26%. Can a betting system beat a game with a house edge this small and a 1,028 bet spread? Visit my Rainsong Challenge page for all the details.

Please, Don't Write

I no longer respond to e-mails that suggest a player can beat a negative expectation game over the long run with a betting system. Such e-mail is deleted on sight. I have said all I have to say on the topic here and in my Gambling FAQ.

If you really want to discuss the topic, then I invite you not to do so at my forum at Wizard of Vegas, but instead one where you will be among like-minded people, like the forum atJohn Patrick's site (Update: This site has, not surprisingly, gone the way of the dodo bird).

 

Internal Links

• Oscar's Grind betting system.
• Labouchere betting system.
• Fibonacci betting system.
• Martingale betting system.
• Anti-Martingale betting system.
• D'Alembert betting system.
• Keefer roulette system.
• 1-3-2-6 Betting System.
• 2-1-2 (Manhattan) Betting System.
• Three Point Molly Betting System.
• Three Point Dolly Betting System.
• Rothstein Betting System.

Related Reading

• The Online Advantage (When the Player Has the Edge)
• Quarterly Online Casino Bonuses and Online Tips
• Casino Bonuses, Terms, Playthrough & What it Means for Players (House Edge Calculator)
• Real Casinos, Real Money
• Guide to No-Deposit Bonuses

External Links

• Betting Systems and the House Edge, an article by Ph.D. mathematician Eliot Jacobson debunking betting systems.
• Betting Systems, an article by Michael Bluejay of VegasClick.
• Debunking the “No Risk Don’t Come” betting system.

Written by: Michael Shackleford