On this page
Dice Probability
On this page
Introduction
Before you play any dice game it is good to know the probability of any given total to be thrown. First lets look at the possibilities of the total of two dice. The table below shows the six possibilities for die 1 along the left column and the six possibilities for die 2 along the top column. The body of the table shows the sum of die 1 and die 2.
Two Dice Totals
| Die 1 | Die 2 | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
The colors of the body of the table illustrate the number of ways to throw each total. The probability of throwing any given total is the number of ways to throw that total divided by the total number of combinations (36). In the following table the specific number of ways to throw each total and the probability of throwing that total is shown.
| Total | Number of Combinations |
Probability |
|---|---|---|
| 2 | 1 | 2.78% |
| 3 | 2 | 5.56% |
| 4 | 3 | 8.33% |
| 5 | 4 | 11.11% |
| 6 | 5 | 13.89% |
| 7 | 6 | 16.67% |
| 8 | 5 | 13.89% |
| 9 | 4 | 11.11% |
| 10 | 3 | 8.33% |
| 11 | 2 | 5.56% |
| 12 | 1 | 2.78% |
| Total | 36 | 100% |
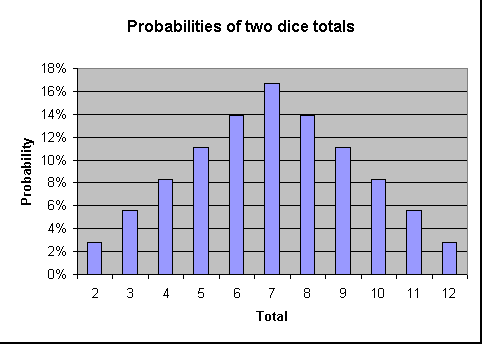
The following shows the probability of throwing each total in a chart format. As the chart shows the closer the total is to 7 the greater is the probability of it being thrown.
Online Craps Casino Bonuses View All
Bonus Code
Same for Blackjack
- 60 times on Slots
- 120 times on Poker, Roulette
- 240 times on Baccarat
- 600 times on Video Poker
The Field Bet Example
Now that we understand the probability of throwing each total we can apply this information to the dice games in the casinos to calculate the house edge. For example consider the field bet in craps. This bet pays 1:1 (even money) if the next throw is a 3, 4, 9, 10, or 11, 2:1 (double the bet) on the 2, and 3:1 (triple the bet) on the 12. Note that there are 7 totals that win and only 4 that lose which might cause someone who didn't know better to think it was a good gamble.
The player's return can be defined as the sum of the products of the probability of each event and the net return of that event. The following table shows each possible total, the net return, the probability of throwing that total, and the average return. The average return is the product of the net return and the probability. The player's return is the sum of the average returns.
| Total | Net Return | Probability | Average Return |
|---|---|---|---|
| 2 | 2 | 0.0278 | 0.0556 |
| 3 | 1 | 0.0556 | 0.0556 |
| 4 | 1 | 0.0833 | 0.0833 |
| 5 | -1 | 0.1111 | -0.1111 |
| 6 | -1 | 0.1389 | -0.1389 |
| 7 | -1 | 0.1667 | -0.1667 |
| 8 | -1 | 0.1389 | -0.1389 |
| 9 | 1 | 0.1111 | 0.1111 |
| 10 | 1 | 0.0833 | 0.0833 |
| 11 | 1 | 0.0556 | 0.0556 |
| 12 | 3 | 0.0278 | 0.0834 |
| Total | 1 | -0.0278 |
The last row shows the player's return to be -.0278, in other words for every $1 bet the player can expect to lose 2.78 cents. The player's loss is the house's gain so the house edge is the product of -1 and the player's return, in this case 0.0278 or 2.78%.
For the probabilities in the sum of more than two dice please see my probabilities for 1 to 25 dice section.
Ohio Recommended Online Casinos
View All
UP TO $11,000 BONUS
All US players welcome
Over 200 casino games
Play on PC or Mobile
UP TO $3000 BONUS
Casino & Sportsbook
American players only
Play on desktop or mobile
UP TO 777$ BONUS
Large welcome bonus
Daily casino tournaments
Popular games