Probability - Dice
If you are rolling 6 six-sided standard dice what are the odds of rolling six of a kind?
The answer is 6*(1/6)6 = 6/46,656 = 1/7,776 =~ 0.0001286 .
What is the average number of rolls until a shooter "sevens out"? I know that a 7 will appear every 6 rolls, but with come-out 7-11s and craps, plus the possibility of shooters making multiple points, I think the average number of rolls may be higher than expected. Is there any mathematical reference material on this?
The average number of rolls per shooter is 8.525510. For the probability of exactly 2 to 200 rolls, please see my craps probability of survival page.
What are the odds (and frequency) in 100,000 rolls of the dice (craps/dont pass line) of losing a DP bet 2x’s.3x’s 4x’s 5x’s 6x’s 7x’s 8x’s or 9x’s in a row.
My craps appendix shows how to work out the odds for any one bet. There you will see the probability of losing the don’t pass bet is 2928/5940. The probability of losing n bets in a row is (2928/5940)n. The frequency in 100,000 of losing exactly n can be closely approximated as 100,000 * (2928/5940)n+2.
What are the odds of rolling the same number with six dice in one roll?
The odds of getting six of the same number with six dice is 6*(1/6)6=1/7776 =~ 0.01286%.
How often can you roll a pair of dice 28 times without getting a 7? How do you figure this? Congratulation on your site, it’s great.
Thanks for the compliment. I take it you mean what is the probability of rolling a pair of dice 28 times without getting a 7. The probability of not rolling a 7 on any one roll is 5/6. The probability of not rolling a 7 in 28 rolls is (5/6)28 = 0.006066, or about 1 in 165.
Just a question about an Oriental dice game, where the players are supposed to guess which side of the die shows up. The players will first place their bets on 1,2,3,4,5,6 (like roulette) and then the "dealer" will roll 3 dice simultaneously. Payouts are 1:1 if the chosen numbers shows up once (on any of the 3 dice), 2:1 if the chosen no shows up twice, and 3:1 if the chosen number appears on all 3 dice. As the player can place any number of bets of the board, what will be the optimum number of bets to place? (assuming all my bets are equal in size)
The probability of three matching is 1/216. The probability of two matching is 3*5/216. The probability of one matching is 25*5/216. The probability of 0 matching is 5*5*5/216. So the expected return is 3*(1/216)+2*(15/216)+1*(75/216)-1*(125/216)=-17/216=-7.87%. There is no optimal number of bets, you will give up an expected 7.87% of total money bet no matter what you do.
These bets can be made in both sic bo and chuck a luck.
Mr. Wizard, what is the probability of rolling two pair when rolling four dice?
There are combin(6,2)=15 different sets of pairs possible. There are combin(4,2)=6 ways the dice can roll any specific two pair. There are 6^4=1296 ways to roll four dice. So the probability is 90/1296=6.9444%.
If I roll a die, my probability of rolling a six is 1/6. If I roll two dice, does my probability of rolling a six on one of them increase, or does it stay at 1/6?
If you rolled x dice the probability of getting at least one 6 is 1-(5/6)2. In the case of two dice this is 30.56%.
How many different ways are there of rolling 3 ones using 6 dice?
First there are combin(6,3)=20 ways you can choose three dice out of 6 for the three ones. Then each of the other three can be any of five numbers. So, the total ways are 20×53=2500. The total number of ways to throw all the dice are 66=46,656, so the probability of rolling exactly three ones is 2500/46656=0.0536. For help with the combin function see my probabilities in poker section.
What is the probability of any one die showing ONE when 3 dice are throw together. My understanding is it should be 50% chance (1/6+1/6+1/6=1/2 -->50%) But in your odds table it shown 34.72%. Please help.
The probability of rolling exactly one one with three dice is 3*(5/6)2*(1/6) = 75/216 = 34.72%.
What is the probability of rolling a "pair" when tossing 4 dice?
The pair can be any one of 6 numbers. The other two singletons can be among the other five. So there are 6*combin(5,2)=60 combinations already. There are combin(4,2)=6 combinations of dice on which the pair can appear. The two singletons can be arrange in two ways. So there are 60*12=720 ways to throw a pair. The total number of all ways to throw the dice is 64=1296. So the probability is 720/1296 =~ 55.56%.
My friend owns a bar and has a "shake of the day" where there are ten dice in a Tupperware container, what are the odds of matching 8 out of the 10 in one shake. Thank you for your time.
The probability that if you roll 10 dice and exactly 8 numbers are the same is 6*combin(10,8)*(1/6)8*(5/6)2 = 1/8957.952. The probability of matching at least 8 is 6*[combin(10,8)*(1/6)8*(5/6)2 + combin(10,9)*(1/6)9*(5/6) + (1/6)10] = 1/8569.469.
I recently rolled, during a game of backgammon, double sixes four consecutive times. What are the odds of this happening again?
With every new roll the probability the next four rolls will be all double sixes is (1/36)4 = 1 in 1679616.
What is the probability of getting a straight by a single throw of 5 dice?
There are two possible spans: 1 to 5 and 2 to 6. Each of these spans can be ordered in 5!=120 ways. There are 65 = 7776 ways to roll five dice. So the probability is 2*120/7776 = 3.09%. The probability of this seems to be much higher right after I put mark 0 for large straight during a game of Yahtzee.
A fair sided die is rolled 30 times. What is the expected number of times that number 1 will come up? What is the probability that number 1 will come up it’s expected number of times?
The expected number of ones is 30*(1/6) = 5. The probability of exactly 5 ones is combin(30,5)*(1/6)5*(5/6)25 = 19.21%.
If I have any give number of dice what is the probability that if I roll them all of them at least one will land on a one?
The probability that all the dice will not be a one is (5/6)n. So the probability of at least one 1 is 1-(5/6)n. Let’s take an example of five dice. The answer would be 1-(5/6)5 = 59.81%.
If I throw 36 dice what is the probability of getting at least one six?
1-(5/6)36 = 99.86%
If I kept throwing and removed all the sixes each time, how would I predict the theoretical number of dice remaining after a particular number of throws?
Each roll the expectation is that 5/6 of the dice will remain. So the expected number of dice remaining after n throws would be 36*(5/6)n. For example after 10 throws you would have 5.81 dice left, on average.
If I roll three dice, what is the probability of getting at least two numbers the same?
The probability all numbers will be different is (5/6)*(4/6)=20/36. So the probability at least two numbers will be the same is 1-(20/36) = 16/36 = 44.44%.
If two people throw a pair of dice, What is the probability that it is the same number? Is there a formula to figure this out?
Yes. You simply run through all total from 2 to 12 and determine the probability of rolling each twice. So the answer would be (1/36)2+(2/36)2+(3/36)2+(4/36)2+(5/36)2+(6/36)2+(5/36)2+(4/36)2+(3/36)2+(2/36)2+(1/36)2 = 11.27%.
I recently attended a hospital fete. There was a new car as a prize if 7 dice produced 7 sixes in one throw. £1.00 a go. Odds on this must be high but how high?
The probability of throwing seven sixes with seven dice is (1/6)7 = 1 in 279,936. So the car would have to have a value of £279,936 or more for this to be a good bet. Even your average Rolls Royce is not worth this much, so I would say that was a terrible bet.
[Bluejay adds: Uh, yeah, but I think the point was that it was for charity. What’s more fun: Donating £1.00 to charity and getting nothing back but the good feeling of helping out, or donating £1.00 and getting the good feeling plus the longshot chance of winning a car?]
What are the probabilities for a 5 of a kind, 4 of a kind, 3 of a kind, full house, 2 pair, pair, straight, and nothing with the roll of five dice?
- Five of a kind: 6/65 = 0.08% (obvious)
- Four of a kind: 5*6*5 = 1.93% (five possible positions for the singleton * 6 ranks for the four of a kind * 5 ranks for the singleton).
- Full house: combin(5,3)*6*5/65 = 3.86% (combin(5,3) positions for the three of a kind * 6 ranks for the three of a kind * 2 ranks for the pair).
- Three of a kind: COMBIN(5,3)*COMBIN(2,1)*6*COMBIN(5,2) / 65 = 15.43%. (combin(5,3) positions for the three of a kind * combin(2,1) positions for the larger of the singletons * 6 ranks of the three of a kind * combin(5,2) ranks for the two singletons.
- Two pair: COMBIN(5,2)*COMBIN(3,2)*COMBIN(6,2)*4 / 65 = 23.15% (combin(5,2) positions for the higher pair * combin(3,2) positions for the lower pair * combin(6,4) ranks for the two pair * 4 ranks for the singleton.
- Pair: COMBIN(5,2)*fact(3)*6*combin(5,3) / 65 = 46.30% (combin(5,2) positions for the pair * fact(3) positions for the three singletons * 6 ranks for the pair * combin(5,3) ranks for the singletons.
- Straight: 2*fact(5) / 65 = 3.09% (2 spans for the straight {1-5 or 2-6} * fact(5) ways to arrange the order).
- Nothing: ((COMBIN(6,5)-2)*FACT(5)) / 65 = 6.17% (combin(6,5) ways to choose 5 ranks out of six, less 2 for the straights, * fact(5) ways to arrange the order.
Hi Wizard, I wanted to know if you can answer this. In a popular gambling game in 17th century France, a player would roll a pair of dice 24 times. He would win his bet if at least one of these rolls was a double six. There was a debate at the time over whether the probability of winning was above or below an even 50%. Can you help me?
Sure, this is easy. The probability of rolling at least one 12 in 24 rolls is 1-(35/36)24 = 49.14%. So the odds favor betting against a 12. This is a clever bet because the expected number of twelves in 24 rolls is 2/3. However that does not mean the probability of a 12 is 2/3, because sometimes there will be more than one 12, and the player betting on 12 doesn’t win any more for extra twelves after the first one. If the probability of winning any given trial is p, the number of trials is n, and the probability of at least one win is w then solving for n in terms of p and w gives us...
w=1-(1-p)n
1-w = (1-p)n
log(1-w) = log((1-p)n)
log(1-w) = n*log(1-p)
n= log(1-w)/log(1-p)
So in your example n = log(1-.5) / log(1-(1/36)) = log(0.5) / log(35/36) = 24.6051. So if the probability of success is 50% in 24.6 rolls it must be slightly less in 24 rolls.
What is the probability of rolling 1,2,3,4,5,6 with six dice, six times in a row?
The probability of rolling 123456 with six dice in a single roll can be expressed as prob(second die does not match first die) * prob(third die does not match first or second die) * ... = 1*(5/6)*(4/6)*(3/6)*(2/6)*(1/6) = 0.015432. So the probability of doing this six times in a row is 0.0154326 = 1 in 74,037,208,411.
If I roll a single die 6 times, what is the probability of getting a "2" exactly 4 times?
Combin(6,2)*(1/6)4*(5/6)2 = 0.008037551.
What is the probability of rolling 13 or more with 3, 4, and 5 dice, if you are allowed to keep the highest three dice in your roll?
Here are the probabilities:
3 dice: 25.93%
4 dice: 48.77%
5 dice: 66.13%.
Suppose we roll three fair six-sided dice. What’s the conditional probability that the first dice shows 4, given that the sum of the three numbers showing is 12?
The probability of A given B is the probability of A and B divided by the probability of B. In this case the probability of rolling a 4 on the first die and then a total of 8 on the other two is (1/6)*(5/36) = 5/216. The probability of rolling any total of 12 with 3 dice is 25/216, as shown in my sic bo section. So the answer is (5/216)/(25/216) = 5/25 = 20%.
In a recent programming exercise myself and other students were asked to describe a six-sided die in code, and then use our dice to determine play simple game. The object of the game was to roll the dice until the sum of the tosses reached exactly 100. Any toss that put the total over 100 would not be added and merely added to statistics. Quickly it was determined that 17 throws would be the least amount of throws needed to reach 100. However calculating the odds of that occurring has proved elusive. Calculating the odds of a specific sequence of throws is rather straight forward, but how might one factor in both non-specific ordering of throws, and the different ways of reaching 100 in 17 throws (16*6 + 1*4 and 15*6 + 2*5)?
The two ways you mention are the only ways to throw a total of 100 in 17 throws. The probability of throwing 16 sixes and one four is 17*(1/6)17. There are 17 possible positions of the 4 and each sequence has a probability of (1/6)*(1/6)*...*(1/6) with 17 terms. The number of ways to get 15 sixes and 2 fives is combin(17,2) = 136. So the probability of 15 sixes and 2 fives is 136*(1/6)17. So the total probability is (17+136)*(1/6)17. = 1 in 110,631,761,077.
There are 3 dice, 2 are proper six sided dice, while one is a die with all sides containing a six. All the dice are in my pocket. I randomly take out a die and throw it. The result is a 6. What is the probability that the die was one of the proper dice with 6 different values?
Let A = Choosing the normal die
Let B = Rolling a 6 with randomly chosen die
Answer = Pr(A given B) = Pr(A and B)/pr(B) = ((2/3)*(1/6))/((2/3)*(1/6)+(1/3)*1) = (2/18)/((2/18)+(6/18)) = 1/4.
If you can roll six dice only once, what is the probability of rolling 6,6,6,6,1, and 4 in any order?
There are 6!/(4!*1!*1!) = 30 ways to arrange these numbers in any order. Another way to look at it is there are 6 positions to put the 1, and 5 left to put the 4, so 6*5=30. The probability of getting 666614 in exactly that order is 1 in 66 = 1 in 46656. Multiply that by 30 for the 30 possible orders and the answer is 30/46656 = 0.0643%, or 1 in 1552.2.
My understanding of "wait time" for an event is the reciprocal of the probability of that event. I’m interested in calculating the wait time to roll consecutive 2s using one die. In a simulation I get 42 rolls on average. How do I make the connection with the probability of rolling consecutive 2s?
It is true that for single events if the probability is p then the average wait time is 1/p. However it gets more complicated with consecutive events. Let x be the state that the last roll was not a two. This is also the state at the beginning. Let y be the state that the last roll was a two. After the first roll there is a 5/6 chance we will still be in state x, and 1/6 chance we will be in state y. Let Ex(x) be the expected number of rolls from state x, and Ex(y) the expected number from state y. Then...
Ex(x) = 1 + (5/6)*ex(x) + (1/6)*ex(y), and
Ex(y) = 1 + (5/6)*ex(x)
Solving for these two equations...
Ex(x) = 1 + (5/6)*ex(x) + (1/6)*( 1 + (5/6)*Ex(x))
Ex(x) = 7/6 + (35/36)*Ex(x)
(1/36)*Ex(x) = 7/6
Ex(x) = 36*(7/6) = 42
So the average wait time for two consecutive twos is 42 rolls.
I have the same type of problem, only the expected flips to get two heads, in my site of math problems, see problem 128.
Can you tell me the odds of rolling two of the same number with two dice, three dice, and four dice? I am wondering how many dice would one have to roll at one time so that the odds are on the side of the person rolling the dice. (It does not make any difference which number is doubled.)
Here is the probability of getting at least one number more than once according to the number of rolls:
Probability of a Pair or More
| Rolls | Probability |
| 2 rolls | 16.67% |
| 3 rolls | 44.44% |
| 4 rolls | 72.22% |
| 5 rolls | 90.74% |
| 6 rolls | 98.46% |
What is the chance of getting a sum over 100, when rolling 20 dice? Kind regards
I started to use the Normal approximation to solve this, but the probability of over 100 points is too low for that method to be accurate. So I did a random simulation of 8.25 million trials and the number of trails that were 101 points or more was 127. So the probability is about 1 in 65,000.
Wizard, could you please describe the equivalent odds of the California SuperLotto Plus (1 in 41.4 Million), in terms of number of consecutive times of rolling 7 or 11? I heard it somewhere before. Most people cannot comprehend the lottery odds. But, the rolling of dice -- they can relate.
Let n be your answer. The probability of rolling a 7 or 11 is 8/36. To solve for n:
(8/36)n = 1/41,400,000
log((8/36)n) = log(1/41,400,000)
n × log(8/36) = log(1/41,400,000)
n = log(1/41,400,000)/log(8/36)
n = -7.617 / -0.65321
n = 11.6608
So there you go, the probability of hitting the SuperLotto is the same as rolling a seven or eleven 11.66 times in a row. For those who can’t comprehend a partial throw I would rephrase as the probability falls between 11 and 12 consecutive rolls.
We are in a disagreement between workers. there is a bar down the street that has a shake a day. which is you must throw five dice at once and all five must end up being the same "like yahtzee" but he gives you three chance at it. but you must pick up all the dice all three times. so the questions is what’s the odds to do it in one shake and what’s the odds to do it in the three shakes allowed. Thanks , if you already answered this before i am sorry but i couldt find it.
The probability of a five-of-a-kind on one throw is 6*(1/6)5 = 1/1,296. This is because there are six different five-of-a-kinds (one to six) and the probability each die will be that number is (1/6). The probability of not getting a five-of-a-kind is 1-(1/1,296)=1,295/1,296. The probability of going three attempts without a three of a kind is (1,295/1,296)3=99.77%. So the probability of getting at least one five-of-a-kind in three tries is 100%-99.77% = 0.23%.
What is the expected number of tosses required in order to obtain at least one of each of the possible outcomes on an unbiased 6 sided dice?
If the probability of something is p then on average it will take 1/p trials for it to happen the first time. Obviously, on the first roll you’ll cross off one number. The probability of rolling one of the other five numbers next is 5/6. So it will take on average 1/(5/6)=6/5=1.2 rolls for that to happen. Following that reasoning to the end, the expected number of rolls is (6/6)+(6/5)+(6/4)+(6/3)+(6/2)+(6/1) = 14.7.
What is the classical probability of getting a total of 12 when 5 balanced dice are rolled?
I hope you’re happy, I just added a new section answering questions such as this for 1 to 25 dice. As the five-dice table shows, the probability of rolling a total of 12 is 0.039223251028807.
If two dice are rolled over and over, until either of the following events happen, then which is more likely to happen first:
- A total of six and eight is rolled, in either order, with duplicates allowed.
- A total of seven is rolled twice.
Somebody offered me a bet that that the six and eight would occur first. I accepted because seven is the most likely total. However, I lost $2,500 doing this over and over. What are the odds?
I’m afraid you had the square side of this bet. The probability of rolling two sevens before a six and eight is 45.44%. Here are all the possible outcomes. The first column is the order of petintent rolls to the outcome of the bet, ignoring all others.
Two Sevens before Six and Eight Bet
| Relavant Rolls | Probability | Formula | Outcome |
| 6,8 | 0.142045 | (5/16)*(5/11) | Lose |
| 8,6 | 0.142045 | (5/16)*(5/11) | Lose |
| 6,7,8 | 0.077479 | (5/16)*(6/11)*(5/11) | Lose |
| 7,6,8 | 0.053267 | (6/16)*(5/16)*(5/11) | Lose |
| 8,7,6 | 0.077479 | (5/16)*(6/11)*(5/11) | Lose |
| 7,8,6 | 0.053267 | (6/16)*(5/16)*(5/11) | Lose |
| 7,7 | 0.140625 | (6/16)*(6/16) | Win |
| 6,7,7 | 0.092975 | (5/16)*(6/11)*(6/11) | Win |
| 8,7,7 | 0.092975 | (5/16)*(6/11)*(6/11) | Win |
| 7,6,7 | 0.06392 | (6/16)*(5/16)*(6/11) | Win |
| 7,8,7 | 0.06392 | (6/16)*(5/16)*(6/11) | Win |
Basically, the reason the 6 and 8 is the better side is you can hit those numbers in either order: 6 then 8, or 8 then 6. With two sevens there is only one order, a 7 and then another 7.
Two questions, please: 1) What is the probability of rolling 6,6,6,6,6,6 @ one time, with (6)6-sided die? 2)What is the probability of rolling 1,2,3,4,5,6 @ one time with (6) 6-sided die? Thanks! It’s killing me!
The probability of six sixes is (1/6)6 = 1 in 46656. The probability of rolling 1,2,3,4,5,6 with six dice is 6!/66 = 1 in 64.8
What is the probability of getting any given number more than once if you roll a die ten times?
1-(5/6)10-10 × (1/6) × (5/6)9 = 51.55%.
In a game called Taxation and Evasion, a player rolls a pair of dice. On any roll if the sum is 7,11, or 12, the player gets audited; any other sum they avoid taxes. If a player rolls the pair 5 times, what is the probability that he avoids taxes?
The probability of a 7, 11, or 12 is (6+2+1)/36 = 9/36 = 1/4. See my section on dice probability basics for how I arrived at that figure. The probability of rolling anything else is 3/4. The probability of going five rolls without rolling a 7, 11, or 12 is (3/4)5 = 23.73%.
How many throws of a die does it take before it is likely that you have thrown a 1, 2, 3, 4, 5, and 6 at least once each? Any ideas on generalizing this for an n-sided die?
Not that you asked, but let me address the mean first. For a six-sided die, the expected number of throws to get each face at least once is (6/6)+(6/5)+(6/4)+(6/3)+(6/2)+(6/1) = 14.7. For an n-sided die the expected throws is (n/n) + (n/(n-1)) + (n/(n-2)) + ... + n. The median number of throws required is 13. The probability of taking 13 rolls or less is 51.4%, and 13 rolls or more is 56.21%.
I know you’re skeptical of dice control. I have been practicing dice setting and controlled shooting for 3 months. What is the probability of throwing 78 sevens over 655 throws randomly? Thanks for the help :)
For large numbers of throws we can use the Gaussian Curve approximation. The expected number of sevens in 655 throws is 655 × (1/6) = 109.1667. The variance is 655 × (1/6) × (5/6) = 90.9722. The standard deviation is sqr(90.9722) = 9.5379. Your 78 sevens is 109.1667 − 78 = 31.1667 less than expectation. This is (31.1667 - 0.5)/9.5379 = 3.22 standard deviations below expectation. The probability of falling 3.22 or more standard deviations south of expectations is 0.000641, or 1 in 1,560. I got this figure in Excel, using the formula, normsdist(-3.22).
This is about controlling the dice at Craps. You previously discussed the Stanford Wong Experiment, stating, "The terms of the bet were whether precision shooters could roll fewer than 79.5 sevens in 500 rolls of the dice. The expected number in a random game would be 83.33. The probability of rolling 79 or fewer sevens in 500 random rolls is 32.66%.... The probability of rolling 74 or fewer sevens in 500 random rolls is 14.41%."
The question I have about this bet is that 14.41% still isn’t "statistically significant" [ i.e. p < 0.05 ] , which is usually taken to mean greater than two Standard Deviations from the Mean -- or a probability of less than a *combined* 5% of the event happening randomly on EITHER end of the series.
How many Sevens would have to be rolled in 500 rolls before you could say that there is a less than 2.5% chance that the outcome was entirely random (i.e. that the outcome was statistically significant) ?
Many Thanks & BTW , yours is ABSOLUTELY the BEST web site on the subject of gambling odds & probabilities that I’ve found .... keep up the good work !!!
Thank you for the kind words. You should not state the probability that the throws were non-random is p. The way it should be phrased is the probability that a random game would produce such a result is p. Nobody expected 500 rolls to prove or disprove anything. It wasn’t I who set the line at 79.5 sevens, but I doubt it was chosen to be statistically significant; but rather, I suspect the it was a point at which both parties would agree to the bet.
The 2.5% level of significance is 1.96 standard deviations from expectations. This can be found with the formula =normsinv(0.025) in Excel. The standard deviation of 500 rolls is sqr(500*(1/6)*(5/6)) = 8.333. So 1.96 standard deviations is 1.96 * 8.333 = 16.333 rolls south of expectations. The expected number of sevens in 500 throws is 500*(1/6) = 83.333. So 1.96 standard deviations south of that is 83.333 − 16.333 = 67. Checking this using the binomial distribution, the exact probability of 67 or fewer sevens is 2.627%.
What is the expected number of rolls needed to get a Yahtzee?
Assuming the player always holds the most represented number, the average is 11.09. Here is a table showing the distribution of the number of rolls over a random simulation of 82.6 million trials.
Yahtzee Experiment
| Rolls | Occurences | Probability |
| 1 | 63908 | 0.00077371 |
| 2 | 977954 | 0.0118396 |
| 3 | 2758635 | 0.0333975 |
| 4 | 4504806 | 0.0545376 |
| 5 | 5776444 | 0.0699327 |
| 6 | 6491538 | 0.0785901 |
| 7 | 6727992 | 0.0814527 |
| 8 | 6601612 | 0.0799227 |
| 9 | 6246388 | 0.0756221 |
| 10 | 5741778 | 0.0695131 |
| 11 | 5174553 | 0.0626459 |
| 12 | 4591986 | 0.0555931 |
| 13 | 4022755 | 0.0487016 |
| 14 | 3492745 | 0.042285 |
| 15 | 3008766 | 0.0364257 |
| 16 | 2577969 | 0.0312103 |
| 17 | 2193272 | 0.0265529 |
| 18 | 1864107 | 0.0225679 |
| 19 | 1575763 | 0.019077 |
| 20 | 1329971 | 0.0161013 |
| 21 | 1118788 | 0.0135446 |
| 22 | 940519 | 0.0113864 |
| 23 | 791107 | 0.00957757 |
| 24 | 661672 | 0.00801056 |
| 25 | 554937 | 0.00671837 |
| 26 | 463901 | 0.00561624 |
| 27 | 387339 | 0.00468933 |
| 28 | 324079 | 0.00392347 |
| 29 | 271321 | 0.00328476 |
| 30 | 225978 | 0.00273581 |
| 31 | 189012 | 0.00228828 |
| 32 | 157709 | 0.00190931 |
| 33 | 131845 | 0.00159619 |
| 34 | 109592 | 0.00132678 |
| 35 | 91327 | 0.00110565 |
| 36 | 76216 | 0.00092271 |
| 37 | 63433 | 0.00076795 |
| 38 | 52786 | 0.00063906 |
| 39 | 44122 | 0.00053417 |
| 40 | 36785 | 0.00044534 |
| 41 | 30834 | 0.00037329 |
| 42 | 25494 | 0.00030864 |
| 43 | 21170 | 0.0002563 |
| 44 | 17767 | 0.0002151 |
| 45 | 14657 | 0.00017745 |
| 46 | 12410 | 0.00015024 |
| 47 | 10299 | 0.00012469 |
| 48 | 8666 | 0.00010492 |
| 49 | 7355 | 0.00008904 |
| 50 | 5901 | 0.00007144 |
| 51 | 5017 | 0.00006074 |
| 52 | 4227 | 0.00005117 |
| 53 | 3452 | 0.00004179 |
| 54 | 2888 | 0.00003496 |
| 55 | 2470 | 0.0000299 |
| 56 | 2012 | 0.00002436 |
| 57 | 1626 | 0.00001969 |
| 58 | 1391 | 0.00001684 |
| 59 | 1135 | 0.00001374 |
| 60 | 924 | 0.00001119 |
| 61 | 840 | 0.00001017 |
| 62 | 694 | 0.0000084 |
| 63 | 534 | 0.00000646 |
| 64 | 498 | 0.00000603 |
| 65 | 372 | 0.0000045 |
| 66 | 316 | 0.00000383 |
| 67 | 286 | 0.00000346 |
| 68 | 224 | 0.00000271 |
| 69 | 197 | 0.00000238 |
| 70 | 160 | 0.00000194 |
| 71 | 125 | 0.00000151 |
| 72 | 86 | 0.00000104 |
| 73 | 79 | 0.00000096 |
| 74 | 94 | 0.00000114 |
| 75 | 70 | 0.00000085 |
| 76 | 64 | 0.00000077 |
| 77 | 38 | 0.00000046 |
| 78 | 42 | 0.00000051 |
| 79 | 27 | 0.00000033 |
| 80 | 33 | 0.0000004 |
| 81 | 16 | 0.00000019 |
| 82 | 18 | 0.00000022 |
| 83 | 19 | 0.00000023 |
| 84 | 14 | 0.00000017 |
| 85 | 6 | 0.00000007 |
| 86 | 4 | 0.00000005 |
| 87 | 9 | 0.00000011 |
| 88 | 4 | 0.00000005 |
| 89 | 5 | 0.00000006 |
| 90 | 5 | 0.00000006 |
| 91 | 1 | 0.00000001 |
| 92 | 6 | 0.00000007 |
| 93 | 1 | 0.00000001 |
| 94 | 3 | 0.00000004 |
| 95 | 1 | 0.00000001 |
| 96 | 1 | 0.00000001 |
| 97 | 2 | 0.00000002 |
| 102 | 1 | 0.00000001 |
| Total | 82600000 | 1 |
Consider a hypothetical game based on the roll of a die. If die lands on 1, the player loses $1 and the game ends. If the die lands on anything else, the player’s wins $1. At this point the player may let it ride, or quit. The player may keep playing, doubling each bet, until he loses or quits. What is the best strategy?
Speaking only in terms of maximizing expected value, the player should play forever. While the probability is 1 that the player will eventually lose, at any given decision point the expected value always favors going again. It seems like a paradox. The answer lies in the fact that some events have a probability of 1, but still may not happen. For example, if you threw a dart at a number line from 0 to 10, the probability of not hitting pi exactly is 1, but it still could happen.
However, for practical purposes, there is some stopping point. This is because the happiness money brings is not proportional to the amount. While it is commonly accepted that more money brings more happiness, the richer you get, the less happiness each additional dollar brings you.
I believe a good way to answer this question is to apply the Kelly Criterion to the problem. According to Kelly, the player should make every decision with the goal of maximizing the expected log of his bankroll after the wager. To cut to the end of this (I cut out a lot of math), the player should keep doubling until the wager amount exceeds 96.5948% of his total wealth. Wealth should be defined as the sum of the amount won plus whatever money the player had before he made the first wager. For example, if the player had $100,000 to start with, he should keep doubling up to 23 times, to a win of $4,194,304. At that point the player’s total wealth will be $4,294,304. He will be asked to wager 4,194,304/4,294,304 = 96.67% of his total wealth, which is greater than the 96.5948% stopping point, so he should quit.
Players A and B throw a pair of dice. Player A wins if he throws a total of 6 before B throws a toal of 7, and B wins if he throws 7 before A throws 6. If A begins, show that A’s chances of winning are 30/61.
Let the answer to this question be called p. The probability of rolling a total of six is 5/36, and the probability of rolling a total of seven is 6/36. If you don’t understand why, please see my section on dice probability basics. We can define p as:
p = Prob(6 on first roll) + Prob(no 6 on first roll)*Prob(no 7 on second roll)*p.
This is because, if neither player wins after the first two rolls, the game is back to the original state, and the probability of player A winning remains the same.
So, we have:
p = (5/36) + (31/36)×(30/36)×p
p = 5/36 + (930/1296)×p
p * (1-(930/1296)) = 5/36.
p * (366/1296) = 5/36
p = (5/36)×(1296/366) = 30/61.
How many ways are there to roll n six-sided, non-distinct dice? As stated, the dice are non-distinct, so with five dice, for example, 1-1-3-5-6 and 1-6-5-1-3 would be considered the same roll. With two dice, it’s trivial to determine that the answer is 21, but I can’t figure out an elegant, generalized solution.
The answer can be expressed as combin(n+5,n) = (n+5)!/(120×n!). Here is the answer for 1 to 20 dice.
Non-Distinct Dice Combinations
| Dice | Combinations |
| 1 | 6 |
| 2 | 21 |
| 3 | 56 |
| 4 | 126 |
| 5 | 252 |
| 6 | 462 |
| 7 | 792 |
| 8 | 1287 |
| 9 | 2002 |
| 10 | 3003 |
| 11 | 4368 |
| 12 | 6188 |
| 13 | 8568 |
| 14 | 11628 |
| 15 | 15504 |
| 16 | 20349 |
| 17 | 26334 |
| 18 | 33649 |
| 19 | 42504 |
| 20 | 53130 |
| 21 | 65780 |
| 22 | 80730 |
| 23 | 98280 |
Credit to Alan Tucker, author of Applied Combinatorics.
Can you calculate what the probability is of two numbers coming up behind each other in a roll of the dice? Meaning what is the probability of two 4’s or two 6’s or two 7’s back to back? I realize that the past cannot predict the future but is there a way to calculate 7/36 X 7/36 happening back to back? I hope that makes sence.
Sure. That would be Pr(2)2 + Pr(3)2 + ... + Pr(12)2 = (1/36)2 + (2/36)2 + (3/36)2 + (4/36)2 + (5/36)2 + (6/36)2 + (5/36)2 + (4/36)2 + (3/36)2 + (2/36)2 + (1/36)2 = 11.27%.
In 180 consecutive rolls of the dice, how many times can I expect to see the following:
Two sevens in a row?
Three sevens in a row?
Four sevens in a row?
Thanks for your time :-).
I can’t think of any useful reason to know this information, but I get asked this kind of thing a lot, so I’ll humor you.
It is a little easier getting a specified sequence of sevens starting with the first roll, or ending with the last, because the sequence is bounded on one side. Specifically, the probability of getting a sequence of s sevens, starting with the first roll, or ending with the last, is (1/6)s × (5/6). The 5/6 term is because you have to get a non-7 at the open end of the sequence.
The probability of starting a sequence of s sevens at any point in the middle of the sequence is (1/6)s × (5/6)2. We square the 5/6 term, because the player must get a non-7 on both ends of the sequence.
If there are r rolls, there will be 2 places for an inside sequence, and r-n-1 places for a run of n sevens. Putting these equations in a table, here is the expected number of runs of sevens, from 1 to 10. The "inside" column is 2*(5/6)*(1/6)r, and the "outside" column is (179-r)*(5/6)2*(1/6)r, where r is the number of sevens in the run. So, we can expect 3.46 runs of two sevens, 0.57 runs of three sevens, and 0.10 runs of four sevens.
Expected Runs of Sevens in 180 Rolls
| Run | Inside | Outside | Total |
| 1 | 0.277778 | 20.601852 | 20.87963 |
| 2 | 0.046296 | 3.414352 | 3.460648 |
| 3 | 0.007716 | 0.565844 | 0.57356 |
| 4 | 0.001286 | 0.093771 | 0.095057 |
| 5 | 0.000214 | 0.015539 | 0.015754 |
| 6 | 0.000036 | 0.002575 | 0.002611 |
| 7 | 0.000006 | 0.000427 | 0.000433 |
| 8 | 0.000001 | 0.000071 | 0.000072 |
| 9 | 0 | 0.000012 | 0.000012 |
| 10 | 0 | 0.000002 | 0.000002 |
Two dice are rolled until either a total of 12 or two consecutive totals of 7. What is the probability the 12 is rolled first?
The answer and solution can be found on my companion site, mathproblems.info, problem 201.
I’m a tabletop gamer, and was having some discussion with my friends about non-cubical platonic solid dice (If you’re a big enough nerd, that means d4, d8, d12, and d20). They argued that those would be the only ones that would be demonstratively fair. I argued that manufacturing them to be fair would be entirely too difficult. Also, the only games would be craps variants rendered overly cumbersome due to the number of extra outcomes. Has any casino ever had a game that used non-traditional six sided dice?
|
|
If you limit yourself to the regular polygons, and want every face to have the same probability, then you are limited to the platonic solids. However, if you can lift the regular polygon requirement, then you can add the 13 Catalan solids as well.
To answer your other question, no, I have never seen a game actually in a casino that used any dice other than cubes. About ten years ago I saw a game demonstrated at a gaming show in Atlantic City that I think used a Rhombic triacontahedron, one of the Catalan solids, but I don’t think it ever made it to a casino floor. There is a game I see year after year at the Global Gaming Expo that uses a spinning top (like a dreidel), but alas, I’ve never seen that in a casino either.
If I roll three six-sided dice, what are the odds of rolling a straight and, also, what are the odds of rolling a three of a kind?
There are 63=216 ways to roll three dice. Six of those combinations will result in a three of a kind (1-1-1 to 6-6-6). So the probability of a three of a kind is 6/216 = 1/36. There are four possible spans for a straight (1-2-3 to 4-5-6). There are also 3!=6 ways to arrange the three dice in a straight. So, there are 4*6=24 straight combinations. Thus the probability of a straight is 24/216 = 1/9.
What is the average sum when rolling four six-sided dice after subtracting the lowest result (known as 4d6-L)? What is the standard deviation for this roll?
The following table shows the number of combinations for all possible totals from 3 to 18.
Combinations in 4d6-L
| Outcome | Combinations |
| 3 | 1 |
| 4 | 4 |
| 5 | 10 |
| 6 | 21 |
| 7 | 38 |
| 8 | 62 |
| 9 | 91 |
| 10 | 122 |
| 11 | 148 |
| 12 | 167 |
| 13 | 172 |
| 14 | 160 |
| 15 | 131 |
| 16 | 94 |
| 17 | 54 |
| 18 | 21 |
| Total | 1296 |
The mean result is 12.2446, and the standard deviation is 2.8468.
My question is based on dice odds. I know that there are six ways to get 7 and one way to get 12, but what are the chances of getting six 7’s before one 12? Are they even, and if not, how many twelves should be added to the equation to make it an even proposition?
The probability of rolling a 7 is 1/6, and the probability of rolling a 12 is 1/36. The probability of rolling a 7, given that a roll is a 7 or 12 is (1/6)/((1/6)+(1/36)) = 6/7. So the probability that the first six times a 6 or 12 is rolled it is a 6 every time is (6/7)6 = 39.66%.
If you rephrase the question to be what is the probability of rolling five 6’s before a 12, then the answer is (6/7)5 = 46.27%. With four rolls it is (6/7)4 = 53.98%. So there is no number of 7’s before a 12 that is exactly 50/50. If you’re looking for a good sucker bet, suggest you can either roll four 7’s before a 12, or a 12 before five 7’s.
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
Is there an easy way to calculate the probability of throwing a total of t with d 6-sided dice?
Here is a handy trick, courtesy of Robert Goodhand of Somerset, UK. First put on a row six ones surrounded by five zeros on either side, as follows:
One-Die Probabilities
| Dice Total | 1 | 2 | 3 | 4 | 5 | 6 | ||||||||||
| One Die | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
This represents the number of combinations for rolling a 1 to 6 with one die. I know, pretty obvious. However, stick with me. For two dice, add another row to the bottom, and for each cell take the sum of the row above and the five cells to the left of it. Then add another five dummy zeros to the right, if you wish to keep going. This represents the combinations of rolling a total of 2 to 12.
Two Dice Probabilities
| Dice Total | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||||||||||
| One Die | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Two Dice | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | 0 | 0 | 0 | 0 |
For three dice, just repeat. This will represent the number of combinations of 3 to 18.
To get the probability of any given total, divide the number of combinations of that total by the total number of combinations. In the case of three dice, the sum is 216, which also easily found as 63. For example, the probability of rolling a total of 13 with three dice is 21/216 = 9.72%.
So for d dice, you’ll need to work your way up through 1 to d-1 dice. This is very easily accomplished in any spreadsheet.
How many rolls of two dice would it take to have a 50/50 chance of rolling at least one 12?
That is a classic problem in the history of the field of probability. Many people incorrectly think the answer is 18, because the probability of a 12 is 1 in 36, and 18×(1/36)=50%. However, by that logic, the probability of getting a 12 in 36 rolls would be 100%, which clearly it isn’t. Here is the correct solution. Let r be the number of rolls. The probability a roll isn’t a 12 is 35/36. The probability there are 0 12s in r rolls is (35/36)r. So we need to solve for r in the following equation:
(35/36)r = 0.5
log(35/36)r = log(0.5)
r × log(35/36) = log(0.5)
r = log(0.5)/log(35/36)
r = 24.6051
So there isn’t a round answer. The probability of rolling a 12 in 24 rolls is 1-(35/36)24 = 49.14%. The probability of rolling a 12 in 25 rolls is 1-(35/36)25 = 50.55%.
If you want to make a bet on this, say you can roll a 12 in 25 rolls, or somebody else can’t in 24 rolls. Either way you’ll have an advantage at even money.
In Dice Wars, what is the probability of success for any given number of attacking and defending dice? As an attacker, what ratio has the greatest expected gain?
For those unfamiliar with the game, both the attacker and defender will roll 1 to 8 dice, according to how many armies they each have at that point in a battle. The higher total shall win. A tie goes to the defender. If the attacker loses, he will still retain one army in the territory where he initiated the attack. For this reason, he must have at least two armies to attack, so if he wins one can inhabit the conquered territory and one can stay behind.
The following table shows the probability of an attacker victory according to all 64 combinations of total dice.
Probability of Attacker Win
| Attacker | Defender | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 Army | 2 Armies | 3 Armies | 4 Armies | 5 Armies | 6 Armies | 7 Armies | 8 Armies | |
| 2 | 0.837963 | 0.443673 | 0.152006 | 0.035880 | 0.006105 | 0.000766 | 0.000071 | 0.000005 |
| 3 | 0.972994 | 0.778549 | 0.453575 | 0.191701 | 0.060713 | 0.014879 | 0.002890 | 0.000452 |
| 4 | 0.997299 | 0.939236 | 0.742831 | 0.459528 | 0.220442 | 0.083423 | 0.025450 | 0.006379 |
| 5 | 0.999850 | 0.987940 | 0.909347 | 0.718078 | 0.463654 | 0.242449 | 0.103626 | 0.036742 |
| 6 | 0.999996 | 0.998217 | 0.975300 | 0.883953 | 0.699616 | 0.466731 | 0.259984 | 0.121507 |
| 7 | 1.000000 | 0.999801 | 0.994663 | 0.961536 | 0.862377 | 0.685165 | 0.469139 | 0.274376 |
| 8 | 1.000000 | 0.999983 | 0.999069 | 0.989534 | 0.947731 | 0.843874 | 0.673456 | 0.471091 |
The next table shows the expected gain by the attacker, defined as pr(attacker wins)*(defender dice)+pr(defender wins)*(attacker dice -1). It shows the greatest expected gain is to attack with 8 against an opponent with 5.
Net Gain of Attacker Win
| Attacker | Defender | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 Army | 2 Armies | 3 Armies | 4 Armies | 5 Armies | 6 Armies | 7 Armies | 8 Armies | |
| 2 | 0.675926 | 0.331019 | -0.391976 | -0.820600 | -0.963370 | -0.994638 | -0.999432 | -0.999955 |
| 3 | 0.918982 | 1.114196 | 0.267875 | -0.849794 | -1.575009 | -1.880968 | -1.973990 | -1.995480 |
| 4 | 0.989196 | 1.696180 | 1.456986 | 0.216696 | -1.236464 | -2.249193 | -2.745500 | -2.929831 |
| 5 | 0.999250 | 1.927640 | 2.365429 | 1.744624 | 0.172886 | -1.575510 | -2.860114 | -3.559096 |
| 6 | 0.999976 | 1.987519 | 2.802400 | 2.955577 | 1.996160 | 0.134041 | -1.880192 | -3.420409 |
| 7 | 1.000000 | 1.998408 | 2.951967 | 3.615360 | 3.486147 | 2.221980 | 0.098807 | -2.158736 |
| 8 | 1.000000 | 1.999847 | 2.990690 | 3.884874 | 4.372772 | 3.970362 | 2.428384 | 0.066365 |
What is the probability of forming a Yahtzee with up to n rolls of the dice?
For the benefit of other readers, a Yahtzee is a five of a kind with five dice. In the game of Yahtzee the player may hold any dice he wishes and re-roll the rest. He can do this up to three rolls.
The player may re-roll previously held dice, if he wishes. For example, if the player's first roll is 3-3-4-5-6 and he holds the threes and then has 3-3-5-5-5 after the second roll he may keep the fives and re-roll the threes on his third roll.
The following table shows the maximum number of dice of the same face for 1 to 20 rolls. The table shows the probability of getting a Yahtzee within three rolls is about 4.6%.
Yahtzee Probabilities
| Rolls | Maximum Dice of Same Face | ||||
|---|---|---|---|---|---|
| One | Two | Three | Four | Five | |
| 1 | 0.092593 | 0.694444 | 0.192901 | 0.019290 | 0.000772 |
| 2 | 0.008573 | 0.450103 | 0.409022 | 0.119670 | 0.012631 |
| 3 | 0.000794 | 0.256011 | 0.452402 | 0.244765 | 0.046029 |
| 4 | 0.000074 | 0.142780 | 0.409140 | 0.347432 | 0.100575 |
| 5 | 0.000007 | 0.079373 | 0.337020 | 0.413093 | 0.170507 |
| 6 | 0.000001 | 0.044101 | 0.263441 | 0.443373 | 0.249085 |
| 7 | 0.000000 | 0.024501 | 0.199279 | 0.445718 | 0.330502 |
| 8 | 0.000000 | 0.013612 | 0.147462 | 0.428488 | 0.410438 |
| 9 | 0.000000 | 0.007562 | 0.107446 | 0.398981 | 0.486011 |
| 10 | 0.000000 | 0.004201 | 0.077416 | 0.362855 | 0.555528 |
| 11 | 0.000000 | 0.002334 | 0.055317 | 0.324175 | 0.618174 |
| 12 | 0.000000 | 0.001297 | 0.039279 | 0.285674 | 0.673750 |
| 13 | 0.000000 | 0.000720 | 0.027757 | 0.249063 | 0.722460 |
| 14 | 0.000000 | 0.000400 | 0.019543 | 0.215313 | 0.764744 |
| 15 | 0.000000 | 0.000222 | 0.013720 | 0.184883 | 0.801175 |
| 16 | 0.000000 | 0.000124 | 0.009610 | 0.157896 | 0.832371 |
| 17 | 0.000000 | 0.000069 | 0.006719 | 0.134258 | 0.858954 |
| 18 | 0.000000 | 0.000038 | 0.004692 | 0.113753 | 0.881517 |
| 19 | 0.000000 | 0.000021 | 0.003272 | 0.096100 | 0.900607 |
| 20 | 0.000000 | 0.000012 | 0.002280 | 0.080994 | 0.916714 |
This question is raised and discussed in my forum at Wizard of Vegas.
I am wondering which will come up more rolling a pair of dice — an odd or even total?
The answer is 50/50. This will be true for any number of dice rolled, not just two.
A bit off-topic, but I've always thought an odd/even set of bets would be a good way to replace the dreaded big 6/8 bets in craps. To give the house an advantage, here are my proposed pay tables and analysis.
Odd Bet
| Event | Pays | Combinations | Probability | Return |
|---|---|---|---|---|
| 3 or 11 | 1.5 | 4 | 0.111111 | 0.166667 |
| 5 or 9 | 1 | 8 | 0.222222 | 0.222222 |
| 7 | 0.5 | 6 | 0.166667 | 0.083333 |
| Even | -1 | 18 | 0.500000 | -0.500000 |
| Total | 36 | 1.000000 | -0.027778 |
Even Bet
| Event | Pays | Combinations | Probability | Return |
|---|---|---|---|---|
| 2 or 12 | 3 | 2 | 0.055556 | 0.166667 |
| 4 or 10 | 1 | 6 | 0.166667 | 0.166667 |
| 6 or 8 | 0.5 | 10 | 0.277778 | 0.138889 |
| Odd | -1 | 18 | 0.500000 | -0.500000 |
| Total | 36 | 1.000000 | -0.027778 |
Please note that I claim all rights with this publication.
This question is raised and discussed in my forum at Wizard of Vegas.
In the Hot Roll bonus, the player wins the following number of coins according to the total of two dice:
- 2 or 12: 1000
- 3 or 11: 600
- 4 or 10: 400
- 5 or 9: 300
- 6 or 8: 200
He keeps rolling until he gets a total of seven, which ends the bonus. If he rolls a seven on the first roll, then he gets a consolation prize of 700 coins. What is the average coins won per bonus?
The average number of rolls is the inverse of the bonus-ending event, which has a probability of 1/6, so the player will roll six times on average. However, the last roll will be the seven, so an average of five winning rolls per bonus.
Next, here is the probability of each total, assuming no seven:
- 2 or 12: 1/30
- 3 or 11: 2/30
- 4 or 10: 3/30
- 5 or 9: 4/30
- 6 or 8: 5/30
So, the average win per roll, assuming no seven, is 2*[(1/30)*1000 + (2/30)*600 + (3/30)*400 + (4/30)*300 + (5/30)*200] = 373.33.
The value of the consolation prize is (1/6)*700 = 116.67.
Thus, the average bonus win is 116.67 + 5×373.33 = 1983.33.
What would be the answer to the dice problem in Ask the Wizard column #179, if the players took turns rolling the dice and only the player rolling could advance based on the roll?
Here was the original question posted in column #179: If two dice are rolled over and over, until either of the following events happen, then which is more likely to happen first:
- A total of six and eight is rolled, in either order, with duplicates allowed.
- A total of seven is rolled twice.
Your twist is that the same roll can't help both players. Instead, they take turns rolling and only the one rolling can use the roll.
The answer depends on who rolls first. If the player needing a six and eight rolls first, then he has a probability of winning of 57.487294%. If the player needing two sevens goes first, then the probability the player needing the six and eight wins is 52.671614%. I solved it using a simple Markov Chain process.
This question is asked and discussed in my forum at Wizard of Vegas.
Suppose you have 12 six-sided dice. You roll them and may set aside any dice you wish. You then re-roll the other dice. What is the probability of getting a 12-of-a-kind in the two rolls?
There are 58 different types of sequences on the initial roll. The way I identify each is the number of the face in majority, then the number of dice of the face second in total, and so on. For example, a roll of of 3,3,3,3,6,6,6,5,5,2 would be signified as 4-3-2-1. The following table shows the number of combinations of each sequence, the probability of rolling it, the probability of completing a 12 of a kind in the second roll, and the product of the two. For the probability on the second roll, I assume the player holds the dice that have the greatest total on the initial roll. The lower right cell shows an overall probability of 0.0000037953, which equals 1 in 263,486.
12 Dice Question
| Sequence | Combinations | Probability Sequence |
Conditional Probability |
Total Probability |
|---|---|---|---|---|
| 12-0-0-0-0-0 | 6 | 0.0000000028 | 1.0000000000 | 0.0000000028 |
| 11-1-0-0-0-0 | 360 | 0.0000001654 | 0.1666666667 | 0.0000000276 |
| 10-2-0-0-0-0 | 1,980 | 0.0000009096 | 0.0277777778 | 0.0000000253 |
| 10-1-1-0-0-0 | 7,920 | 0.0000036384 | 0.0277777778 | 0.0000001011 |
| 9-3-0-0-0-0 | 6,600 | 0.0000030320 | 0.0046296296 | 0.0000000140 |
| 9-2-1-0-0-0 | 79,200 | 0.0000363840 | 0.0046296296 | 0.0000001684 |
| 9-1-1-1-0-0 | 79,200 | 0.0000363840 | 0.0046296296 | 0.0000001684 |
| 8-4-0-0-0-0 | 14,850 | 0.0000068220 | 0.0007716049 | 0.0000000053 |
| 8-3-1-0-0-0 | 237,600 | 0.0001091519 | 0.0007716049 | 0.0000000842 |
| 8-2-2-0-0-0 | 178,200 | 0.0000818639 | 0.0007716049 | 0.0000000632 |
| 8-2-1-1-0-0 | 1,069,200 | 0.0004911837 | 0.0007716049 | 0.0000003790 |
| 8-1-1-1-1-0 | 356,400 | 0.0001637279 | 0.0007716049 | 0.0000001263 |
| 7-5-0-0-0-0 | 23,760 | 0.0000109152 | 0.0001286008 | 0.0000000014 |
| 7-4-1-0-0-0 | 475,200 | 0.0002183039 | 0.0001286008 | 0.0000000281 |
| 7-3-2-0-0-0 | 950,400 | 0.0004366077 | 0.0001286008 | 0.0000000561 |
| 7-3-1-1-0-0 | 2,851,200 | 0.0013098232 | 0.0001286008 | 0.0000001684 |
| 7-2-2-1-0-0 | 4,276,800 | 0.0019647348 | 0.0001286008 | 0.0000002527 |
| 7-2-1-1-1-0 | 5,702,400 | 0.0026196464 | 0.0001286008 | 0.0000003369 |
| 7-1-1-1-1-1 | 570,240 | 0.0002619646 | 0.0001286008 | 0.0000000337 |
| 6-6-0-0-0-0 | 13,860 | 0.0000063672 | 0.0000214335 | 0.0000000001 |
| 6-5-1-0-0-0 | 665,280 | 0.0003056254 | 0.0000214335 | 0.0000000066 |
| 6-4-2-0-0-0 | 1,663,200 | 0.0007640635 | 0.0000214335 | 0.0000000164 |
| 6-4-1-1-0-0 | 4,989,600 | 0.0022921906 | 0.0000214335 | 0.0000000491 |
| 6-3-3-0-0-0 | 1,108,800 | 0.0005093757 | 0.0000214335 | 0.0000000109 |
| 6-3-2-1-0-0 | 19,958,400 | 0.0091687624 | 0.0000214335 | 0.0000001965 |
| 6-3-1-1-1-0 | 13,305,600 | 0.0061125083 | 0.0000214335 | 0.0000001310 |
| 6-2-2-2-0-0 | 4,989,600 | 0.0022921906 | 0.0000214335 | 0.0000000491 |
| 6-2-2-1-1-0 | 29,937,600 | 0.0137531436 | 0.0000214335 | 0.0000002948 |
| 6-2-1-1-1-1 | 9,979,200 | 0.0045843812 | 0.0000214335 | 0.0000000983 |
| 5-5-2-0-0-0 | 997,920 | 0.0004584381 | 0.0000035722 | 0.0000000016 |
| 5-5-1-1-0-0 | 2,993,760 | 0.0013753144 | 0.0000035722 | 0.0000000049 |
| 5-4-3-0-0-0 | 3,326,400 | 0.0015281271 | 0.0000035722 | 0.0000000055 |
| 5-4-2-1-0-0 | 29,937,600 | 0.0137531436 | 0.0000035722 | 0.0000000491 |
| 5-4-1-1-1-0 | 19,958,400 | 0.0091687624 | 0.0000035722 | 0.0000000328 |
| 5-3-3-1-0-0 | 19,958,400 | 0.0091687624 | 0.0000035722 | 0.0000000328 |
| 5-3-2-2-0-0 | 29,937,600 | 0.0137531436 | 0.0000035722 | 0.0000000491 |
| 5-3-2-1-1-0 | 119,750,400 | 0.0550125743 | 0.0000035722 | 0.0000001965 |
| 5-3-1-1-1-1 | 19,958,400 | 0.0091687624 | 0.0000035722 | 0.0000000328 |
| 5-2-2-2-1- | 59,875,200 | 0.0275062872 | 0.0000035722 | 0.0000000983 |
| 5-2-2-1-1-1 | 59,875,200 | 0.0275062872 | 0.0000035722 | 0.0000000983 |
| 4-4-4-0-0-0 | 693,000 | 0.0003183598 | 0.0000005954 | 0.0000000002 |
| 4-4-3-1-0-0 | 24,948,000 | 0.0114609530 | 0.0000005954 | 0.0000000068 |
| 4-4-2-2-0-0 | 18,711,000 | 0.0085957147 | 0.0000005954 | 0.0000000051 |
| 4-4-2-1-1-0 | 74,844,000 | 0.0343828589 | 0.0000005954 | 0.0000000205 |
| 4-4-1-1-1-1 | 12,474,000 | 0.0057304765 | 0.0000005954 | 0.0000000034 |
| 4-3-3-2-0-0 | 49,896,000 | 0.0229219060 | 0.0000005954 | 0.0000000136 |
| 4-3-3-1-1-0 | 99,792,000 | 0.0458438119 | 0.0000005954 | 0.0000000273 |
| 4-3-2-2-1-0 | 299,376,000 | 0.1375314358 | 0.0000005954 | 0.0000000819 |
| 4-3-2-1-1-1 | 199,584,000 | 0.0916876238 | 0.0000005954 | 0.0000000546 |
| 4-2-2-2-2-0 | 37,422,000 | 0.0171914295 | 0.0000005954 | 0.0000000102 |
| 4-2-2-2-1-1 | 149,688,000 | 0.0687657179 | 0.0000005954 | 0.0000000409 |
| 3-3-3-3-0-0 | 5,544,000 | 0.0025468784 | 0.0000000992 | 0.0000000003 |
| 3-3-3-2-1-0 | 133,056,000 | 0.0611250826 | 0.0000000992 | 0.0000000061 |
| 3-3-3-1-1-1 | 44,352,000 | 0.0203750275 | 0.0000000992 | 0.0000000020 |
| 3-3-2-2-2-0 | 99,792,000 | 0.0458438119 | 0.0000000992 | 0.0000000045 |
| 3-3-2-2-1-1 | 299,376,000 | 0.1375314358 | 0.0000000992 | 0.0000000136 |
| 3-2-2-2-2-1 | 149,688,000 | 0.0687657179 | 0.0000000992 | 0.0000000068 |
| 2-2-2-2-2-2 | 7,484,400 | 0.0034382859 | 0.0000000165 | 0.0000000001 |
| Total | 2,176,782,336 | 1.0000000000 | 0.0000037953 |
On average, how many rolls of a fair die are needed to roll every face at least twice?
Click the button below for the answer.
Here is my solution. (PDF)
This question is asked and discussed in my forum at Wizard of Vegas.
Suppose a fair six-sided die is rolled until a 1, 2, 3, or 6 appears. If a 1, 2, or 3 is the first of these game-ending numbers to appear, then you win nothing. If a 6 is the first of these game-ending numbers to appear, then you win $1 for every roll of the die. What is the average win of this game?
Click the button below for a couple infinite series formulas that you may find helpful.
Hint 1: Sum for i = 0 to ∞ of ni = 1 / (1-n)
Hint 2: Sum for i = 0 to ∞ of i × ni = n / (1-n)2
Click the button below for the answer.
Click the button below for the solution.
Suppose a fair six-sided die is rolled until a 1, 2, 3, or 6 appears. If a 1, 2, or 3 is the first of these game-ending numbers to appear, then you win nothing. If a 6 is the first of these game-ending numbers to appear, then you win $1 for every roll of the die. What is the average win of this game?
Hint 1: Sum for i = 0 to ∞ of ni = 1 / (1-n)
Hint 2: Sum for i = 0 to ∞ of i × ni = n / (1-n)2
The expected win can be expressed as the sum for i = 0 to ∞ of (1 + i) * (1/3)i * (1/6). =
(1/6) * sum for i = 0 to ∞ of (1/3)i + (1/6) * sum for i = 0 to ∞ of (i * (1/3)i).
Let's evaluate these one at a time.
sum for i = 0 to ∞ of (1/3)i =
1 / (1 - (1/3)) =
1 / (2/3) =
3/2
Sum for i = 0 to ∞ of (i * (1/3)i) =
(1/3) / (1 - (1/3))2 =
(1/3) / (4/9) =
(1/3) * (9/4) =
3/4
Putting it all together, the answer is
(1/6) * (3/2) + (1/6)*(3/4) =
(1/4) + (1/8) =
3/8
This question is asked and discussed in my forum at Wizard of Vegas.
What is the expected number of rolls of a fair die to roll every face at least twice?
While this could be solved with a long and tedious Markov chain, I prefer an integral solution. I explain how to use this method in my pages on the Fire Bet and Bonus Craps.
Imagine that instead of significant events being determined by the roll of the die, one at a time, consider them as an instant in time. Assume the time between events has a memory-less property, with an average time between events of one unit of time. In other words, the time between events follows an exponential distribution with a mean of 1. This will not matter for purposes of adjudicating the bet, because events still happen one at a time.
Per the Poisson distribution, the probability that any given side of the die has been rolled zero times in x units of time is exp(-x/6)*(x/6)0/0! = exp(-x/6). Poisson also say the probability of any given side being rolled exactly once is exp(-x/6)*(x/6)1/1! = exp(-x/6) * (x/6). Thus probability any side has been rolled two or more times in x units of time is 1 - exp(-x/6)*(1 + (x/6)). The probability that all six sides have been rolled at least twice is (1 - exp(-x/6)*(1 + (x/6)))6. The probability that at least one side has not been rolled at least twice is equal to:
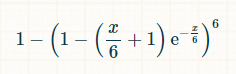
We need to integrate that over all time to find how much time will go by, on average, where the desired goal has not been achieved.
Fortunately, we can use an integral calculator at this point. For the one linked to, put 1- (1 - exp(-x/6)*(1 + x/6))^6 dx = apx. 24.1338692 in the text box following "Calculate the integral of" and under custom, set the bound of integration from 0 to ∞.
The answer is 390968681 / 16200000 = apx. 24.13386919753086
This question is asked and discussed in my forum at Wizard of Vegas.
You start with a fair 6-sided die and roll it six times, recording the results of each roll. You then write these numbers on the six faces of another, unlabeled fair die. For example, if your six rolls were 3, 5, 3, 6, 1 and 2, then your second die wouldn’t have a 4 on it; instead, it would have two 3s.
Next, you roll this second die six times. You take those six numbers and write them on the faces of yet another fair die, and you continue this process of generating a new die from the previous one.
Eventually, you’ll have a die with the same number on all six faces. What is the average number of transitions from one die to another (or total rolls divided by 6) to reach this state?
Let's label the initial die with letters instead of numbers, to avoid confusion. Let's label each possible die state with letters. For example, AAABBC would mean three of one letter, two of another, and one of a third. The initial state would obviously be ABCDEF.
Let E(ABCDEF) be the expected number of rolls from state ABCDEF.
E(ABCDEF) = 1 + [180 × E(AAAAAB) + 450 × E(AAAABB) + 300 × E(AAABBB) + 1800 × E(AAAABC) + 7200 × E(AAABBC) + 1800 × E(AABBCC) + 7200 × E(AAABCD) + 16200 × E(AABBCD) + 10800 × E(AABCDE) + 720 × E(ABCDEF)]/46656Building on the number of combinations of going from one state to another, the following transition matrix shows how many ways there are for going from each initial state (left column) to each new state. This took a few hours to construct properly, by the way.
Transition Matrix A
| State Before |
AAAAAA | AAAAAB | AAAABB | AAABBB | AAAABC | AAABBC | AABBCC | AAABCD | AABBCD | AABCDE | ABCDEF |
|---|---|---|---|---|---|---|---|---|---|---|---|
| AAAAAB | 15,626 | 18,780 | 9,750 | 2,500 | - | - | - | - | - | - | - |
| AAAABB | 4,160 | 13,056 | 19,200 | 10,240 | - | - | - | - | - | - | - |
| AAABBB | 1,458 | 8,748 | 21,870 | 14,580 | - | - | - | - | - | - | - |
| AAAABC | 4,098 | 12,348 | 8,190 | 2,580 | 7,920 | 10,080 | 1,440 | - | - | - | - |
| AAABBC | 794 | 5,172 | 8,670 | 5,020 | 6,480 | 17,280 | 3,240 | - | - | - | - |
| AABBCC | 192 | 2,304 | 5,760 | 3,840 | 5,760 | 23,040 | 5,760 | - | - | - | - |
| AAABCD | 732 | 4,464 | 4,140 | 1,680 | 7,920 | 14,400 | 2,520 | 4,320 | 6,480 | - | - |
| AABBCD | 130 | 1,596 | 3,150 | 1,940 | 5,280 | 16,800 | 3,600 | 4,800 | 9,360 | - | - |
| AABCDE | 68 | 888 | 1,380 | 760 | 3,960 | 11,520 | 2,520 | 7,200 | 14,040 | 4,320 | - |
| ABCDEF | 6 | 180 | 450 | 300 | 1,800 | 7,200 | 1,800 | 7,200 | 16,200 | 10,800 | 720 |
I won't go into a long lecture on matrix algebra, except to say let's say matrix B is as follows:
Matrix B
| State Before |
AAAAAB | AAAABB | AAABBB | AAAABC | AAABBC | AABBCC | AAABCD | AABBCD | AABCDE | ABCDEF |
|---|---|---|---|---|---|---|---|---|---|---|
| AAAAAB | -27876 | 9750 | 2500 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| AAAABB | 13056 | -27456 | 10240 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| AAABBB | 8748 | 21870 | -32076 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| AAAABC | 12348 | 8190 | 2580 | -38736 | 10080 | 1440 | 0 | 0 | 0 | -46656 |
| AAABBC | 5172 | 8670 | 5020 | 6480 | -29376 | 3240 | 0 | 0 | 0 | -46656 |
| AABBCC | 2304 | 5760 | 3840 | 5760 | 23040 | -40896 | 0 | 0 | 0 | -46656 |
| AAABCD | 4464 | 4140 | 1680 | 7920 | 14400 | 2520 | -42336 | 6480 | 0 | -46656 |
| AABBCD | 1596 | 3150 | 1940 | 5280 | 16800 | 3600 | 4800 | -37296 | 0 | -46656 |
| AABCDE | 888 | 1380 | 760 | 3960 | 11520 | 2520 | 7200 | 14040 | -42336 | -46656 |
| ABCDEF | 180 | 450 | 300 | 1800 | 7200 | 1800 | 7200 | 16200 | 10800 | -46656 |
The answer is the determinant of matrix B to that of matrix A:
Determ(A) = 1,461,067,501,120,670,000,000,000,000,000,000,000,000,000,000
Determ(B) = 14,108,055,348,203,100,000,000,000,000,000,000,000,000,000,000
Determ(B) / Determ(A) = apx. 9.65599148388557
If you roll a single die 20 times, what is the probability you hit all six sides at least once?
The answer could be approximated as expressed 1 - (prob(no 1's) + prob(no 2's) + ... + prob(no 6's)) = 1 - 6*(5/6)^20 = apx. 0.84349568.
However that would double-subtract the situations where two different sides never got rolled. There are combin(6,2)=15 ways to choose two sides out of six. The probability that any two given sides never get rolled is (4/6)^20. We need to add those to the probability, because they got subtracted twice in the previous step. So, now we're at 1 - 6*(5/6)^20 + 15*(4/6)^20 = apx. 0.84800661.
This question is asked and discussed in my forum at Wizard of Vegas.
However, if any group of three sides that had never been rolled would have been triple-subtracted in the first step and triple-added in the second step. We need to subtract them back out as a state where not all six sides were rolled. There are combin(6,3) = 20 ways to choose three sides out of six. The probability that any specific three sides are never rolled is (3/6)^20. So, now we're at 1 - 6*(5/6)^20 + 15*(4/6)^20 - 20*(3/6)^20= apx. 0.847987537.
However, if any group of four sides that had never been rolled would have been quadruple-subtracted in the first step, quadruple-added in the second step, and quadruple subtracted in the third step. We need to add them back in, because each such state was already subtracted out twice. There are combin(6,4) = 15 ways to choose four sides out of six. The probability that any specific four sides are never rolled is (2/6)^20. So, now we're at 1 - 6*(5/6)^20 + 15*(4/6)^20 - 20*(3/6)^20 + 15*(2/6)^20 = apx. 0.84798754089.
However, if all 20 rolls were the same numbers, this situation would have been quintuple-subtracted in the first step, quintuple-added in the first step, quintuple-subtracted in the third step, and quintuple-added in the fourth step. We need to subtracted them back out. So, now we're at 1 - 6*(5/6)^20 + 15*(4/6)^20 - 20*(3/6)^20 + 15*(2/6)^20 - 6*(1/6)^20 = apx. 0.84798754089.
So the answer is 1-6*(5/6)^20+COMBIN(6,4)*(4/6)^20-COMBIN(6,3)*(3/6)^20+COMBIN(6,2)*(2/6)^20-6*(1/6)^20 = apx. 0.84798754089.
You have two cubes. You can number each side of both dice as you wish, as long as each side is an integer and greater or equal to one. You may repeat the same number on the same die and go as high as you wish. Other than creating standard dice, how can you number them so the probability of any given total is the same as standard dice?
Die 1 = 1,2,2,3,3,4.
Die 2 = 1,3,4,5,6,8.
I'm afraid my solution to this one was pretty much trial and error.
What is the average number of rolls needed with two dice to achieve every total from 2 to 12?
One could use a Markov chain to answer this, but I prefer calculus. The key is that the answer is the same if the time between rolls is the exponentially distributed with a mean of one. That said, the answer can be expressed as the integral from 0 to infinity of:
1-(1-exp(-x/36))^2*(1-exp(-x/18))^2*(1-exp(-x/12))^2*(1-exp(-x/9))^2*(1-exp(-5*x/36))^2*(1-exp(-x/6))
You may easily solve such integrals with an integral calculator.
You may also solve any such problem with my Expected Trials Calculator.
Drop Dead is a game played with five standard dice. You begin your turn by rolling all five dice. If none of them are a 2 or 5, you total the dice, add the sum to your point score and roll again. If you do roll any 2s or 5s, your score for the roll is zero. All the dice showing a 2 or 5 are declared dead and set aside. You then roll again with the remaining dice. Play continues with you either scoring points or removing dice. Your turn ends when all your dice are eliminated whereupon you are said to have dropped dead. All your scoring rolls are added together for your final score. High score wins.
What is your expected score for this game?
Let's start with the scenario with one die left and move backwards.
Let the variable a be the expected additional points with one die left.
The average roll that isn't a 2 or 5 is (1+3+4+6)/4 = 7/2.
a = (2/3)×(a + 7/2).
a/3 = 7/3.
a = 7.
Next, let's calculate b, the expected points with two dice left.
b = (2/3)2×(b + 2 × (7/2)) + 2×(2/3)×(1/3)×a.
b = 11.2.
Next, let's calculate c, the expected points with three dice left.
c = (2/3)3×(c + 3× (7/2)) + 3×(2/3)2×(1/3)×b + 3×(2/3)×(1/3)2×b.
c = 1302/95 = 13.705263.
Next, let's calculate d, the expected points with four dice left.
d = (2/3)4×(d + 4× (7/2)) + 4×(2/3)3×(1/3)×c + 6×(2/3)2×(1/3)2×b + 4×(2/3)×(1/3)3×a.
d = 3752/247 = 15.190283.
Finally, let's calculate e, the expected points with five dice left.
e = (2/3)5×(e + 5×(7/2)) + 5×(2/3)4×(1/3)×d + 10×(2/3)3×(1/3)2×c + 10×(2/3)2×(1/3)3×b + 5×(2/3)×(1/3)4×a.
e = 16.064662.
This question is asked and discussed in my forum at Wizard of Vegas.
Roll two dice, a red die and a blue die, over and over. Keep track of the sum of rolls for each die. What is the expected number of roles until these two cumulative totals are equal?
It is hard to explain why the answer is infinity. To make matters more confusing and paradoxical, the probability the totals ever being equal is 1.
The following table shows the probability the totals will be the same for the first time after 1 to 16 rolls.
Probability Equal Totals for First Time
| Rolls | Probability |
|---|---|
| 1 | 0.166667 |
| 2 | 0.112654 |
| 3 | 0.092850 |
| 4 | 0.080944 |
| 5 | 0.072693 |
| 6 | 0.066539 |
| 7 | 0.061722 |
| 8 | 0.057819 |
| 9 | 0.054573 |
| 10 | 0.051819 |
| 11 | 0.049443 |
| 12 | 0.047367 |
| 13 | 0.045532 |
| 14 | 0.043895 |
| 15 | 0.042423 |
| 16 | 0.041089 |
Excel shows a very close fit to this curve is y = 0.1784*x-1.011, where x = number of rolls and y = probability.
The sum of this infinite series is infinity.
This question is asked and discussed in my forum at Wizard of Vegas.
Five red dice and five blue dice are rolled. What is the probability the roll is the same for both dice, without regard to order. For example, both rolls are 1-2-3-3-6.
The following the table shows for any type of roll:
- The number of different ways this roll can be achieved. For example, for a full house, there are six combinations for the three of a kind and five left for the pair, for a total of 30 different full houses.
- The number of orders. For example, for a full house, there are combin(5,3)=10 ways to choose three out of five dice for the three of a kind. The other two must have the pair.
- The number of ways the given hand can be rolled. This is the product for the first two columns. For example, there are 30 * 10 = 300 ways to roll a full house.
- The probability of the hand. For example, for a full house the probability is 300/65 = 0.038580.
- The probability both rolls are the same and of the given hand. This is the probability from column four squared divided by the second column. For example, the probability two rolls are both a full house is 0.0385802. However, the probability they are the same house is 1/30. So, the probability both rolls are the same full house is 0.0385802/30 = 0.00004961.
The lower right cell shows the total probability both rolls are the same is 0.00635324.
Matching Roll
| Type of Roll |
Different Types |
Orders | Total Combinations |
Probability One Roll |
Probability Two Rolls |
|
|---|---|---|---|---|---|---|
| Five of a kind | 6 | 1 | 6 | 0.00077160 | 0.00000010 | |
| Four of a kind | 30 | 5 | 150 | 0.01929012 | 0.00001240 | |
| Full house | 30 | 10 | 300 | 0.03858025 | 0.00004961 | |
| Three of a kind | 60 | 20 | 1,200 | 0.15432099 | 0.00039692 | |
| Two pair | 60 | 30 | 1,800 | 0.23148148 | 0.00089306 | |
| Pair | 60 | 60 | 3,600 | 0.46296296 | 0.00357225 | |
| Five singletons | 6 | 120 | 720 | 0.09259259 | 0.00142890 | |
| Total | 7,776 | 1.00000000 | 0.00635324 |
A six-sided die is rolled until either of the following events happen:
A) Any side has appeared six times.
B) Every side has appeared at least once.
What is the probability event A occurs first?
To answer this one as I did, using calculus, I recommend an integral calculator like the one at integral-calculator.com/.
Here is my solution (PDF).
This problem is asked (in slightly different words) and discussed in my forum at Wizard of Vegas.
You wish to play a game that requires an ordinary six-sided die. Unfortunately, you lost the die. However, you have four index cards, which you may mark any way you like. The player must choose two cards randomly from the four, without replacement, and take the sum of the two cards.
How can you number the cards so that the sum of two different cards represents the roll of a die?
Number them 0, 1, 2, and 4.
There are six ways to draw two out of four cards, as follows.
- 0+1 = 1
- 0+2 = 2
- 1+2 = 3
- 0+4 = 4
- 1+4 = 5
- 2+4 = 6
This question is asked and discussed in my forum at Wizard of Vegas.
A six-sided die is rolled over and over until the sum of rolls is 13 or greater. What is the mean, median and mode of the final total?
Median = 14
Mode = 13
I had to use a Markov Chain for this one. The following table shows the probability of each final total according to the running sum in the left column. Start with the obvious cases for totals of 13 to 18. Then, for running sums of 0 to 12, take the average of the six cells below.
The probabilities for the initial state can be found in the first row for a sum of 0.
Markov Chain
| Sum of Rolls | 13 | 14 | 15 | 16 | 17 | 18 |
|---|---|---|---|---|---|---|
| 0 | 0.279263 | 0.236996 | 0.192313 | 0.145585 | 0.097371 | 0.048472 |
| 1 | 0.290830 | 0.230791 | 0.188524 | 0.143842 | 0.097114 | 0.048899 |
| 2 | 0.293393 | 0.241931 | 0.181893 | 0.139625 | 0.094943 | 0.048215 |
| 3 | 0.289288 | 0.245178 | 0.193717 | 0.133678 | 0.091410 | 0.046728 |
| 4 | 0.280369 | 0.242560 | 0.198450 | 0.146988 | 0.086950 | 0.044682 |
| 5 | 0.268094 | 0.235687 | 0.197878 | 0.153768 | 0.102306 | 0.042267 |
| 6 | 0.253604 | 0.225827 | 0.193419 | 0.155611 | 0.111500 | 0.060039 |
| 7 | 0.360232 | 0.193566 | 0.165788 | 0.133380 | 0.095572 | 0.051462 |
| 8 | 0.308771 | 0.308771 | 0.142104 | 0.114326 | 0.081919 | 0.044110 |
| 9 | 0.264660 | 0.264660 | 0.264660 | 0.097994 | 0.070216 | 0.037809 |
| 10 | 0.226852 | 0.226852 | 0.226852 | 0.226852 | 0.060185 | 0.032407 |
| 11 | 0.194444 | 0.194444 | 0.194444 | 0.194444 | 0.194444 | 0.027778 |
| 12 | 0.166667 | 0.166667 | 0.166667 | 0.166667 | 0.166667 | 0.166667 |
| 13 | 1.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 14 | 0.000000 | 1.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 15 | 0.000000 | 0.000000 | 1.000000 | 0.000000 | 0.000000 | 0.000000 |
| 16 | 0.000000 | 0.000000 | 0.000000 | 1.000000 | 0.000000 | 0.000000 |
| 17 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 | 0.000000 |
| 18 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 |
This question is asked and discussed in my forum a Wizard of Vegas.
As you know, the All bet in craps wins if every total from 2 to 12, except 7, is thrown before a 7. How many rolls on average does it take to win this bet, when it does win?
Here is my solution (PDF).
This question is asked and discussed in my forum at Wizard of Vegas.
I see somebody is claiming to have witnesses 18 consecutive yo's (total of 11) in a row at the craps table. How many rolls, on average, would it take to observe that?
Here is my solution (PDF).
A pair of two fair six-sided dice are rolled over and over until one of the following two events occur:
A) A total of 12 is rolled.
B) A total of 7 is rolled two times consecutively.
Which is more likely to happen first?
> [spoiler=Solution]
Let:
- p = Probability the 12 is rolled first from the initial state or anytime the previous roll was not a 7.
- q = Probability the 12 is rolled first when the previous roll was a 7.
This is what is known as a Markov Chain problem.
Before we get to that, recall the probability of rolling a total of 7 is 1/6 and that of a 12 is 1/36.
We can define p and q in terms of each other, as follows:
- (1) p = (1/36) + (6/36)q + (29/36)p
- (2) q = (1/36) + (29/36)p
Let's multiply equation (1) by 36:
36p = 1 + 6q + 29p
(3) 7p = 1 + 6q
Let's substitute the value for q in (2) into (3):
7p = 1 + 6*((1/36) + (29/36)p)
7p = 1 + (1/6) + (29/6)p
42p = 6 + 1 + 29p
13p = 7
q = 7/13
So, the probability of rolling the 12 first is 7/13 =~ 53.85%.
The probability of rolling two consecutive 7's first is thus 46.15%.
Thus, it's more likely the total of 12 is rolled first.





