On this page
Texas Shootout
Introduction
Texas Shootout is a simple poker based game by Galaxy Gaming. The player and dealer go against each other, the higher hand wins. The only decision is which two cards out of four to start with. The player's strengths are freedom of choice as well as the ability to split. The dealer's strength is winning on ties. If you are looking for a poker based game that is easy to play, has low volatility, and a competitive house edge then you may enjoy Texas Shootout.
Rules
- The game is played from a shoe of six ordinary 52-card decks. All hands are scored according to conventional poker rules.
- The player makes a poker bet plus an optional side bet.
- Four cards are dealt face down to both player and dealer. The player may examine his own cards.
- The player has the choice of either (A) selecting any two of his four cards and discarding the other two, or (B) splitting his hand into two 2-card hands. If the player splits then he must match the poker bet as well as the side bet, if made.
- The dealer shall turn his cards over and select two cards to start with according to the house way below, discarding the other two cards.
- The dealer shall deal five community cards.
- Both player and dealer shall make the best 5-card poker hand using any five cards from the five community cards and the two hole cards.
- If the player has the higher poker hand then the player shall win even money. If the dealer has the higher poker hand, or there is a tie, then the dealer shall win.
- The side bet shall pay according the poker value of the player's five cards and one of the pay tables below. I believe that pay table 2 is the most commonly used. In addition there is an "envy bonus" based on the poker value of all other player's at the table, as shown below.
The dealer shall play the two-card hand appearing highest on the following list. In the event that two hands of the same rank are possible, then the dealer will play the cards with the higher individual rank. An example of each hand follows each rule.
- A pair of 8's or higher. Q
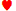 , Q
, Q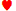
- High card is an ace and low card is jack or higher. A
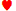 , Q
, Q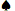
- Any suited pair 2's to 7's. 6
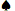 , 6
, 6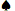
- Any unsuited pair 2's to 7's. 6
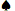 , 6
, 6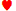
- Ace high and suited. A
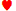 , 4
, 4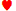
- Both cards ten or higher and suited. K
 , 10
, 10
- Both cards ten or higher and unsuited. K
 , 10
, 10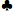
- Ace high unsuited. A
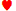 , 4
, 4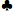
- Face card high suited. J
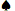 , 7
, 7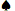
- Face card high unsuited. J
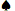 , 7
, 7
- Connected cards suited. 4
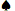 , 5
, 5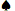
- Connected cards unsuited. 6
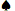 , 7
, 7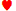
- Two highest cards suited. 8
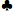 , 3
, 3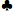
- Two highest cards unsuited. 9
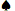 , 7
, 7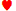
Side Bet Pay Table
| Hand | Pay Table 1 | Pay Table 2 | Pay Table 3 |
|---|---|---|---|
| Five of a kind suited | 5000 to 1 | 1000 to 1 | 1000 to 1 |
| Royal flush | 500 to 1 | 200 to 1 | 200 to 1 |
| Straight flush | 100 to 1 | 75 to 1 | 75 to 1 |
| Five of a kind | 50 to 1 | 40 to 1 | 40 to 1 |
| Four of a kind | 5 to 1 | 7 to 1 | 7 to 1 |
| Full house | 3 to 1 | 3 to 1 | 3 to 1 |
| Flush | 2 to 1 | 2 to 1 | 2 to 1 |
| Straight | 1 to 1 | 1 to 1 | 2 to 1 |
| Three of a kind | Lose | Push | Push |
Envy Bonus
| Hand | Pays |
|---|---|
| Five of a kind suited | $1000 |
| Royal flush | $250 |
| Straight flush | $50 |
| Five of a kind | $10 |
Strategy
The following strategy is not necessarily optimal. There may be penalty card situations that would marginally improve the player's odds.
The player should play the 2-card hand which appears highest on the following list. If the remaining two cards form a hand with expected value greater than zero (rank 26 or higher) then the player should split and play it as well. The expected values on this list are rough, intended only to convey the order of hands. The table below assumes the player does not make the side bet. If the player did make the side bet the strategy would indeed change.
Ranking of Two-Card Hands
| Rank | Hand | Expected Value |
|---|---|---|
| 1 | Suited A's | 0.575301 |
| 2 | Unsuited A's | 0.553041 |
| 3 | Suited K's | 0.490895 |
| 4 | Unsuited K's | 0.464249 |
| 5 | Suited Q's | 0.417272 |
| 6 | Unsuited Q's | 0.386637 |
| 7 | Suited J's | 0.345383 |
| 8 | Unsuited J's | 0.311134 |
| 9 | Suited 10's | 0.275898 |
| 10 | Unsuited 10's | 0.237068 |
| 11 | Suited 9's | 0.205034 |
| 12 | Unsuited 9's | 0.162011 |
| 13 | Suited 8's | 0.154705 |
| 14 | Suited A,K | 0.109348 |
| 15 | Unsuited 8's | 0.107616 |
| 16 | Suited 7's | 0.106813 |
| 17 | Suited A,Q | 0.069761 |
| 18 | Suited 6's | 0.05977 |
| 19 | Unsuited 7's | 0.055731 |
| 20 | Unsuited A,K | 0.053211 |
| 21 | Suited A,J | 0.033959 |
| 22 | Suited 5's | 0.013691 |
| 23 | Suited K,Q | 0.012594 |
| 24 | Suited A,10 | 0.011557 |
| 25 | Unsuited A,Q | 0.010262 |
| 26 | Unsuited 6's | 0.005561 |
| 27 | Suited K,J | -0.0187 |
| 28 | Unsuited A,J | -0.029408 |
| 29 | Suited 4's | -0.033235 |
| 30 | Suited A,9 | -0.039459 |
| 31 | Unsuited 5's | -0.04346 |
| 32 | Suited K,10 | -0.044542 |
| 33 | Unsuited K,Q | -0.048566 |
| 34 | Unsuited A,10 | -0.053852 |
| 35 | Suited A,8 | -0.060539 |
| 36 | Suited Q,J | -0.063067 |
| 37 | Suited 3's | -0.078173 |
| 38 | Suited A,7 | -0.0806 |
| 39 | Unsuited K,J | -0.082504 |
| 40 | Suited Q,10 | -0.088102 |
| 41 | Suited K,9 | -0.089785 |
| 42 | Unsuited 4's | -0.093836 |
| 43 | Suited A,6 | -0.100855 |
| 44 | Suited A,5 | -0.10132 |
| 45 | Unsuited A,9 | -0.110164 |
| 46 | Unsuited K,10 | -0.11166 |
| 47 | Suited A,4 | -0.116193 |
| 48 | Suited J,10 | -0.122052 |
| 49 | Suited 2's | -0.122698 |
| 50 | Suited K,8 | -0.124103 |
| 51 | Unsuited Q,J | -0.127974 |
| 52 | Suited Q,9 | -0.12845 |
| 53 | Suited A,3 | -0.131083 |
| 54 | Unsuited A,8 | -0.131953 |
| 55 | Suited K,7 | -0.139746 |
| 56 | Unsuited 3's | -0.142697 |
| 57 | Suited A,2 | -0.145134 |
| 58 | Unsuited A,7 | -0.154346 |
| 59 | Unsuited Q,10 | -0.155267 |
| 60 | Suited K,6 | -0.15593 |
| 61 | Suited J,9 | -0.159122 |
| 62 | Unsuited K,9 | -0.160559 |
| 63 | Suited Q,8 | -0.161784 |
| 64 | Suited K,5 | -0.170875 |
| 65 | Unsuited A,6 | -0.176551 |
| 66 | Unsuited A,5 | -0.17671 |
| 67 | Suited 10,9 | -0.180637 |
| 68 | Suited K,4 | -0.185425 |
| 69 | Unsuited J,10 | -0.189734 |
| 70 | Unsuited 2's | -0.191214 |
| 71 | Suited J,8 | -0.191644 |
| 72 | Unsuited A,4 | -0.193476 |
| 73 | Suited Q,7 | -0.194186 |
| 74 | Unsuited K,8 | -0.197604 |
| 75 | Suited K,3 | -0.199133 |
| 76 | Unsuited Q,9 | -0.199229 |
| 77 | Suited Q,6 | -0.206405 |
| 78 | Unsuited A,3 | -0.209351 |
| 79 | Suited 10,8 | -0.2107 |
| 80 | Suited K,2 | -0.213633 |
| 81 | Unsuited K,7 | -0.214514 |
| 82 | Suited 9,8 | -0.217352 |
| 83 | Suited Q,5 | -0.220169 |
| 84 | Suited J,7 | -0.223077 |
| 85 | Unsuited A,2 | -0.22489 |
| 86 | Unsuited J,9 | -0.22991 |
| 87 | Unsuited K,6 | -0.232094 |
| 88 | Suited Q,4 | -0.235311 |
| 89 | Unsuited Q,8 | -0.235583 |
| 90 | Suited 9,7 | -0.240067 |
| 91 | Suited 10,7 | -0.240998 |
| 92 | Suited 8,7 | -0.24438 |
| 93 | Unsuited K,5 | -0.248762 |
| 94 | Suited Q,3 | -0.249074 |
| 95 | Unsuited 10,9 | -0.251406 |
| 96 | Suited J,6 | -0.252745 |
| 97 | Suited Q,2 | -0.262805 |
| 98 | Suited J,5 | -0.263285 |
| 99 | Unsuited K,4 | -0.264611 |
| 100 | Unsuited J,8 | -0.265759 |
| 101 | Suited 8,6 | -0.266064 |
| 102 | Suited 9,6 | -0.266234 |
| 103 | Suited 7,6 | -0.268436 |
| 104 | Suited 10,6 | -0.270272 |
| 105 | Unsuited Q,7 | -0.270629 |
| 106 | Suited J,4 | -0.27729 |
| 107 | Unsuited K,3 | -0.279442 |
| 108 | Unsuited Q,6 | -0.283973 |
| 109 | Unsuited 10,8 | -0.284135 |
| 110 | Unsuited 9,8 | -0.290229 |
| 111 | Suited J,3 | -0.290602 |
| 112 | Suited 7,5 | -0.291758 |
| 113 | Suited 6,5 | -0.292394 |
| 114 | Suited 9,5 | -0.29242 |
| 115 | Suited 8,5 | -0.292459 |
| 116 | Unsuited K,2 | -0.295417 |
| 117 | Suited 10,5 | -0.298923 |
| 118 | Unsuited Q,5 | -0.29957 |
| 119 | Unsuited J,7 | -0.299933 |
| 120 | Suited J,2 | -0.304647 |
| 121 | Suited 10,4 | -0.309336 |
| 122 | Suited 5,4 | -0.314195 |
| 123 | Unsuited 9,7 | -0.315221 |
| 124 | Unsuited Q,4 | -0.315476 |
| 125 | Unsuited 10,7 | -0.317375 |
| 126 | Suited 6,4 | -0.318104 |
| 127 | Unsuited 8,7 | -0.318633 |
| 128 | Suited 7,4 | -0.3204 |
| 129 | Suited 8,4 | -0.321035 |
| 130 | Suited 9,4 | -0.321037 |
| 131 | Suited 10,3 | -0.322631 |
| 132 | Suited 9,3 | -0.329597 |
| 133 | Unsuited Q,3 | -0.33053 |
| 134 | Unsuited J,6 | -0.331918 |
| 135 | Suited 10,2 | -0.335747 |
| 136 | Suited 5,3 | -0.340684 |
| 137 | Suited 9,2 | -0.342481 |
| 138 | Unsuited 9,6 | -0.342769 |
| 139 | Unsuited 8,6 | -0.34313 |
| 140 | Unsuited J,5 | -0.343243 |
| 141 | Unsuited 7,6 | -0.34495 |
| 142 | Unsuited Q,2 | -0.346033 |
| 143 | Suited 6,3 | -0.347068 |
| 144 | Unsuited 10,6 | -0.348636 |
| 145 | Suited 7,3 | -0.348941 |
| 146 | Suited 8,3 | -0.349902 |
| 147 | Unsuited J,4 | -0.358831 |
| 148 | Suited 4,3 | -0.358841 |
| 149 | Suited 8,2 | -0.359102 |
| 150 | Suited 5,2 | -0.369618 |
| 151 | Unsuited 7,5 | -0.370327 |
| 152 | Unsuited 6,5 | -0.370589 |
| 153 | Unsuited 9,5 | -0.371722 |
| 154 | Unsuited 8,5 | -0.371759 |
| 155 | Unsuited J,3 | -0.373192 |
| 156 | Suited 6,2 | -0.376459 |
| 157 | Suited 7,2 | -0.377908 |
| 158 | Unsuited 10,5 | -0.37939 |
| 159 | Suited 4,2 | -0.384973 |
| 160 | Unsuited J,2 | -0.388862 |
| 161 | Unsuited 10,4 | -0.390903 |
| 162 | Unsuited 5,4 | -0.39378 |
| 163 | Unsuited 6,4 | -0.398771 |
| 164 | Unsuited 7,4 | -0.401385 |
| 165 | Suited 3,2 | -0.401451 |
| 166 | Unsuited 9,4 | -0.402623 |
| 167 | Unsuited 8,4 | -0.402719 |
| 168 | Unsuited 10,3 | -0.40569 |
| 169 | Unsuited 9,3 | -0.412853 |
| 170 | Unsuited 10,2 | -0.420634 |
| 171 | Unsuited 5,3 | -0.422846 |
| 172 | Unsuited 9,2 | -0.427508 |
| 173 | Unsuited 6,3 | -0.430175 |
| 174 | Unsuited 7,3 | -0.432623 |
| 175 | Unsuited 8,3 | -0.433916 |
| 176 | Unsuited 4,3 | -0.442055 |
| 177 | Unsuited 8,2 | -0.444371 |
| 178 | Unsuited 5,2 | -0.454349 |
| 179 | Unsuited 6,2 | -0.462125 |
| 180 | Unsuited 7,2 | -0.464479 |
| 181 | Unsuited 4,2 | -0.470729 |
| 182 | Unsuited 3,2 | -0.488024 |
Analysis
There are five possible outcomes of each initial hand. Most of the time the player will win or lose one unit. If the player splits then he can win two units, tie, or lose two units. The following table shows the probability and return of all possible net wins per initial hand. The lower right cell shows a house edge of 2.57%.
Poker Bet Return Table
| Win | Probability | Return |
|---|---|---|
| 2 | 0.026618 | 0.053236 |
| 1 | 0.437762 | 0.437762 |
| 0 | 0.032391 | 0 |
| -1 | 0.489783 | -0.489783 |
| -2 | 0.013445 | -0.026891 |
| Total | 1 | -0.025675 |
The player will split 7.25% of the time. So the element of risk is 2.57%/1.0725 = 2.39%.
The next three return tables are for the three possible pay tables of the side bet before considering the Envy Bonus. The probabilities in the tables assume the player follows the strategy above, which was designed for the player making only the poker bet. If the player made the side bet then by making strategy adjustments unknown to me the player could gain more value from the side bet at the expense of the poker bet. However, in my educated opinion the benefits of such strategy adjustments would be marginal. Unless playing at a full table that uses pay table 3, I suggest not making the side bet.
Side Bet Pay Table 1
| Hand | Pays | Probability | Return |
|---|---|---|---|
| Five of a kind suited | 5000 to 1 | 0.000001 | 0.004175 |
| Royal flush | 500 to 1 | 0.000082 | 0.040866 |
| Straight flush | 100 to 1 | 0.000203 | 0.020345 |
| Five of a kind | 50 to 1 | 0.001213 | 0.060651 |
| Four of a kind | 5 to 1 | 0.020021 | 0.100103 |
| Full house | 3 to 1 | 0.084969 | 0.254907 |
| Flush | 2 to 1 | 0.050618 | 0.101237 |
| Straight | 1 to 1 | 0.031316 | 0.031316 |
| Three of a kind | -1 to 1 | 0.098834 | -0.098834 |
| All other | -1 to 1 | 0.712743 | -0.712743 |
| Total | 1 | -0.197977 |
Side Bet Pay Table 2
| Hand | Pays | Probability | Return |
|---|---|---|---|
| Five of a kind suited | 1000 to 1 | 0.000001 | 0.000835 |
| Royal flush | 200 to 1 | 0.000082 | 0.016346 |
| Straight flush | 75 to 1 | 0.000203 | 0.015259 |
| Five of a kind | 40 to 1 | 0.001213 | 0.04852 |
| Four of a kind | 7 to 1 | 0.020021 | 0.140145 |
| Full house | 3 to 1 | 0.084969 | 0.254907 |
| Flush | 2 to 1 | 0.050618 | 0.101237 |
| Straight | 1 to 1 | 0.031316 | 0.031316 |
| Three of a kind | Push | 0.098834 | 0 |
| All other | -1 to 1 | 0.712743 | -0.712743 |
| Total | 1 | -0.104177 |
Side Bet Pay Table 3
| Hand | Pays | Probability | Return |
|---|---|---|---|
| Five of a kind suited | 1000 to 1 | 0.000001 | 0.000835 |
| Royal flush | 200 to 1 | 0.000082 | 0.016346 |
| Straight flush | 75 to 1 | 0.000203 | 0.015259 |
| Five of a kind | 40 to 1 | 0.001213 | 0.04852 |
| Four of a kind | 7 to 1 | 0.020021 | 0.140145 |
| Full house | 3 to 1 | 0.084969 | 0.254907 |
| Flush | 2 to 1 | 0.050618 | 0.101237 |
| Straight | 2 to 1 | 0.031316 | 0.062632 |
| Three of a kind | Push | 0.098834 | 0 |
| All other | -1 to 1 | 0.712743 | -0.712743 |
| Total | 1 | -0.072861 |
The final table shows the side bet house edge after factoring in the Envy Bonus. The left column is the number of players (including yourself) and the side bet pay table is along the top. This table assumes a side bet of $5. As the amount of the side bet goes up the relative value of the Envy Bonus goes down.
Side Bet House Edge with Envy Bonus
| Number of Players |
Pay Table 1 | Pay Table 2 | Pay Table 3 |
|---|---|---|---|
| 7 | 14.57% | 5.19% | 2.06% |
| 6 | 15.44% | 6.06% | 2.93% |
| 5 | 16.31% | 6.93% | 3.80% |
| 4 | 17.18% | 7.80% | 4.67% |
| 3 | 18.05% | 8.67% | 5.54% |
| 2 | 18.93% | 9.55% | 6.41% |
| 1 | 19.80% | 10.42% | 7.29% |
Methodology
I like to analyze games with a direct combinatorial analysis whenever I can. However, the number of possible combinations in this game is 2,980,936,261,442,170,000,000,000,000. Even with the best of short cuts, a perfect analysis would likely take months or years for a computer to crank through all the combinations by brute force. So, for this game, a random simulation was clearly in order. One benefit of random simulations is the analyst must quantify a strategy for the program to follow, as opposed to a brute force program which can figure out the right strategy on the fly, but then quickly forget it when the hand is over. The 2-card hand ranking strategy is what I came up with. As stated above, it may not be perfect, but if I were to figure out the penalty card exceptions the number of people in the world that would likely learn them is zero. Anybody with that kind of dedication to perfect play would likely be playing blackjack or video poker instead, in which the player can have an advantage.




