Probability - Puzzles
I am interested in finding out some specific information on the odds of rolling dice. If you have 6 dice and roll them all at once, the odds of rolling all ones are 1 in 46,656. My question is what are the odds of rolling one to five ones. I am really interested in finding out the formula that should be used to calculate this type of problem.
The probability of rolling x ones out of y dice is combin(y,x)*(1/6)x*(5/6)y-x. See my section on probabilities in poker for an explanation of the combin(x,y) function. For example the probability of rolling 4 ones is combin(6,4)*(1/6)4*(5/6)2 = 0.803755%.
Number of Ones in Six Dice
| Ones | Probability |
|---|---|
| 0 | 0.3348980 |
| 1 | 0.4018776 |
| 2 | 0.2009388 |
| 3 | 0.0535837 |
| 4 | 0.0080376 |
| 5 | 0.0006430 |
| 6 | 0.0000214 |
| Total | 1.0000000 |
Eight golfers went to a new course. The caddy master put 8 bags on four carts at random. The golfers put 8 marked golf balls in a hat. The balls were thrown in the air. The 2 closes balls to each other were partners. In every case the partners’ golf bags were already on the same cart. What is the probability of that the golf bags were paired up correctly before the throw?
The formulaic answer for the number of combinations would be combin(8,2)*combin(6,2)*combin(4,2)/fact(4) = 25*15*6/24 = 105. Another way to solve the number of combinations would be to take one golfer at random. There are 7 possible people to pair him with. Then pick another golfer at random from the six left. There are 5 possible people to pair him with. Then pick another golfer at random from the four left. There are 3 possible people to pair him with. So the number of combination is 7*5*3 = 105. Thus the answer is 1 in 105.
A friend sent me this, I was wondering if there was a formula as to how this works.
Often these mind reading number puzzles work because an interesting mathematical oddity. If the sum of digits of a number is divisible by 9 then the number it self is divisible by 9. Let’s try it on the phone number of the Las Vegas Tropicana (702-739-2222). The sum of digit is 7+0+2+7+3+9+2+2+2+2 = 36. 36 divides evenly by 9, so 702739222 must also be divisible by 9. Here is a proof of this.
- Let n bet any integer. Express n as d0*1 + d1*10 + d2*100+ d3*1000+ ... + dn*10n, where dn is the first digit, dn-1 is the second, and so on.
- n = [d0 + d1 + d2 + ... + dn ] + [d1*9 + d2*99+ d3*999+ ...+ dn*999...9 ( a number with n nines)]
- n = [d0 + d1 + d2 + ... + dn ] + 9*[d1*1 + d2*11+ d3*111+ ... dn*111...1 (a number with n ones)]
- 9*any integer is evenly divisible by 9. So if d0 + d2 + d2 + ... + dn , or the sum of digits, is divisible by 9, then the entire number must be divisible by 9.
Now that we have that proof out of the way we can look at this magic trick. The problem asks you to pick any number. Then rearrange the digits to make a second number. Then subtract the smaller number from the larger number.
The answer is always going to have a sum of digits divisible by 9. Why? For every digit in the original number it appears somewhere else in the other number. Going one set of digits at a time, changing all the other numbers to zero, we could boil down each set as +/- n*[10x - 10y] (where x>=y and n is the digit) = +/-n *10y * (10x-y - 1) = 10y * (a number composed of only nines) = a number divisible by 9.
Let’s look at an example. Let the original number be 1965. Scramble it up to get 6951. 6951 - 1965 = 6*(1000-10) + 9*(100-100) + 5*(10-1) + 1*(1-1000) = 6*990 + 9*0 + 5*9 + 6*-999. Note that each part is divisible by 9, thus the number you get after subtracting must also be divisible by 9, and finally the sum of digits is also divisible by 9.
The trick then asks you to circle a number except 0 and enter the sum of all the other digits. The program then only needs to add a number to the number you entered so that the sum is divisible by 9. For example if you said the sum of your digits was 13 then you must have circled a 5, because 13+5 = a number divisible by 9.
The reason you can’t circle a zero is because if you did and then entered a number already divisible by 9 then the program wouldn’t know whether you circled a 0 or a 9.
Great site. I refer to it often as a gambler with an interest in probability and statistics, but this question actually pertains to my work. My HR Department insists that I rate my small staff (5 people) on a bell curve--one in the top 5% of all employees, one in the next 20%, one in the next 50%, one in the next 20%, and one in the bottom 5%. The company has approximately 5000 employees. What is the probability of such a small sample size fitting this distribution?
Thanks for the compliment. This is a good problem. The probability that exactly one employee will be in the bottom 5% is 5*(.05)*(.95)4 = 0.203627. Given that one employee is in the lowest 5% the probability of exactly one in the next 20% is 4*(.2/.95)*(.75/.95)3 = 0.414361. Given these two underachievers the probability of exactly one in the next 50% out of the remaining 75% is 3*(.5/.75)*(.25/.75)2 = 0.222222. The probability that one of the remaining two falls in the lower 20% of 25% is 2*(.2/.25)*(.05/.25) = 0.32. Taking the product of all these probabilities we get 0.006, or 3/5 of 1%.
To the fellow who asked the question about order statistics (column #100), I have two quibbles: one small and one large. Your method failed to make a finite population correction, which I grant is trivial with 5000 employees, but it certainly wouldn’t have been had there been 20 employees!
More importantly, however, you implicitly assume that managers have no effect on their employees. Suppose good managers, through judicious hiring and firing, or through above-average motivational skills, raise the average level of their employees. Without accounting for this effect we will either upward- or downward-bias the resulting probabilities. I’m sure you knew this, but I am sensitized to it because I do a lot of calculations like this in discrimination cases and failure to adjust for things we can adjust for (in this case a group-specific effect) can often lead people astray.
Thank you for those good points. However the alternative to no control over the distribution of job performance ratings is rating inflation. The manager will be put in a position of giving out bloated ratings to keep his staff happy. As a government worker for ten years I speak with some experience on this. When I taught at UNLV there was no average class GPA standard but there were certain expectations about what a grading curve should look like at the end of the semester. At least in a college setting I thought that made for a reasonable policy. Perhaps in a business environment some sort of common sense medium would also be best.
Do there exist any famous unsolved problems facing gaming mathematicians? Like a Fermat's Last Theorem in the gambling world. If so, would you please share an example.
Good question. I can't think of any.
How does this work: www.1800gotjunk.com/genie/?
Let’s express your number as 10t+u. You are asked to subtract each digit, leaving you with 10t+u-t-u = 9t, a number divisible by 9. Note how all the numbers divisible by 9 have the same item, which is the one the genie predicts.
I am about to take a professional licensure examination. The regulations provide that:
- The examination shall consist of 7 subjects.
- For each subject, 60 multiple choice questions shall be asked.
- Each multiple-choice question shall have four possible answers, but only one correct answer.
- In order to pass, an examinee must obtain a general average of at least 75% and must not have a grade lower than 65% in any subject.
My question is, if an examinee merely guesses all his answers, what is his chance of passing the exam? Stated differently, what is the probability of passing the exam by sheer luck?
To satisfy the 75% requirement the student must get at least 315 out of the 420 questions right. The expected number of correct answers from guessing is 420*0.25=105. The standard deviation is (420*0.25*0.75)^0.5 = 8.87412. So the candidate must exceed expectations by 210 questions, or 210/8.87412=23.66432 standard deviations. The probability of doing this is way off the charts. If every living thing on earth took this test, answering randomly, I doubt anyone or anything would pass. I won’t even get into the other requirement.
If a university’s football team has a 10% chance of winning game 1 and a 30% chance of winning game 2, and a 65% chance of losing both games, what are their chances of winning exactly once?
If we assumed the games were independent then the probability of losing both would be 90%*70%=63%. But since you say the probability of losing both is actually 65% (which is more than the 63%), that means the two events are correlated. If the probability of losing both is 65% and just losing game 2 is 70%, then the probability of winning game 1 and losing game 2 must be 5%. Using the same logic the probability of losing game 1 and winning game 2 must be 25%. That only leaves 5% for winning both games. So the probability of winning exactly once is 25%+5% = 30%.
On the game show Let’s Make a Deal, there are three doors. For the sake of example, let’s say that two doors reveal a goat, and one reveals a new car. The host, Monty Hall, picks two contestants to pick a door. Every time Monty opens a door first that reveals a goat. Let’s say this time it belonged to the first contestant. Although Monty never actually did this, what if Monty offered the other contestant a chance to switch doors at this point, to the other unopened door. Should he switch?
Yes! The key to this problem is that the host is predestined to open a door with a goat. He knows which door has the car, so regardless of which doors the players pick, he always can reveal a goat first. The question is known as the "Monty Hall Paradox." Much of the confussion about it is because often when the question is framed, it is incorrectly not made clear the host knows where the car is, and always reveals a goat first. I think put some of the blame on Marilyn Vos Savant, who framed the question badly in her column. Let’s assume that the prize is behind door 1. Following are what would happen if the player (the second contestant) had a strategy of not switching.
- Player picks door 1 --> player wins
- Player picks door 2 --> player loses
- Player picks door 3 --> player loses
Following are what would happen if the player had a strategy of switching.
- Player picks door 1 --> Host reveals goat behind door 2 or 3 --> player switches to other door --> player loses
- Player picks door 2 --> Host reveals goat behind door 3 --> player switches to door 1 --> player wins
- Player picks door 3 --> Host reveals goat behind door 2 --> player switches to door 1 --> player wins
So by not switching the player has 1/3 chance of winning. By switching the player has a 2/3 chance of winning. So the player should definitely switch.
For further reading on the Monty Hall paradox, I recommend the article at Wikipedia.
I disagree with your answer to the Monty Hall question in the November 19, 2004 column. Assuming the car is behind door one there are actually four possibilities as follows, where the prize is behind door 1.
- Player picks door 1 --> shown 2 --> switch to 3, lose
- Player picks door 1 --> shown 3 --> switch to 2, lose
- Player picks door 2 --> shown 3 --> switch to 1, win
- Player picks door 3 --> shown 2 --> switch to 1, win
As you can see the probability of winning is 50% whether you switch or not. Furthermore it just goes against common sense that switching would be better.
Your mistake is to assume each of these events has a 25% possibility. Following is the correct probability of each event.
- Player picks door 1 (1/3) * shown 2 (1/2) = player loses (1/6)
- Player picks door 1 (1/3) * shown 3 (1/2) = player loses (1/6)
- Player picks door 2 (1/3) * shown 3 (1/1) = player wins (1/3)
- Player picks door 3 (1/3) * shown 2 (1/1) = player wins (1/3)
So losing events have a total probability of 2*(1/6) = 1/3 and winning events have a total probability of 2*(1/3)=2/3.
With five different toppings to choose from, how many different pizzas can you make, with any number of toppings?
There is 1 way with 0 toppings, 5 ways with 1 topping, 10 ways with 2 toppings, 10 ways with 3 toppings, 5 ways with 4 toppings, and 1 way with 5 toppings. So the answer is 1+5+10+10+5+1 = 32. Another way to solve is either topping can be used or not. So the total is 25 = 32.
I saw in the paper last week that the latest earthquake that ravaged Indonesia hit on December 26th. It also showed that of the eight deadliest earthquakes to hit over the last 100 years, three of them have been on December 26th. I was wondering what the odds are of having three massive quakes hit on the same day knowing these facts: Earthquakes of this magnitude (8.0 or larger) happen only once per year. The last big quake was exactly one year ago, 12/26/03 in Iran (back to back probabilities?) I look forward to hearing from you.
After discovering the claim that the Florida hurricanes only hit Bush voting counties was a hoax (see the October 17, 2004 column) I am going to be more skeptical about such alleged coincidences. According to the National Earthquake Information Center of the top 11 earthquakes since 1990 only the recent one of 2004 hit on a December 26. The Iranian earthquake you mention was only 6.7 in magnitude, which is far from making the top eight.
How many eggs do you start with if each day you sell 1/2 the eggs plus 1/2 an egg; after 3 days you have zero eggs? At the end of each day, the number of eggs is a whole number.
Let’s let d (for day) be the number of eggs at the beginning of the day and n (for night) be the number at the end. The problem tells us that d/2 - ? = n. So, let’s solve d in terms of n.
d/2 = n + ?
d= 2n + 1
So on the third day n=0, so d=1.
On the second day n=1, so d=3.
On the third day n=3, so d=7.
So there you have it, you started with 7 eggs.
Imagine a island that is inhabited by 10 people, and the politics is such that each day an islander is chosen at random to be chief for exactly one day; after the day has elapsed another islander is chosen at random (so the same islander who was just chief has a 1/10 chance of being chief again). The question to be solved: on average, how many days would have to elapse before each islander would have been chief at least once?
It will only take 1 day so that 1 person has served as chief. For the second day the probability of a new chief is 0.9. The expected number of days it will take to get a new chief, if the probability each day is 0.9 is 1/0.9 = 1.11. This is true for any probability: the expected number of trials until a success is 1/p. So after 2 people have served the probability of a new chief on the next day is 0.8. So the waiting period for a 3rd chief is 1/0.8 = 1.25 days. The answer is the sum of the waiting periods, which is 1/1 + 1/.9 + 1/.8 + ... + 1/.1 = 29.28968 days.
The radius of the circle is 1. The triangle is equilateral. Find the area of each colored region.
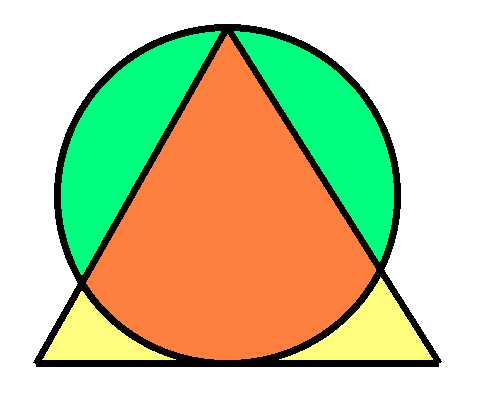
I don’t want to blow the answer for those who want to solve it for themselves. For the answer and solution visit my other web site mathproblems.info, problem 189.
Say you won a contest where at halftime of an NBA game you got to shoot a free throw and if you make it you win $1 million. Further, you can keep shooting free throws, double or nothing, till you miss or choose to stop. If you’re a 75% free throw shooter, when would you stop? Can you ever? At some point the money starts to mean less and less. What would you do?
At some point you should refuse a good bet because the stakes are too high. Personally I think a good measure of the enjoyment one gets from money is the log of the amount. The base of the log does not matter so let’s use 10. However we can’t take a log less than 10, so let’s say the enjoyment is 0 for any amount less than ten. So in your example let’s assume you have $0 before winning the $1,000,000 with your first throw. Now you have log(1,000,000) = 6 units of happiness. The expected value of your happiness taking another free throw is 0.75*log(2,000,000) + 0.25*0 = 4.975772. This is less than 6 so in this case you should take the million and walk. However it might be different if you already had some money. Let’s say you already have $200,000. Then your happiness by walking is log(1,200,000) = 6.07918. Your happiness by risking the million and taking another shot is 0.75*log(2,200,000) + 0.25*log(200,000) = 6.082075, so you marginally take the second shot. If you were to win that one your choice would be between log(2,200,000) = 6.34242 and 0.75*log(4,200,000)+0.25*log(200,000) = 6.29269. In this case you should not take a third shot and instead walk with the $2,000,000 win. The breakeven point for accepting the first double is an existing wealth of $191,487. To accept two doubles you should have $382,975 in other money.
I remember that if 22 people are in a room the odds are even that two will celebrate the same birthday [month and day, not year]. I have forgotten how to do the math to prove this. Could you please provide it.
I think I have answered this before but the 50/50 point is closer to 23. To make things simple let’s ignore leap years. The long answer is to order the 23 people somehow. The probability that person #2 has a different birthday from person #1 is 364/365. The probability person #3 has a different birthday from persons #1 and #2, assuming they are different from each other, is 363/365. Keep repeating until person 23. The probability is thus (364/365)*(363/365)*...*(343/365) = 49.2703%. So the probability of no match is 49.27% and of at least one match is 50.73%. Another solution is the number of permutations of 23 different birthdays divided by the total number of ways to pick 23 random numbers from 1 to 365, which is permut(365,23)/36523 = 42,200,819,302,092,400,000,000,000,000,000,000,000,000,000,000,000,000,000,000 / 85,651,679,353,150,300,000,000,000,000,000,000,000,000,000,000,000,000,000,000 = 49.27%.
The weekly salaries of teachers in one state are normally distributed with a mean of $490 and a standard deviation of $45. What is the probability that a randomly selected teacher earns more than $525 a week? I can’t remember how to calculate a probability from just the mean and SD without the population.
That would be $35 above average, or 7/9 standard deviations. The probability of being more than 7/9 standard deviations above expectations would be 1-Z(7/9) = 1- 0.78165 = 0.21835.
Two people are playing rock paper scissors. It is presumed the game doesn’t involve strategy. If you are playing ’best of 3’, and player A wins the first round, what are the odds that player B will win the game?
Player B would need to win the next two (not counting ties) so the probability is (1/2)*(1/2) = 1/4.
Hi, I thought I would ask you this since I cannot find it anywhere on the web. I hope you answer this; What are the odds of existing? Whether it be on Earth or somewhere else in the universe? It’s not a gambling question but an answer we should all know so we can appreciate what kind of odds we beat just being alive!
The probability that intelligent life exists anywhere in the galaxy I believe is very high. The Drake Equation seeks to estimate the number of incidents of intelligent life in the galaxy, which depending on the numbers you put into comes up with a figure of about a million. However there is also no good evidence that these civilizations have ever visited us or made contact. So the famous Fermi Question is "Where is everybody?" I do think the lack of evidence of other intelligent life casts some doubt on the Drake Equation but I would still put the number of intelligent civilizations in our galaxy in the ballpark of 1000. That is just our galaxy, there are billions of galaxies out there. However the distance between galaxies is so vast there is really not much point in discussing travel or communication between them. So to answer your question I would say roughly 99.9%.
Suppose a hotel has 10,000,000 rooms and electronic 10,000,000 keys. Due to a computer mistake each key is programmed with a random code, having a 1 in 10,000,000 chance of being correct. The hotel is sold out. What is the probability at least one customer has a working key?
The exact answer 1-(9,999,999/10,000,000)10,000,000 = 0.632121. This is also the same as (e-1)/e to seven decimal places.
There are 75 multiple choice questions in an exam. Each question contains 4 possible answers only 1 is correct. The exam pass mark is 50%. What are the chances of passing the exam by guessing each answer?
1 in 635,241.
For in-running betting, if a tennis player has a chance "p" of winning a game, what chance does he have of winning a set?
As I understand the rules of tennis the winner of a set is the first to win six games, and by a margin of at least two games, except a 6-6 tie will result in a single tie-breaker game. The following table shows the probability of winning a set, given the probability of winning a game.
Probabilities in Tennis
| Probability Game Win |
Probability Set Win |
| 0.05 | 0.000003 |
| 0.1 | 0.000189 |
| 0.15 | 0.001899 |
| 0.2 | 0.009117 |
| 0.25 | 0.028853 |
| 0.3 | 0.06958 |
| 0.35 | 0.138203 |
| 0.4 | 0.23687 |
| 0.45 | 0.361085 |
| 0.5 | 0.5 |
| 0.55 | 0.638915 |
| 0.6 | 0.76313 |
| 0.65 | 0.861797 |
| 0.7 | 0.93042 |
| 0.75 | 0.971147 |
| 0.8 | 0.990883 |
| 0.85 | 0.998101 |
| 0.9 | 0.999811 |
| 0.95 | 0.999997 |
The formula for any probability of winning a game p, and losing q, is 1*p6 + 6*p6*q + 21*p6*q2 + 56*p6*q3 + 126*p6*q4 + 252*p7*q5 + 504*p7*q6
You are in a boat with a rock, on a fresh water lake. You throw the rock into the lake. With respect to the land (shore), does the water level increase, decrease, or stay the same? My co-workers think that the water level will stay the same.
The water level relative to the shore will decrease. Inside the boat the rock is pressing down on the canoe and thus pushing up the water around it. The amount of water displaced is equal in weight to that of the rock. For example, a 10 pound rock will displace 10 pounds of water upward. When the rock is thrown overboard the weight will not matter but rather the volume of the rock. So the rock will push upward an amount of water equal in volume to the rock. The mass of a rock is greater than that of water so the rock displaces more water pushing down on it than in it. So the level of the lake will be higher with the rock in the canoe than at the bottom of the lake.
How does this work?
- Grab a calculator. (you won’t be able to do this one in your head)
- Key in the first three digits of your phone number (NOT THE AREA CODE)
- Multiply by 80
- Add 1
- Multiply by 250
- Add the last 4 digits of your phone number
- Add the last 4 digits of your phone number again.
- Subtract 250
- Divide number by 2
Do you recognize the answer?
Let’s call the first three digits in your phone number x, and the last four y. Now let’s see what I have at each step.
- Ready!
- X
- 80x
- 80x+1
- 250*(80x+1) = 20000x+250
- 20000x+250+y
- 20000x+250+2y
- 20000x+250+2y-250 = 20000x+2y
- (20000x+2y)/2 = 10000x+y
So that is of course going to equal your phone number. We need the 10000x to move the prefix four places to the left, and then we add on the last four digits.
There is a drawing for a $27,000 car, with tickets being sold at six for $500.00, or one for $100.00. 68 tickets have been sold, and tomorrow is the deadline for purchase. I know that for a 50% probability of winning, I must spend $5666.44, and for a 66.66% of winning, I must spend $11,332.88 (Right?). How much should I spend (or how many tickets must I buy) to virtually ensure that I "win" the car? (90%? 95%?) Is this raffle worth playing, or must I spend the cost of the car?
You are right regarding the 1/2 and 2/3 probabilities. If you buy t tickets your probability of winning is t/(68+t). So for a 90% probability, solve for t as follows.
0.9 = t/(68+t)
0.9*(68+t) = t
61.2 = 0.1t
t = 612, or $51,000
For 95%...
0.95= t/(68+t)
0.95(68+t) = t
64.6 = 0.05t
t = 1292, or $107,666.67
Assuming the car is worth $27,000 to you, you should quit buying tickets as soon as the next ticket sold does not increase your probability of winning enough to warrant the price.
For a ticket to be worth the price it should increase your probability of winning by p, where...
27000*p=(500/6)
p=0.003086
Let's say t is the number of tickets your purchased where you are indifferent to buying one more ticket.
[(t+1)/(t+68+1)] − [t/(t+68)] = 0.003086
[(t+1)/(t+69)] − [t/(t+68)] = 0.003086
[((t+1)*(t+68))/((t+69)*(t+68))] − [(t*(t+69))/((t+68)*(t+69))] = 0.003086
[((t2 +69t+68)/((t+69)*(t+68))] − [(t2+69t)/((t+68)*(t+69))] = 0.003086
68/((t+68)*(t+69)) = 0.003086
((t+68)*(t+69)) = 220.32
t2+137t+4692 = 22032
t2 +137t - 17340=0
t=(-137+/-(1372-4*1*-17340)2)/2
t = 79.9326
Let's test this by plugging in some values for tickets purchased, assuming the player can always buy tickets at $500/6 = $83.33 each.
At 79 tickets your cost is 79*(500/6) = $6,583.33, your probability of winning is 79/(79+68) = 53.74%, your expected return is $27,000*0.5374 = $14,510.20, and your expected profit is $14,510.20 - $6,583.33 = $7,926.87.
At 80 tickets your cost is 80*(500/6) = $6,666.67, your probability of winning is 80/(80+68) = 54.04%, your expected return is $27,000*0.5405 = $14,594.59, and your expected profit is $14,594.59 - $6,666.67 = $7,927.92
At 81 tickets your cost is 81*(500/6) = $6,750.00, your probability of winning is 81/(81+68) = 54.36%, your expected return is $27,000*0.5436 = $14,677.85, and your expected profit is $14,594.59 - $6,750.00 = $7,927.85.
So we can see that the maximum expected win peaks at 80 tickets.
I’m trying to compare the cost of replacing an old refrigerator now in order to save on electrical costs, vs. waiting until it dies to replace it. I can calculate how much cheaper it is to run the new fridge vs. the old one: $37/yr., that’s easy. But how do I factor in the cost of the new fridge? Say the new fridge costs $425. I can’t say that *all* of that $425 is a new expense, because I’ll have to replace the old fridge *someday*, if not now, so I’ll have that new-fridge expense at some point anyway. Let’s say that a typical fridge lasts 14 years and my old fridge is 9 years old, so if I replaced it now I’d be replacing it in 5 years. I tried to make a two-column table, comparing the cost of keeping the current fridge for 9 years and then replacing it, vs. replacing it now, but I didn’t know how to make an apples-to-apples comparison because I didn’t know for how far into the future to consider the costs, and because the fridges are replaced in different years. How do I compare the economics of replacing now vs. replacing later? By the way, this isn’t for my own situation, because my current fridge is probably 30 years old. It’s for, uh, a friend.
If you keep the current fridge then in five years you will have spent an extra $37*5 = $185 on electricity compared to a new one. If you replace it now you’ll be out $425 but assuming linear depreciation after five years it will still be worth $425*(9/14) = $273.21. So you will have lost $425*(5/14) = $151.79 due to depreciation. So the cost of depreciation of the new fridge is less than the additional electricity expense of keeping the old one, so I favor buying a new one now.
If there are three people, then What is the probability that at least two persons have the birthday on the same date.
Ignoring leap day, the probability of all three different birthdays is (364/365)*(363/365) = 0.99179583. So the probability of at least one common birthday is 1 - 0.99179583 = 0.00820417.
Five persons are in a room. What is the probability that at least 2 of them were born in the same birth month?
To keep things simple let’s assume that each person has a 1/12 probability of being born in each month. The probability that all five people are born in different months is (11/12)*(10/12)*(9/12)*(8/12) = 0.381944. So the probability of a common month is 1 - 0.381944 = 0.618056.
We’ve been given a challenge at work -- just for fun, and none of us can work it out. A farmer has 5 trailers full of sheep. Four of the trailers contain sheep weighing 39kg and the 5th trailer contains sheep weighing 40kg. All of the sheep are identical. He goes to the market. He wants to find out which of the trailers contains the sheep weighing 40kg, and he can only use the large weighing scales once!!! How does he do it? Please help, it is driving us all mad at my work place -- it’s a vet’s!!
The answer is at the end of the column.
Answer to sheep question
Take one sheep from trailer 1, two from trailer 2, three from trailer 3, four from trailer 4, and zero from trailer 5. If all the sheep weighed 39 kg then the total weight would be 39 * 10 = 390 kg. However 0 to 4 sheep are one kg heavier. If the total weight is 391, then there is one heavy sheep on the scale; thus it must have come from trailer 1. Likewise, if the total weight is 392, then there are two heavy sheep on the scale, which must have come from trailer 2. In the same manner a weight of 393 means the heavy sheep are in trailer 3, a weight of 394 means the heavy sheep are in trailer 4, and a weight of 390 means the heavy sheep are in trailer 5.
On an airplane with 180 seats, what are the odds of me sitting next to the good looking girl I see who will be on the same flight?
It depends on the number of seats in a cluster. Most domestic flights have three seats on either side of the aisle. That would make 60 3-seat clusters. After the first one of you is seated, there will be two seats in the same cluster out of the remaining 179, so the chances of being in the same cluster are 2/179 = 1.12%. Then you can’t have somebody else in the middle seat. The chances of the third person being in the middle seat are 1/3. So the answer is (2/179)*(2/3) = 0.74%, or 1 in 134.25.
Three logicians are playing a game. Each must secretly write down a positive integer. The logician with the lowest unique integer will win $3. If all three have the same number, each will win $1. The logicians are selfish, and each wishes to maximize his own winnings. Communication is not allowed. What strategy will each logician follow?
The answer will appear in the next column.
I read that Warren Buffet (the world’s third richest man) complained that he only paid a 17.7% federal tax rate, while his secretary paid 30%. This seems outrageous to me. Can you comment?
Normally I would say this is out of my area. However, as a former government actuary for eight years, I know a thing or two about taxes. From what I’ve read, most of Warren Buffet’s income is defined as capital gains, which is taxed at only a 15% rate. Like it or not, the tax laws allow it. What puzzled me is why his secretary was paying as much as 30%. According to this video, he was counting “payroll and income taxes.” By “payroll taxes” he obviously meant Social Security and Medicare taxes. Let’s see if 30% is a reasonable total federal tax rate for his secretary.
In 2007 the highest tax bracket was taxed at 35%, but that only applies to income above $349,700. The income up to that point is taxed much less. Let’s assume his secretary is single, with no dependent children, and her salary was $100,000. First, let’s subtract the minimum deductions. In 2007 the standard deduction for single filers was $5,350. The personal deduction was $3,400. So, we’re left with $100,000 - $5,350 - $3,400 = $91,250 in income subject to income taxes. For single filers in 2007, the tax rate was 10% on the first $7825 in income, then 15% up to $31,850, then 25% up to $77,100, and 28% up to $160,850. So, her income tax would have been =0.1×$7,825+0.15×($31,850-$7825)+0.25×($77,100-$31,850)+0.28×($91,250-$77,100) = $19,660.75. That is only 19.7% of her income. All my assumptions like her income, filing status, and not itemizing worked against her, or for a higher tax rate.
Now let’s do Social Security and Medicare. In 2007, the Social Security tax was 6.2%, up to incomes of $97,500, when it completely shuts off. The 2007 Medicare tax rate was 1.45%, with no cap. So, her combined Social Security and Medicare tax would have been 6.2%*97,500 + 1.45%*100000 = $7,495. Counting those taxes, her overall tax rate would have been ($19,660.75 + $7,495)/$100,000 = 27.2%. Still we’re 2.8% short of 30%.
My best guess is that she is also considering the fact that ultimately she is the one paying the employer’s matching Social Security and Medicare tax. For those who don’t know, Social Security and Medicare taxes are really double that deducted from your checks. The employer pays the other half. However, some, including me, would argue that ultimately it is the employee who pays both. If the employer didn’t have to pay that tax, he would have more money to pay his employees. It is easy to feel that way when you’re self-employed, like I am, and have to pay both shares. If you double the Social Security/Medicate tax, the rate is now ($19,660.75 + 2×$7,495)/$100,000 = 34.7%. I assume the 4.7% difference is because she makes less than $100,000, is married, has dependents, itemizes deductions, or some combination.
The Social Security and Medicare taxes would not apply much to Warren Buffet. First, the Social Security cap of $97,500 would be insignificant to him. Second, those taxes apply to wages, not capital gains, as he defines most of his income to be.
So, that is my best guess as to the math behind Mr. Buffet’s statement.
Update: Shortly after this column appeared I received the following response. In the interests of fairness, I present the following argument that Mr. Buffet is paying too much in taxes.
I read with interest your answer to the ’outraged’ person who thinks it is so unfair that Warren Buffet pays less percentage in taxes than his secretary. I was disappointed in your answer, which does not correct the misinformation that implies that Mr Buffet pays less tax than his secretary.First, as you noted, investment income is indeed taxed at 15%. This is in effect double taxation as the earned income that Mr. Buffet invested was taxed at his marginal rate of 36%. Comparing apples to oranges (work income vs investment income).
Second, one should not look at the percentage. In gambling terms, one should look at the ’payout’ instead. I am very certain that Mr. Buffet paid millions of dollars in taxes in the same year that his secretary paid thousands of dollars. Shouldn’t your reader be more outraged that one citizen of the country is paying 1000’s of times more than other citizens for the same government services? Once could just as easily say "I heard that Warren Buffet paid 1,000,000 times more taxes than his secretary, that is outrageous!"
Just thought I’d point out that only looking at "percentage" and not "actual payout" is a fallacy. Similar to many of your gambling fallacies.
Best Regards,
Kevin A. (Dallas)
Thank you for your entertaining collection of math puzzles. My girlfriend and I came up with this variation on the pirate puzzle. What if all the pirates are of equal rank, and in each round the proposer of the division is chosen by lot? In this variation, assume that each pirate’s highest priority is to maximize his expected amount of coins received. I have what I think is the solution, but perhaps you’d like to try your hand at it first. Thanks again.
You’re welcome. If there are only two pirates left, then the one chosen to make a suggestion has no hope, because the other pirate will vote no. The one drawn will get zero, and the other all 1000. So, before the draw, the expected value with two pirates left is 500 coins.
At the three pirate stage, the drawn pirate should suggest giving one of the other pirates 501, and 499 to himself. The one getting 501 will vote yes, because it is more than the expected value of 500 by voting no. Before the draw, with three pirates left, you have a 1/3 chance each of getting 0, 499, or 501 coins, for an average of 333.33.
At the four pirate stage the drawn pirate should choose to give 334 to any two of the other pirates, and 332 to himself. That will get him two ’yes’ votes from the pirates getting 334 coins, because they would rather have 334 than 333.33. Including your own vote, you will have 3 out of 4 votes. Before the draw, the expected value for each pirate is the average of 0, 334, 334, and 332, or 1000/4=250.
By the same logic, at the five pirate stage, the drawn pirate should choose to give 251 to any two pirates, and 498 to himself. Unlike the original problem, it isn’t necessary to work backwards. Just divide the number of coins by the number of pirates, not including yourself. Then give half of them (rounding down) that average, plus one more coin.
I need help with a puzzle called Eternity II. The prize for solving the puzzle is a staggering $2,000,000, a considerable amount of money to me. Here's a link to an interview, including the game maker himself, Christopher Monckton (former adviser to Margaret Thatcher, among many things). The game is obviously not really about gambling at all, but despite this fact, maybe you could add a word or two on your web page about it.
The game maker brags about the puzzle to be insolvable, in that link given above. I'm starting to think that he's actually right, and that he himself is the only one who will eventually become rich from selling that (ridiculous but fascinating) game. How would you, being a mathematician and all, go about solving this type of puzzle?
I hope you’re happy; I’ve been obsessed by this puzzle for the last month or so. I was lucky (or perhaps unlucky) to find the 256-piece puzzle at the local Borders book store, but I had to buy the four clue puzzles on eBay, from a guy in Australia.
I wrote a program that can easily solve the four clue puzzles. It solved the 72-piece clue puzzle #4 in less than a second. The way I did it was with a simple brute-force recursive program. I mapped out a path on the board, starting with the border. At each position, the program looped through all the unused pieces, looking for one that fit. If it found one, it moved to the next square, if it didn’t, it moved back a square.
I have had two computers crank away at the 256-piece $2 million puzzle for weeks, and neither have come anywhere close. I tend to agree with what the creator said in that video, that if you hooked up ten million of the world’s fastest computers, they still might not find the solution by the death of the universe. You would think I would have heeded his warning before starting, but in the face of a good puzzle, all consideration for practical use of my time goes out the window.
I have lots of ideas for shortcuts, but even if they sped up my program by a factor of a billion, it still probably wouldn’t help. I’m going to be extremely impressed if anybody solves this thing. What really nags at me is I feel there is some undiscovered branch of mathematics that could solve puzzles like this easily. Until then, I think glorified trial and error is the best we can do to solve it. Today’s computers are simply too slow, and the number of combinations too vast, for that to have much of a chance of success.

Suppose the distance between two cities is 1000 miles. In zero-wind, a plane can travel at 500 mph. Will it take longer to make the round trip with no wind, or a direct 100 mph tailwind in one direction, and equal head wind the other way?
In zero-wind it will take 2 hours each way, for a total of 4 hours. With the tailwind, the plane will travel at 600 mph, making the trip in 1000/600 = 1.667 hours. With the headwind, the plane will travel at 400 mph, taking 1000/400 = 2.5 hours. So, in the wind, the total time is 4.167 hours, or 10 minutes longer.
This just goes to show that it is dangerous to average averages. You can’t say the average rate of a trip is 500 mph, if it is 400 mph one way and 600 mph the other, because the 400 mph leg is over a longer period of time.
If this isn’t intuitive, consider a 500 mph wind. The plane would take 1 hour only with the wind, but it would stay in place the other way, taking forever.
I recently entered a raffle where there are 7,033 prizes and they say the odds of winning a prize are 1 in 13. I bought 5 tickets. What are my actual odds of winning something? Also, there are 40 big prizes. What are my odds of winning a big prize?
For the sake of simplicity, let’s ignore the fact that the more tickets you buy the lower the value of each ticket becomes because you compete with yourself. That said, the probability of losing all five tickets is (12/13)5 = 67.02%. So the probability of winning at least one prize is 32.98%. There are 7033×13=91,429 total tickets in the drum before you buy any. 91,429-40=91,389 are not big prizes. The probability of not winning any big prizes with five tickets is (91,389/91429)5 = 99.78%. So the probability of winning at least one big prize is 0.22%, or 1 in 458.
I have a puzzle that I’ve been trying to solve for a few months, with absolutely no progress. Time permitting, I’m hoping you can indulge me, as it’s been keeping me up at night :-). Anyway, in the glossary of Beyond Counting -- Exhibit CAA, three sequences of numbers and letters are given as the glossary entry for "Magic Numbers." One of these numbers even graces the book’s cover, so I assume they’re of some importance. Do you have any thoughts?
It isn’t often I say this, but I have no idea. As you noted in another e-mail, they take the format of serial number on US currency, two letters, with a ten-digit number in between. Out of respect for copyright, I won’t indicate what the numbers are here.
I am curious to know what became of that Eternity II puzzle challenge. Was it solved? Are you still working on it?
Thanks for asking. No, I haven’t touched that thing since I wrote about in the November 17, 2008 Ask the Wizard column. According to their web site, they will have "scrutiny dates" on December 31, 2009, and 2010 if necessary. In my opinion, it will never be solved.
Update: The Eternity II web size appears to no longer exist.
I read with fascination the Wizard's blog about Arnold Schwarzenegger’s veto letter. My question has to do with the governor’s ridiculous but predictable response. The governor stated that it was just a ’wild coincidence’. Notwithstanding the overwhelming circumstantial evidence (The bill’s sponsor and letter’s addressee was the person who had hurled insults at the governor a week earlier), do you have an estimate of what the odds are of an exactly seven-line letter spelling this phrase by chance? I think taking into account the letters used, it will be even more improbable than just assigning a 1 in 26 chance to each. It doesn't seem like U, Y, and especially K are common word-starting letters.
If you are easily offended, please skip to the next question.
For the benefit of my readers who didn’t read that blog, look at the first letter of each line in this memo by California governor Arnold Schwarzenegger (PDF), starting with the line beginning with the letter F.
This was discussed in my companion site Wizard of Vegas. To find an answer, I found a frequency of each letter of the first word in the English Language at Wikipedia.
Word Frequency by First Letter
| Letter | Frequency |
| A | 11.60% |
| B | 4.70% |
| C | 3.51% |
| D | 2.67% |
| E | 2.00% |
| F | 3.78% |
| G | 1.95% |
| H | 7.23% |
| I | 6.29% |
| J | 0.63% |
| K | 0.69% |
| L | 2.71% |
| M | 4.37% |
| N | 2.37% |
| O | 6.26% |
| P | 2.55% |
| Q | 0.17% |
| R | 1.65% |
| S | 7.76% |
| T | 16.67% |
| U | 1.49% |
| V | 0.62% |
| W | 6.66% |
| X | 0.01% |
| Y | 1.62% |
| Z | 0.05% |
To estimate the probability that Arnold’s message was indeed just a coincidence would be Prob(F) × Prob(U) × ... × prob(U) = 0.0378 × 0.0149 × 0.0351 × 0.0069 × 0.0162 × 0.0626 × 0.0149 = 1 in 486,804,391,348. This doesn’t even factor in the fact that a line break conveniently was in the place of the space between the two words.
I’d like to thank Eliot J. and Jonathan F. for their input into this solution.
At the luggage carousel in the airport, the more bags I have to retrieve the longer I can expect to wait for all of them to come out. If I have one bag, I would have to wait until about half of the bags come out. If I take 2 bags, my wait is going to be longer and with 3, longer still. Assuming my bags are mixed up randomly among the others, what is a general formula for number of bags I’ll have to wait to come out to get all my bags, in terms of my number of bags and the total number of bags?
Let’s define some variables first, as follows:
n = number of your bags
b = total number of bags
As the number of total bags gets larger the answer will get closer to b×n/(n+1). For a large plane, that will give you a good estimate. However, if you want to be exact, the answer is
[b×combin(b,n)-(sum for i=n to b-1 of combin(i,n))]/combin(b,n)
For example, if there are 10 total bags, and four of them are yours, then the expected wait time =
[10×combin(10,4)-combin(4,4)-combin(5,4)-combin(6,4)-combin(7,4)-combin(8,4)-combin(9,4)]/combin(10,4) = 8.8 bags.
Solution:
The number of ways to pick n out of b bags is combin(b,n). So, the probability that all your bags come out within the first x bags is combin(x,n)/combin(b,n). The probability that your last bag is the xth bag to come out is (combin(x,n)-combin(x-1,n))/combin(b,n), for x>=n+1. For x=n it is 1/combin(b,n).
So, the ratio of the expected wait time to the total wait time is:
n×combin(n,n)/combin(b,n) +
(n+1)×(combin(n+1,n)-combin(n,n))/combin(b,n) +
(n+2)×(combin(n+2,n)-combin(n+1,n))/combin(b,n) +
.
.
.
+
(b-1)×(combin(b-1,n)-combin(b-2,n))/combin(b,n) +
b×(combin(b,n)-combin(b-1,n))/combin(b,n)
Taking a telescoping sum, this can be simplified to:
[b×combin(b,n)-combin(b-1,n)-combin(b-2,n)-...-combin(n,n)]/combin(b,n)
A reader later wrote in saying that the answer can be simplified to n×(b+1)/(n+1). This can be shown by induction, a legitimate method, but always leaves me emotionally unsatisfied.
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
I sell sculptures. On average, out of every seven sculpture sales, one will be a turtle, and the rest will be other types of sculptures. How many turtles do I need to have in stock if I want a 90% chance of not running out in the next 100 sculpture sales?

Let t be the number of turtles made, and x the number sold.
pr(x<=t)=0.9
pr(x-14.29<=t-14.29)=0.9
pr((x-14.29)/3.5)<=(t-14.29)/3.5))=0.9
The left side of the inequality follows a standard normal distribution (mean of 0, standard deviation of 1). This next step takes an introductory statistics course, or some faith, to accept.
(t-14.29)/3.5 = normsinv(0.9) This is the Excel function.
(t-14.29)/3.5 = 1.282
t-14.29 = 4.4870
t = 18.77
Nobody is likely to buy 0.77 of a turtle statue, so I would round up to 19. According to the binomial distribution, the probability of selling 18 or less is 88.35%, and 19 or less is 92.74%. This question was raised and discussed in the forum of my companion site Wizard of Vegas.
Five sailors survive a shipwreck. The first thing they do is gather coconuts and put them into a big community pile. They meant to divide them up equally afterward, but after the hard work gathering the coconuts, they are too tired. So they go to sleep for the night, intending to divide up the pile in the morning.
However, the sailors don’t trust one another. At midnight one of them wakes up to take his fair share. He divides up the pile into five equal shares, with one coconut left over. He buries his share, combines the other four piles into a new community pile, and gives the remaining coconut to a monkey.
At 1:00 AM, 2:00 AM, 3:00 AM, and 4:00 AM each of the other four sailors does the exact same thing.
In the morning, nobody confesses what he did, and they proceed with the original plan to divide up the pile equally. Again, there is one coconut left over, which they give to the monkey.
What is the smallest possible number of coconuts in the original pile?
"Scroll down 100 lines for the answer.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
There were 15,621 coconuts in the original pile. Scroll down another 100 lines for my solution.
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
Let c be the number of coconuts in the original pile and f be the final share for each sailor after the last division.
After sailor 1 takes his share and gives the monkey his coconut there will be (4/5)×(c-1) = (4c-1)/5 left.
After sailor 2 takes his share and gives the monkey his coconut there will be (4/5)×(((4c-1)/5)-1) = (16c-36)/25 left.
After sailor 3 takes his share and gives the monkey his coconut there will be (4/5)×(((16c-36)/25)-1) = (64c-244)/125 left.
After sailor 4 takes his share and gives the monkey his coconut there will be (4/5)×(((64c-244)/125)-1) = (256c-1476)/625 left.
After sailor 5 takes his share and gives the monkey his coconut there will be (4/5)×(((256c-1476)/625)-1) = (1024c-8404)/3125 left.
In the morning each sailor’s share of the remaining pile will be f = (1/5)×(((1024c-8404)/3125)-1) = (1024c-11529)/15625 left.
So, the question is what is the smallest value of c such that f=(1024×c-11529)/15625 is an integer. Let’s express c in terms of f.
(1024×c-11529)/15625 = f
1024c - 11529 = 15625×f
1024c = 15625f+11529
c = (15625f+11529)/1024
c = 11+((15625×f+265)/1024)
c = 11+15×f+(265×(f+1))/1024
So, what is the smallest f such that 265×(f+1)/1024 is an integer? 265 and 1024 do not have any common factors, so f+1 by itself is going to have to be divisible by 1024. The smallest possible value for f+1 is 1024, so f=1023.
Thus, c = (15625×1023+11529)/1024 = 15,621.
Here is how many coconuts each person, and monkey, received:
Coconut Problem
| Sailor | Coconuts |
| 1 | 4147 |
| 2 | 3522 |
| 3 | 3022 |
| 4 | 2622 |
| 5 | 2302 |
| Monkey | 6 |
| Total | 15621 |
David Filmer, the one who challenged me the with question, already knew the answer. Actually, he asked me the formula for the general case of s sailors, but I had enough trouble with the specific case of 5 sailors. David notes the answer for the general case is c = ss+1 - s + 1.
I’ll leave that proof to the reader.
Here are some links to alternate solutions to the problem:
A man is presented with two envelopes full of money. One of the envelopes contains twice the amount as the other envelope. Once the man has chosen his envelope, opened and counted it, he is given the option of changing it for the other envelope. The question is, is there any gain to the man in changing the envelope?
It would appear that by switching the man would have a 50% chance of doubling his money should the initial envelope be the lesser amount and a 50% chance of halving it if the initial envelope is the higher amount. Thus, let x be the amount contained in the initial envelope and y be the value of changing it:
y = 0.5×(x/2) + 0.5×(2x) = 1.25x
Let’s say that the initial envelope contained $100. So there should be a 50% chance that the other envelope contains 2 × $100 = $200 and a 50% chance that the other envelope contains (1/2) × $100 = $50. In such a case, the value of the envelope is:
0.5×($100/2) + 0.5×(2×$100) = $125
This implies that the man would, on average, increase his wealth by 25% simply by switching envelopes! How can this be?
This appears to be a mathematical paradox, but is really just an abuse of the expected value formula. As you noted in the question, it seems like the other envelope should have 25% more than the one you chose. However, if you buy that, then you may as well pick the other envelope to begin with. Furthermore, you could use that argument to switch back and forth forever if you don’t get to open the envelopes before deciding to switch. Clearly there must be some flaw in the expected value argument. The question is, where is the flaw?
I have spent a lot of time reading about this problem and discussing it over the years. I’ve heard and read many explanations about why the y=.5x + .5*2x = 1.25x argument is wrong. Many have used many pages of advanced mathematics in the explanation, which I don’t think is necessary. It is a simple question that calls out for a simple answer. So, this is my crack at it.
You must be very careful with what you do with the stated fact that one envelope has twice the money as the other one. Let’s call the amount in the smaller envelope S, and the larger one L. So we have:
L=2×S
S=0.5×L
Notice how the 2 and 0.5 factors are applied to different envelopes. You can’t take both factors and apply them to the same amount. If the first envelope has $100 then if it was the smaller envelope, the other one will have $200. If the $100 was the larger envelope, then the other one will have $50. So the other envelope will have $50 or $200. However, you can’t jump from there to say there is a 50/50 chance of each. This is because that would be applying the 0.5 and 2 factors to the same amount, which you can’t do. Without knowing the prize distribution to begin with, you can’t assign possible amounts to the second envelope.
If the 0.5x/2x argument is wrong, then what would be the correct way to set up the expected value of the other envelope? The way I would do it is to say that the difference between the two envelopes is L-S = 2S-S = S. By switching you’ll either gain or lose S, whatever it is. If the two envelopes have $50 and $100, then switching will gain or lose $50. If the two envelopes have $100 and $200, then switching will gain or lose $100. Either way, the expected gain by switching is 0. I think I could say that if the first envelope has $100, then there is a 50% chance the difference in the other envelope is $50, and a 50% chance it is $100. So the expected difference is $75. Thus, the expected value of the other envelope is 0.5×($100+$75) + 0.5×($100-$75) = 0.5×($175+$25) = $100.
I hope that makes some sense. This problem always induces lots of comments. If you have one, please don’t write to me directly, but post it in my Wizard of Vegas forum. The link is below.
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
Links
Consider a truel (a three-way duel) with participants A, B, and C. They are fighting to the death over a woman. They are all gentlemen, and they all agree to the following rules.
- The three participants form a triangle.
- Each has one bullet only.
- A goes first, then B, and C.
- A’s probability of hitting an intended target is 10%.
- B’s probability of hitting an intended target is 60%.
- C’s probability of hitting an intended target is 90%.
- There are no accidental shootings.
- Shooting in the air (deliberately missing) and shooting yourself is allowed, and are always successful.
- If two or three survivors remain after any round, then each is given a new bullet. They will then repeat taking turns shooting, in the same order, skipping anybody who already died.
- All three participants are perfect logicians.
Who should A aim at initially? What is his probability of survival for each initial target?
This puzzle is discussed on the BBC show Quite Interesting. Scroll down 100 lines for the answer and solution.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
Here are my probabilities of A winning according to each initial target. As you can see, A’s probability of winning is maximized by deliberately firing in the air.
Truel Odds
| Strategy | Prob. Win |
| Air | 13.887% |
| A | 0.000% |
| B | 12.560% |
| C | 13.094% |
For the solution, let’s use the notation Pr(X) to denote the probability of group X, and only group X, remains after a round. Let’s use the terminololy Pr(X*) to denote the probability of group X eventually winning the round, after repeating until the game state changes by somebody getting hit. Let Pr(X**) be the probability that player X is the sole survivor. To find the final probabilities, let’s look at the two-player states first. It is obvious that each will shoot at the other.
A vs. B
- Pr(A) = 0.1
- Pr(B) = 0.9×0.6 = 0.54
- Pr(AB) = 0.9×0.4 = 0.36
If both survive then they will repeat until there is one survivor only. So the probabilities of being the final survivor are:
- Pr(A*) = Pr(A)/(1-Pr(AB)) = 0.1/0.64 = 0.15625
- Pr(B*) = Pr(B)/(1-Pr(AB)) = 0.54/0.64 = 0.84375
A vs. C
- Pr(A) = 0.1
- Pr(C) = 0.9×0.9 = 0.81
- Pr(AC) = 0.9×0.1 = 0.09
If both survive then they will repeat until there is one survivor only. So the probabilities of being the final survivor are:
- Pr(A*) = Pr(A)/(1-Pr(AC)) = 0.1/0.91 = 0.10989011
- Pr(C*) = Pr(B)/(1-Pr(AC)) = 0.81/0.91= 0.89010989
B vs. C
- Pr(B) = 0.6
- Pr(C) = 0.4×0.9 = 0.36
- Pr(BC) = 0.$×0.1 = 0.04
If both survive then they will repeat until there is one survivor only. So the probabilities of being the final survivor are:
- Pr(B*) = Pr(A)/(1-Pr(BC)) = 0.6/.96 = 0.625
- Pr(C*) = Pr(B)/(1-Pr(BC)) = 0.36/.96= 0.375
Now we’re ready to analyze the three-player case. Let’s consider the situation where A aims at B.
Three Player — A Aims at B
If A hits B then C will definitely survive, and may or may not hit A. So two possible outcomes of hitting B are AC and C. If A misses B then B will aim at the greater threat C. If B hits C then A and B will survive. If B misses C then C will aim at the greater threat B. If C misses B then all three will survive. If C hits B then A and C will survive. So the possible outcomes are C, AB, AC, and ABC.
- Pr(A) = 0.
- Pr(B) = 0.
- Pr(C) = 0.1 × 0.9 = 0.09. This is achieved by A hitting B, and then C hitting A.
- Pr(AB) = 0.9 × 0.6 = 0.54. This is achieved by A missing B, and then B hitting C.
- Pr(AC) = 0.1 × 0.1 + 0.9 × 0.4 × 0.9 = 0.334. This can be achieved two ways. The first is A hitting B, and then C missing A. The second is A missing B, B missing C, and then C hitting B.
- Pr(BC) = 0.
- Pr(ABC) = 0.9 × 0.4 × 0.1 = 0.036. This is achieved by all three missing.
By the same logic as the two-player cases, we can divide each outcome by (1-Pr(ABC))=0.964 to find the probabilities of each state, assuming that the state of the game did change after the round.
- Pr(C*) = 0.09/0.964 = 0.093361.
- Pr(AB*) = 0.54/0.964 = 0.560166.
- Pr(AC*) = 0.334/0.964 = 0.346473.
From the two-player cases, we know if it comes down to A and B then A will win with probability 0.15625, and B 0.84375. If it comes down to A and C then A will win with probability 0.109890, and C 0.890110.
- Pr(A**) = (0.560165975 × 0.15625) + (0.346473029 × 0.10989011) = 0.125600. A can be the winner two ways: (1) getting to the AB state, and then winning, or (2) getting to the AC state and then winning.
- Pr(B**) = 0.560166 × 0.84375 = 0.472640. B will be the winner if it gets to the AB state, and then B wins.
- Pr(C**) = 0.093361 + (0.346473 × 0.890110) = 0.401760. C can win by A killing B, and then C killing A in the first round, or by it getting to state AC, and then C winning.
So, if A’s strategy is to aim at B at first, then his probability of being the sole survivor is 12.56%.
Three Player — A Aims at C
If A hits C then B will definitely survive, and may or may not hit A. So two possible outcomes of hitting C are AB and B. If A misses C then B will aim at the greater threat C. If B hits C then A and B will survive. If B misses C then C will aim at the greater threat B. If C misses B then all three will survive. If C hits B then A and C will survive. So the possible outcomes are B, AB, AC, and ABC.
- Pr(A) = 0.
- Pr(B) = 0.1 × 0.6 = 0.06.
- Pr(C) = 0.
- Pr(AB) = (0.1 × 0.4) + (0.9 × 0.6) = 0.04+0.54 = 0.58. This can be achieved two ways. The first is A hitting C, and then B missing A. The second is A missing B, and then B hitting C.
- Pr(AC) = 0.9 × 0.4 × 0.9 = 0.324. This is achieved by A missing C, B missing C, and C hitting B.
- Pr(BC) = 0.
- Pr(ABC) = 0.9 × 0.4 × 0.1 = 0.036. This is achieved by all three missing.
By the same logic as the two-player cases, we can divide each outcome by (1-Pr(ABC))=0.964 to find the probabilities of each state, assuming that the state of the game did change after the round.
- Pr(B*) = 0.06/0.964 = 0.062241.
- Pr(AB*) = 0.58/0.964 = 0.601660.
- Pr(AC*) = 0.324/0.964 = 0.336100.
By the same logic as the solution for the A aims at B case:
- Pr(A**) = (0.601660 × 0.15625) + (0.336100 × 0.10989011) = 0.130943.
- Pr(B**) = 0.062241 + 0.601660 × 0.84375 = 0.569891.
- Pr(C**) = 0.336100 × 0.890110 = 0.299166.
So, if A’s strategy is to aim at C at first, then his probability of being the sole survivor is 13.09%.
Three Player — A Misses Deliberately
After A deliberately misses then B will aim at the greater threat C. If B hits C then A and B will survive. If B misses C then C will aim at the greater threat B. If C misses B then all three will survive. If C hits B then A and C will survive. So the possible outcomes are AB, AC, and ABC.
- Pr(A) = 0.
- Pr(B) = 0.
- Pr(C) = 0.
- Pr(AB) = 0.6. This is achieved by B hitting C.
- Pr(AC) = 0.4 × 0.9 = 0.36. This is achieved by B missing C, and then C hitting B.
- Pr(BC) = 0.
- Pr(ABC) = 0.4 × 0.1 = 0.04. This is achieved by all three missing.
By the same logic as the two-player cases, we can divide each outcome by (1-Pr(ABC))=0.96 to find the probabilities of each state, assuming that the state of the game did change after the round.
- Pr(AB*) = 0.6/0.96 = 0.625.
- Pr(AC*) = 0.36/0.96 = 0.375.
By the same logic as the solution for the A aims at B case:
- Pr(A**) = (0.625 × 0.15625) + (0.375 × 0.109890) = 0.138865.
- Pr(B**) = 0.625 × 0.84375 = 0.527344.
- Pr(C**) = 0.375 × 0.890110 = 0.333791.
So, if A’s strategy is to aim at C at first, then his probability of being the sole survivor is 13.89%.
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
Comparing two elements at a time, what is the fastest way to sort a list, minimizing the maximum number of comparisons?
There are several ways that are about equally as good. However, the one I find the easiest to understand is called the merge sort. Here is how it works:
- Divide the list in two. Keep dividing each subset in two, until every subset is size 1 or 2.
- Sort each subset of 2 by putting the smaller member first.
- Merge pairs of subsets together. Keep repeating until there is just one sorted list.
The way to merge two lists is to compare the first member of each list, and put the smaller one in a new list. Then repeat, and put the smaller one after the smaller member from the previous comparison. Keep repeating until the two groups have been merged into one sorted group. If one of the original two lists is empty, then you can append the other list to the end of the merged list.
The following table shows the maximum number of comparisons necessary according to the number of elements in the list.
Merge Sort
| Elements | Maximum Comparisons |
| 1 | 0 |
| 2 | 1 |
| 4 | 5 |
| 8 | 17 |
| 16 | 49 |
| 32 | 129 |
| 64 | 321 |
| 128 | 769 |
| 256 | 1,793 |
| 512 | 4,097 |
| 1,024 | 9,217 |
| 2,048 | 20,481 |
| 4,096 | 45,057 |
| 8,192 | 98,305 |
| 16,384 | 212,993 |
| 32,768 | 458,753 |
| 65,536 | 983,041 |
| 131,072 | 2,097,153 |
| 262,144 | 4,456,449 |
| 524,288 | 9,437,185 |
| 1,048,576 | 19,922,945 |
| 2,097,152 | 41,943,041 |
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
On October 29, 2010, the The Las Vegas Review Journal published a poll in the Reid-Angle Senate race. It said that on a survey of 625 likely voters, Angle won 49% and Reid won 45%. It also said the margin of error was 4%. Here are my questions:
- What is Angle’s probability of winning?
- What would be a 95% confidence interval for Angle’s share of the vote?
- What does the margin of error mean?
My apologies for the dated reply on this. I wrote the following before the election.
First, I’m going to get rid of that other 6%, who are either undecided or will waste their votes on a third party candidate or "none of the above," which is an option in Nevada. Some may disagree with this assumption. To be honest, another reason for ignoring them is the math gets more complicated with more than two candidates. So, after rounding, that would leave us with 306 votes for Angle, and 281 votes for Reid, for a total of 587 in the sample.
I’m going to use the standard normal approximation to answer this question. If I were going to be a perfectionist, then I would use the T distribution, because the actual mean and variance are not known. However, in my opinion, a sample size of 587 is perfectly fine for the normal distribution.
Sample size = 306+281 = 587.
Angle sample mean is 306/587 = 0.521295.
The estimated standard deviation of the mean is (0.521295 × 0.478705 / (587-1))^0.5 = 0.0206361.
Angle’s share above 50% is (0.521295-0.5)/0.0206361 = 1.031917 standard deviations.
According to the normal distribution, the probability of Reid finishing 1.031917 standard deviations above expectations is 0.151055. This can be found in Excel with the function NORMSDIST(-1.031917). So Angle’s probability of winning is 1-0.151268 = 84.89%.
To create a 95% confidence interval, note that the 2.5% point on either side of the Gaussian curve is at 1.959964 standard deviations from the mean. This can be found in Excel with the function NORMSINV(0.975). As already noted, the estimated standard deviation of the sample mean is 0.0206361. So there is a 95% chance that either candidate will get within 0.0206361×1.959964 = 0.040446 standard deviations of the poll results. So Angle’s 95% confidence interval is 0.521295 +/- 0.040446 = 48.08% to 56.17%.
I’m told it would be mathematically incorrect to phrase that as "Angle’s share of all Angle/Reid votes has a 95% chance of falling between 48.08% and 56.17%." That was how I originally phrased my answer, but two statisticians recoiled in horror at my wording. To paraphrase their response, they said I had to use the passive voice, and say that "48.08% and 56.17% will surround Angle’s share with 95% probability." To be honest with you, it sounds the same to me. However, they stressed that the confidence interval is random and Angle’s share is immutable, and that my original wording implied the opposite. Anyway, I hope the frequentist statisticians out there will be satisfied with the second wording.
The "margin of error" is half the difference between the two ends of the 95% confidence interval. In this case (56.17% - 48.08%)/2 = 4.04%.
As a follow-up, here are the actual results:
Reid: 361,655
Angle: 320,996
Other: 21,979
So, not counting the "other" votes, Reid got 53.0% and Angle 47.0%. That is a comfortable 6% win for Reid. It begs the question of why the poll was so far off. Was it chance? Did voters change their minds? Or was it a bad poll to begin with? I leave those questions to the reader (I hate it when textbooks say that).
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
I tried your actuarial calculator. Why is it that the probability of reaching my expected age at death is less than 50%?
You’re confusing the mean and the median. Let’s look at my situation as an example. I’m a 45-year-old male. My life expectancy is 78.11 years, yet I have a 50.04% chance of making it to age 80.
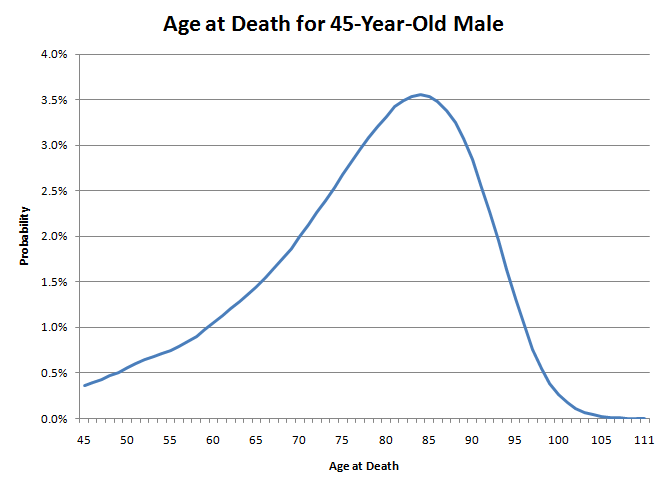
My age at death will be like throwing a dart at this graph. Notice how the left tail is a lot fatter than the right. That means my probability of death right now is quite low. However, as I get older, the probability of death in the next year will keep getting higher. For example, for a 45-year-old male the probability of surviving to 46 is quite high at 99.64%. However, at age 85 the probability of making it to 86 is 89.21% only. It is like nature slowly pushing a knife in your back. At first it probably won’t kill you, but with each passing year, the odds slowly increase that it will. However, once you get to the late seventies nature says enough with the games and really starts shoving it in.
So if a lot of 45-year-old men throw darts at this graph, 49.96% will hit between 45 and 79, and 50.04% will hit between 80 and 111. However, the lucky half who make it on the right side of the graph will probably not live much past 80. Once a male reaches 80 he can expect to live 7.78 more years only. Meanwhile, many in the unlucky half who don’t make it to 80 will die much younger than that. So it is the many young deaths that pull down average life expectancy.
For a similar situation, consider a die numbered 10, 20, 30, 31, 32, 33. The average is 26, yet there is a 2/3 chance of rolling more than that.
As an example of how the mean and median are different, suppose we add two more deaths to the sample. One death at 46 and one at 81. The probability of making it to 80 doesn’t change, but the average life expectancy at age 45 would go down.
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
Imagine an infinitely elastic rubber band that is 1 km. long unstretched. It expands at a rate of 1 km. per second. Next, imagine an ant at one end of the rubber band. At the moment the rubber band starts expanding the ant crawls towards the other end at a speed, relative to his current position, of 1 cm. per second. Will the ant ever reach the other end? If so, when?
Yes, it will, after e100,000 -1 seconds. See my mathproblems.info site, problem 206, for two solutions.
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
Do you think the better fuel efficiency is worth the additional cost of a hybrid? How many miles would you have to drive to break even?
Good question. To answer it I considered a Toyota Highlander, a vehicle I am thinking of purchasing. The retail cost of the standard hybrid model is $37,490. For the same four-wheel-drive vehicle non-hybrid the cost is $29,995. So the hybrid engine adds $7,495 to the cost.
The gas mileage of the hybrid is 28 mph, both city and highway. The mileage of the non-hybrid is 17 city and 22 highway. Let’s take the average at 19.5.
The general formula for the number of miles to break even is h×mh×mr/(g×(mh-mr)), where
h = Additional cost of the hybrid.
g = Cost for a gallon of gas.
mr = Mileage for non-hybrid (the "r" is for a regular car).
mh = Mileage for a hybrid.
The following table uses this formula to find the break even point for various prices of gas from $2 to $5 per gallon.
Hybrid Break Even Point
| Cost of Gas | Number of Miles |
| $2.00 | 240,722 |
| $2.25 | 213,975 |
| $2.50 | 192,577 |
| $2.75 | 175,070 |
| $3.00 | 160,481 |
| $3.25 | 148,136 |
| $3.50 | 137,555 |
| $3.75 | 128,385 |
| $4.00 | 120,361 | $4.25 | 113,281 |
| $4.50 | 106,987 |
| $4.75 | 101,357 |
| $5.00 | 96,289 |
So, at the current price of $3.00 per gallon here in Vegas, you would need to put more than 160,481 miles on the vehicle to come out ahead. This does not consider other expenses that may be associated with a hybrid, such as the expensive replacement cost of batteries, nor any perceived green points for consuming less fossil fuel.
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
What ratio of genes would I have in common with a full brother or sister, other than identical twin?
1/2.
If we used keno as a comparison, everybody would have 40 genes, each represented by a keno ball. However, each ball would have unique number. When two people, who are not related, mate it is like combining 80 balls between the two of them into a hopper, and randomly choosing 40 genes for the offspring of the mating.
So when you were conceived, you got half the balls in the hopper, and the other half were wasted. When your brother or sister was conceived he/she got half from the balls drawn when you were born, and half that were not drawn. So you are 50% genetically identical. Much for the same reason that if 40 numbers were drawn in keno, two consecutive draws would average 20 balls in common.
This question was raised and discussed in the forum of my companion site Wizard of Vegas.
A factory that produces tables and chairs is equipped with 10 saws, 6 lathes, and 18 sanding machines. It takes a chair 10 minutes on a saw, 5 minutes on a lathe, and 5 minutes of sanding to be completed. It takes a table 5 minutes on a saw, 5 minutes on a lathe, and 20 minutes of sanding to be completed. A chair sells for $10 and a table sells for $20. How many tables and chairs should the factory produce per hour to yield the highest revenue, and what is that revenue?
Let’s let c stand for the number of chairs made per hour, and t the number of tables. Revenue per hour will be 10×c + 20×t.
The 10 saws result in 600 minutes of sawing per hour. We were given that it takes a chair 10 minutes of saw time, and a table 5. So that limits hour hourly production to:
(1) 10c + 5t <= 600
The 6 lathes result in 360 minutes of lathing per hour. We were given that it takes a chair 5 minutes of saw time, and a table 5. So that limits hour hourly production to:
(2) 5c + 5t <= 360
The 18 sanding machines result in 1080 minutes of sanding per hour. We were given that it takes a chair 5 minutes of saw time, and a table 20. So that limits hour hourly production to:
(3) 5c + 20t <= 1080
The following graph shows the three constraints placed by the three sets of machinery. The factory may produce any combination of chairs and tables that is under all three lines. The question is where under the three lines results in the greatest revenue.
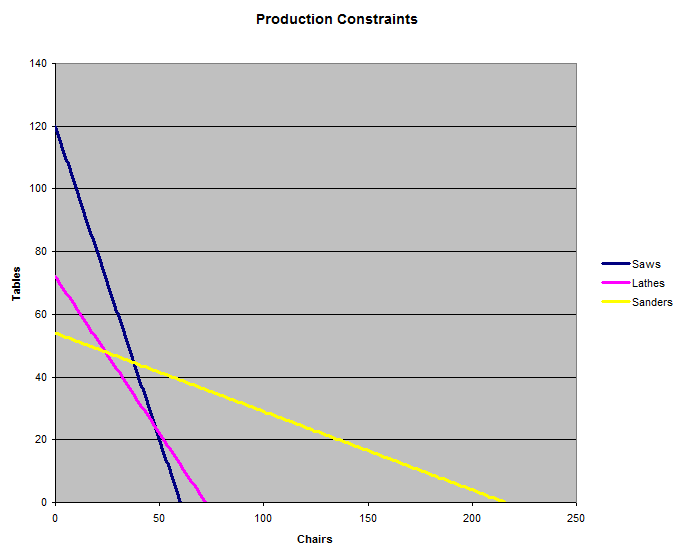
It stands to reason that the answer would be the intersection of two lines, make all chairs, or make all tables. So let’s find where the lines intersect. First, let’s find where equation (1) and (2) intersect. We can change the <= expression to just =, to use the machines to their maximum potential.
(1) 10c + 5t = 600
(2) 5c + 5t = 360
Subtract (2) from (1):
5c = 240
c = 48
Plugging 48 for c into equation (1):
10×48 + 5t = 600
5t = 120
t = 24
So, equations (1) and (2) meet at 48 chairs and 24 tables.
Next, let’s find where equations (2) and (3) meet:
(2) 5c + 5t = 360
(3) 5c + 20t = 1080
Subtracting (2) from (3):
15t = 720
t = 48
Putting that into (2) or (3) we can solve for c, which is 24.
So, equations (2) and (3) meet at 24 chairs and 48 tables.
We don’t need to bother finding where equations (1) and (3) meet, because we can see from the graph that where the saw and sanders lines meet is outside of the lathe constraint.
It is also possible that making chairs only is the right answer. The graph shows that the saws is the biggest limitation to making only chairs. From equation (1) if we put in 0 for the number of tables we get c=60.
Another possibility is making tables only. The graph shows that the sanders will be the biggest limitation. Putting in 0 chairs into equation (3) we find we can make no more than 54 tables.
The following graph shows the total revenue for each viable answer. Remember, the revenue is $10 per chair and $20 per table.
Total Hourly Revenue
| Chairs | Tables | Revenue |
| 0 | 54 | $1,080 |
| 24 | 48 | $1,200 |
| 48 | 24 | $960 |
| 60 | 0 | $600 |
The king has a barrel full of wine.
On Monday night, a servant steals three cups from the barrel and replaces them with three cups of water.
On Tuesday night another servant steals three cups from the now diluted barrel of wine and replaces them three cups of water.
On Wednesday night yet another servant steals three cups from the now-more diluted barrel of wine and replaces them three cups of water.
On Thursday morning the barrel is 50% wine and 50% water.
How much wine was initially in the barrel?
Here is the answer and solution (PDF).
For discussion about this problem, please visit my forum at Wizard of Vegas.
If I had a bowl of 200 Skittles and 3 would kill me, what are the chances I would die if I took a handful of 12 and ate all of them. Assume that it takes only one poison Skittle to kill me.
For more discussion on this question, please visit my forum at Wizard of Vegas.
An alien has abducted ten logicians and placed them in a room. He explains to them that he first order them in a line, from tallest to shortest, with each person facing the direction of the next shortest person in front, so that each person may see all shorter logicians, but no taller ones. He then explains that he will place a black or white hat on each person, however nobody will be able to see the color of his own hat, only the hats of the shorter logicians. The distribution of black and white hats could be anything, not necessarily five and five.
The alien then explains that he will ask each logician, starting with the tallest, and moving down the line, the color of his hat. The logicians may hear the response of those acting before them. Other than the black/white responses, they may not communicate in any way once the game has started. If more than one logician is wrong, then they will all be eaten. If at least nine answers are correct, they will be returned safely to earth. The alien then gives them some time to strategize. What should their strategy be?
Following is one possible strategy. Have the first logician to act say "black" if he sees an even number of black hats and "white" for an odd number on the other nine logicians. He will have a 50% chance of matching the color of his own hat, so he is the only one allowed to be wrong. Whatever he says, define that as the "running color."
Next, the second logician to act will take a count of the black hats on the shorter eight logicians and match it to a color by the same odd and even method as the first logician. If this agrees with the color stated by the first logician, then he must have a white hat, and he should state white. If it disagrees, he must have a black hat, and should state black. If he says "white," then the running color will stay the same. If he says "black," then the running color will flip to the opposite color.
Next, the third logician to act will do exactly as the second one, but taking a count of the black hats on the seven shorter logicians. Likewise, if he agrees with the running color, he will say "white" and the running color stays the same. If he disagrees with the running color, he will say "black" and the running color will flip.
Each of the other logicians will do exactly the same thing.
Of course, they could just as easily associate black to an odd total and white to even. The important thing is they all agree which color means which odd/even parity. Following either strategy will result in the second to tenth logicians to act all being correct and the first one having a 50% chance, so they will all live. This strategy will work for any number of logicians.
Axel and Bob each have his own 52-card deck. Both shuffle them randomly. They then turn over one card at a time, simultaneously, from each deck. What is the probability that they turn over the same card at the same time at least once?
It would be easily to estimate the answer as 1-(51/52)52 = 0.63568648. However, estimates are so intellectually unsatisfying. So, let's find an exact solution!
Step 1: To start, consider the number of ways the second deck can be ordered where the first card is number 1. The answer is the number of ways to order the other 51 cards, which is 51! = 1551118753287382280224243016469303211063259720016986112000000000000.
Any card can match the first deck, so we must do this for all 52 cards. This gives us 52*51! = 52! combinations where at least one card matches.
Step 2: However, step 1 double counts every situation where two cards match. For example, if the first two cards were 1 and 2, we would have counted the 50! ways to arrange the other cards twice, once for 1 as the first card and a second time for 2 as the second card. The number of ways to choose 2 cards out of 52 is combin(52,2) = 1326. For each combination of two cards, there are 50! = 30414093201713378043612608166064768844377641568960512000000000000 ways to order the other cards. Thus, for step 2 we need to subtract out combin(52,2)*50! = (52*51/2!)*50! = 52!/2! combinations.
Step 3: Next, consider the situation where the first three cards in the random deck are 1, 2, and 3 in order. There are 49! ways to order the other 49 cards. We would have counted them three times in the initial step of counting for at least one matching card. Then we would have subtracted out all combin(3,2)=3 ways to choose 2 out of these three cards in the second step. So this situation would have been counted 3-3=0 times, so we need to add them back in. There are combin(52,3) such situations of choosing at least 3 cards that match. So we need to add back in combin(52,3)*49! = 52*51*50*49!/3! = 52!/3! combinations back in.
Step 4: Next, consider the situation where the first four cards in the random deck are 1, 2, 3, and 4 in order. There are 48! ways to order the other 48 cards. We would have counted them four times in the initial step of counting for at least one matching card. Then we would have subtracted out all combin(4,2)=6 ways to choose two out of these four cards in step 2. Then we would have added all combin(4,3)=4 ways to choose 3 out of these four cards. So we are at 4-6+4=2 ways each such situation would have been counted. So we need to subtract one of those ways out, so that each situation will be counted once. There are combin(52,4)*48! = 52*51*50*49*48!/4! = 52!/4! such situations that need to be added back in.
We will keep doing this, alternating adding and subtracting to correct for double counting.
In the end, the number of situations where at least one card in the random deck matches the ordered deck = combin(52,1)*51! - combin(52,2)*50! + combin(52,3)*49! - combin(52,4)*48! ... - combin(52,52)*1! = 52!/1! - 52!/2! + 52!/3! - 52!/4! ... - 52!/52! = x = 333239808909468890675694068318655265019682314241643033726180828783.
There are 52! = y = 527177615496365219422618541545122659969212453861982208000000000000 total ways to order 52 cards.
Thus, the answer is x/y = 0.6321205588285576784044762298
The probability that there are no matches is 1-(x/y) = 0.3678794411714423215955237702.
If this number looks familiar, it should. 1/e = 0.3678794411714423215955237702.
So, the answer can be VERY closely estimated as 1-(1/e).
Acknowledgements
Mathematical calculations were done in Pari/GP
This problems was asked and discussed in my forum at Wizard of Vegas.
A circle of radius 1 is tangent to a parabola of equation y=x2. What is the area of the region in red, between the circle and parabola?
Click the button below for the answer.
Here is my solution. (PDF)
This question is asked and discussed in my forum at Wizard of Vegas.
I got this problem from Presh Talwalker of Mind Your Decisions.
A casino dealer is working on a new Three Card Poker variant. She takes all the face cards from a standard deck and thoroughly shuffles them. She then deals 3 cards to Player #1, three cards to Player #2, three cards to Player #3, and the final three cards to Player #4. What is the probability that all four hands will contain a straight (J-Q-K of any suit)?

The probability the first hand is A-K-Q is 1*(8/11)*(4/10) = 29.09%.
The probability the second hand is A-K-Q, given the first already is, equals 1*(6/8)*(3/7) = 32.14%.
The probability the third hand is A-K-Q, given the first and second already are, equals 1*(4/5)*(2/4) = 40.00%
The cards left must be A-K-Q, given the first three hands are. Thus, the probability is the product of the three above probabilities, which is 216/5775 = apx. 0.037402597.
This question is asked and discussed in my forum at Wizard of Vegas.
What is the average area and perimeter of a rectangle randomly inscribed in a circle of radius 1?
Good question. Here are my answers:
Here is my solution to both (PDF).
Find a ten-digit number such that:
- The first digit of the number is the number of 0's in the entire number.
- The second digit of the number is the number of 1's in the entire number.
- The third digit of the number is the number of 2's in the entire number.
- The 4th digit of the number is the number of 3's in the entire number.
- The 5th digit of the number is the number of 4's in the entire number.
- The 6th digit of the number is the number of 5's in the entire number.
- The 7th digit of the number is the number of 6's in the entire number.
- The 8th digit of the number is the number of 7's in the entire number.
- The 9th digit of the number is the number of 8's in the entire number.
- The 10th digit of the number is the number of 9's in the entire number.
This question is asked and discussed in my forum at Wizard of Vegas.
Three points are distributed randomly and uniformly along a circle with radius 1. What is the expected minimum distance between the three points, where distances are measured along the circumference?
Here is my solution (PDF).
This question is asked and discussed in my forum at Wizard of Vegas.
It takes Alice and Bill 3 hours to paint a house.
It takes Alice and Cindy 4 hours to paint a house.
It takes Bill and Cindy 5 hours to paint a house.
How long does it take if they all paint?




